A block A of mass m1 rests on a horizontal table. A light string connected to it passes over a frictionless pulley at the edge of table and from its other end another block B of mass m2 is suspended. The coefficient of kinetic friction between the block and the table isμk. When the block A is sliding on the table the tension in the string is
(m2+μkm1)g(m1+m2)
(m2−μkm1)g(m1+m2)
m1m2(1+μk)g(m1+m2)
m1m2(1−μk)g(m1+m2)
The correct Answer is:C
Frictional force acting on block A = μkm1g
Hence resultant force on the blocks = m2g−μkm1g
Their acceleration, a = m2g−μkm1gm1+m2
If the tension in the string is T, then for block B,
m2g−T=m2a
∴T=m2(g−a)=m2g(1−m2−μkm1m1+m2)
=m2g(m1+μkm1)m1+m2
=m1m2(1+μk)gm1+m2

Topper's Solved these Questions
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - EXAMINATION ARCHIVE with solutions (WBJEE )
3 Videos
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - EXAMINATION ARCHIVE with solutions ( JEE Main )
2 Videos
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - ENTRANCE CORNER ( Integer answer type )
1 Videos
- FIRST AND SECOND LAW OF THERMODYNAMICSBOOK - CHHAYA PUBLICATIONCHAPTER - FIRST AND SECOND LAW OF THERMODYNAMICSEXERCISE - CBSE SCANNER
18 Videos
- HYDROSTATICSBOOK - CHHAYA PUBLICATIONCHAPTER - HYDROSTATICSEXERCISE - CBSE SCANNER
1 Videos
Similar Questions
A block A of mass m1 rests on a horizontal table. A light string connected to it passes over a frictionless pulley at the edge of table and from its other end another block B of mass m2 is suspended. The coefficient of knetic friction between the block and table is μk . When the block A is sliding on the table, the tension in the string is.
View SolutionA block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
View Solution
Knowledge Check
A block A of mass m1 rests on a horizontal table. A light string connected to it passes over a frictionless pulley at the edge of table and from its other end another block B of mass m2 is suspended. The coefficient of knetic friction between the block and table is μk . When the block A is sliding on the table, the tension in the string is.
A(m2+μkm1)gm1+m2B(m2−μkm1)gm1+m2Cm1m2(1+μk)g(m1+m2)Dm1m2(1−μk)g(m1+m2)A block A of mass m1 rests on a horizontal table. A light string connected to it passes over a frictionless pully at the edge of the table and from its other end another block B of mass m2 is suspended. The coefficient of kinetic friction between the block and the table is H. When the block A is sliding on the table, the tension in the string is
Am1m2(1+μk)g(m1+m2)Bm1m2(1−μk)g(m1)+m2C(m2+μkm1)g(m1+m2)D(m2−μkm1)g(m1+m2)A block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
Am2gm1+m2Bm1gm1+m2CgDm2gm1
A body of mass 20 kg is resting on a table. A light string is attached to it and passed over a smooth pulley at the edge of the table and a mass 3kg is attached at the free end. What is the acceleration of the system of the coefficient of kinetic friction between the mass and the table is 0.04 ? What is the tension in the string ?
View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionA block A of mass m1 is placed on a horizontal frictionless table. It is connected to one end of a light spring of force constant k whose other end is fixed to a wall. A small block B of mass m2 is placed on block A. The coefficient of static friction between the blocks is μ. The system is displaced slightly from its equilibrium position and released. What is the maximum amplitude of the resulting simple harmonic motion of the system so that the upper block does not slip over the lower block ?
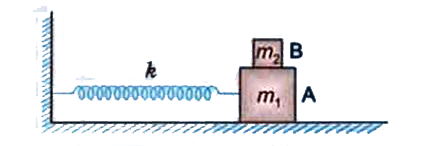
View SolutionA block of mass m1 rests on a rough horizontal plane with coefficient of friction as μ. A light strin attached to this block passes over a light frictionless pulley and carries another block of mass m2 as shown in figure. If the system is just about to move, then find the value of μ.
View Solution
