
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will be
x√m2k
x√2km
x√mk
x2km
The correct Answer is:B
(b) 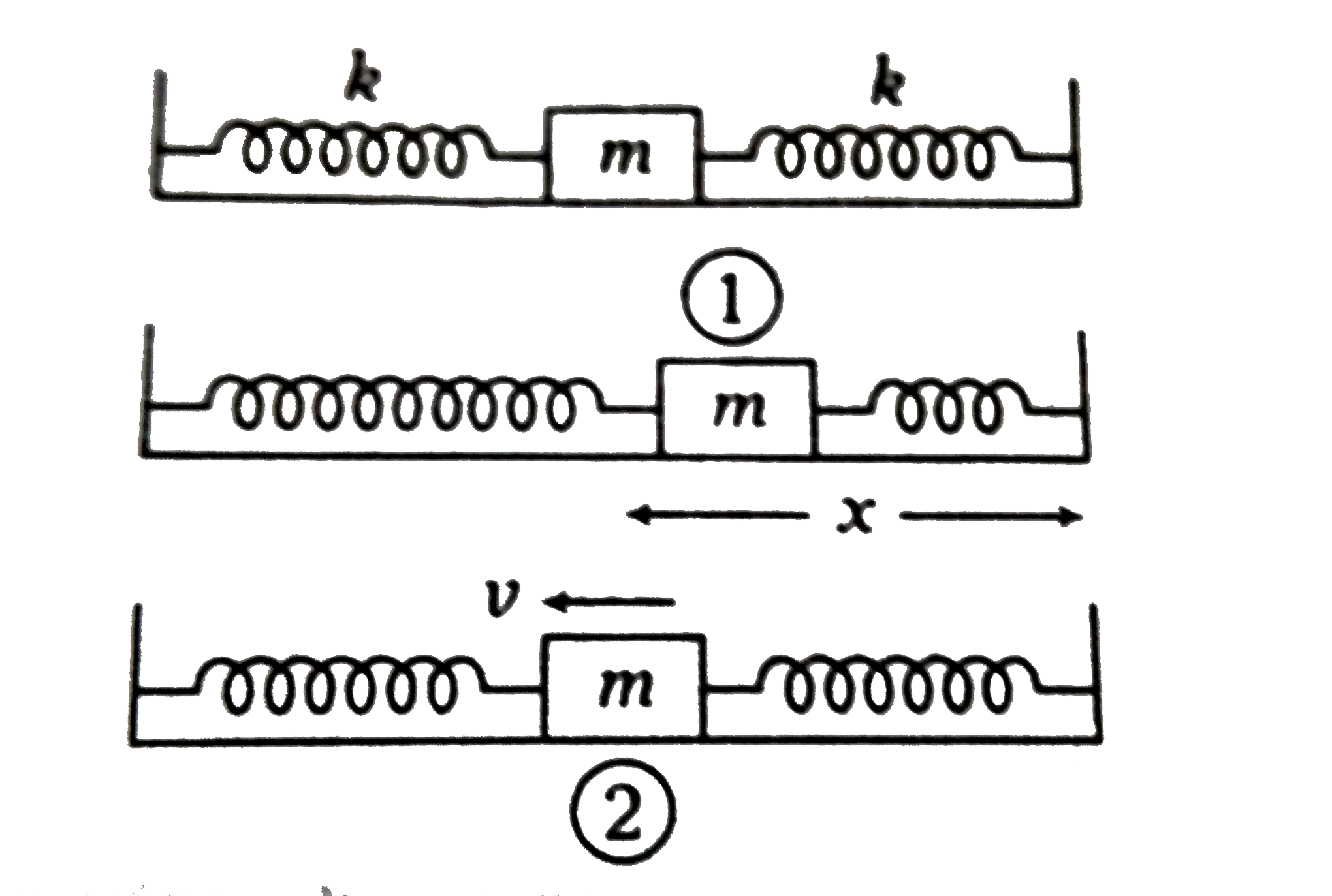
Total QE of spring =Total KE of block
12kx2+12kx2=12mv2
kx2=12mv2⇒v=√2kmx
Wf=loss in mechanical energy
μmgd=mgd⇒d=5m.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRANCE SPECIAL QUESTIONS
16 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - MATCH THE COLUMNS
7 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.3
10 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEYCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
Similar Questions
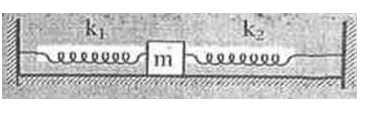
A block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.

View SolutionA block of mass m is attached to two unstretched springs of spring constant k1 and k2 as shown in figure. The block is displaced towards right through a distance 'x' and is released. Find the speed of the block as it passes through a distance x/4 from its mean position. All the surfaces are smooth.
View Solution
Knowledge Check
A block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.
 A√k1+k2mxB√k1k2m(k1+k2)xC ⎷k21k22m(k21+k22)xD ⎷k31k32m(k31+k32)
A√k1+k2mxB√k1k2m(k1+k2)xC ⎷k21k22m(k21+k22)xD ⎷k31k32m(k31+k32)A block of mass m is attached to four unstretched massless springs of spring constant k1andk2 as shown in figure. The block is displaced towards right through distance x and is released. Speed of block when displacement of block is x/2 from mean position is :
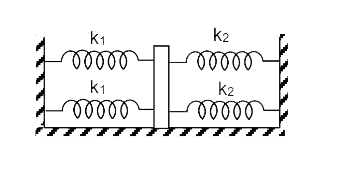 A√2(k1+k2)xmB√3(k1+k2)x22mC√(k1k2)3(k1+k2)mD√(k1+k2)x(k1+k2)m
A√2(k1+k2)xmB√3(k1+k2)x22mC√(k1k2)3(k1+k2)mD√(k1+k2)x(k1+k2)mA 10 kg metal block is attached to a spring constant 1000Nm−1. A block is displaced from equilibrium position by 10 cm and released. The maximum acceleration of the block is
A10ms−2B100ms−2C200ms−2D0.1ms−2
A block of mass m = 2 kg is attached to two unstretched spring of force constant k1=100N/m and k2=125N/m
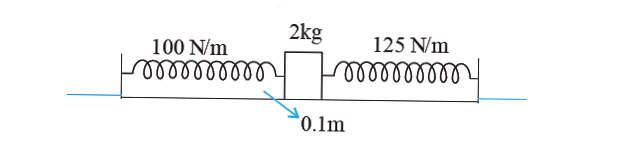
The block is displaced towards left through a distance of 10 cm and released. Find the speed of the block as it passes through the mean position.
View SolutionA sping of spring constant k is attached to the ceiling. A block of mass M is attached to its lower end and is released suddenly.
(ii) Find its speed at the instant it passes throught the equilibrium position.
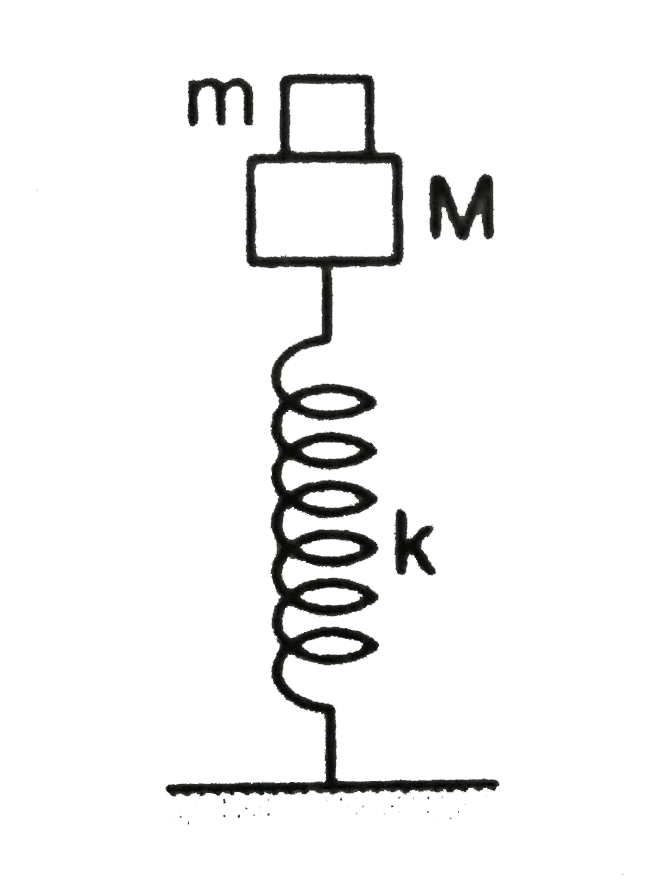
View SolutionA small block of mass m is kept on a bigger block of mass M which is attached to a vertical spring of spring constant k as shown in the figure. The system oscilates verticaly. a.Find the resultant force on the smaller block when it is displaced through a distance x above its equilibrium position. b. find the normal force on the smaller blok at this position. When is this force smallest smaller block at this position. When is this force smallest in magnitude? c. What can be the maximum amplitude with which the two blocks may oscillate together?
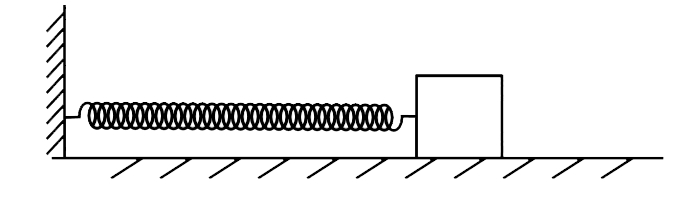
View SolutionA spring block system is placed on a rough horizontal floor. Force constant of the spring is k. The block is pulled to right to give the spring an elongation equal to x0 and then it is released. The block moves to left and stops at the position where the spring is relaxed. Calculate the maximum kinetic energy of the block during its motion.
View SolutionA block of mass m is attached to a spring of force constant k .Charges on the block is q. A horizontal electric field E is acting in the directions as shown.Block is released with the spring in unstretched position

block will execute SHM
(b) time period of osciallation is 2π√mk
(c) amplitude of oscillation is qEk
Block will oscillate but not simple harmonically
choose the correct answer
View Solution
