A block of mass $m$ is kept on the edge of a horizontal turn table of radius $R$ which is rotating with constant angular verticle $ω$ (along with the block ) about its axis . If coefficient of friction is $μ$ , find the friction force between block and table.

Video Solution

Text Solution

Verified by Experts

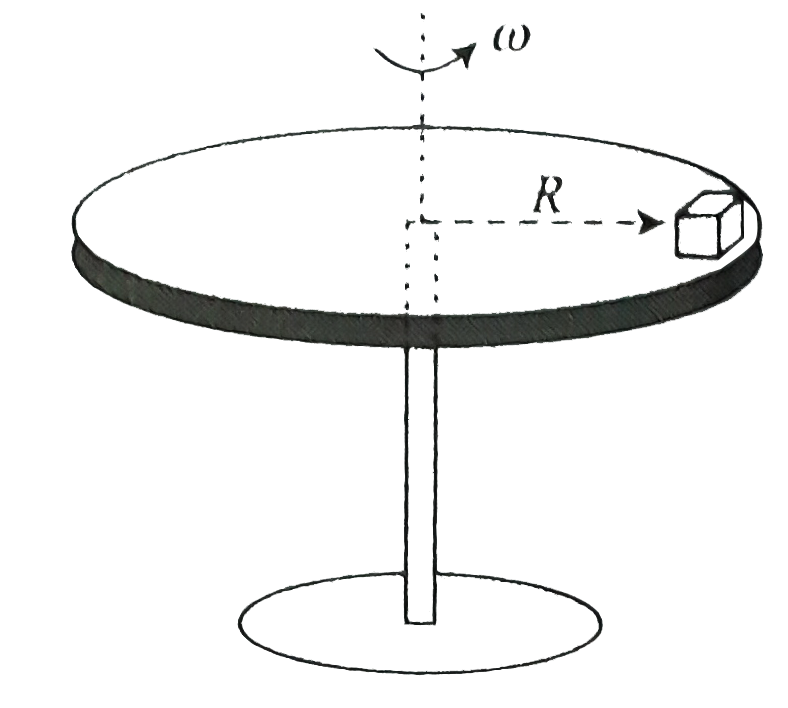
The block in Fig does not accelerate vertically. Therefore , we model it as a particle in equilibrum in the verticle direction if centripetal acceleration in the horizontal direction in this case centriprted is proveded by friction.

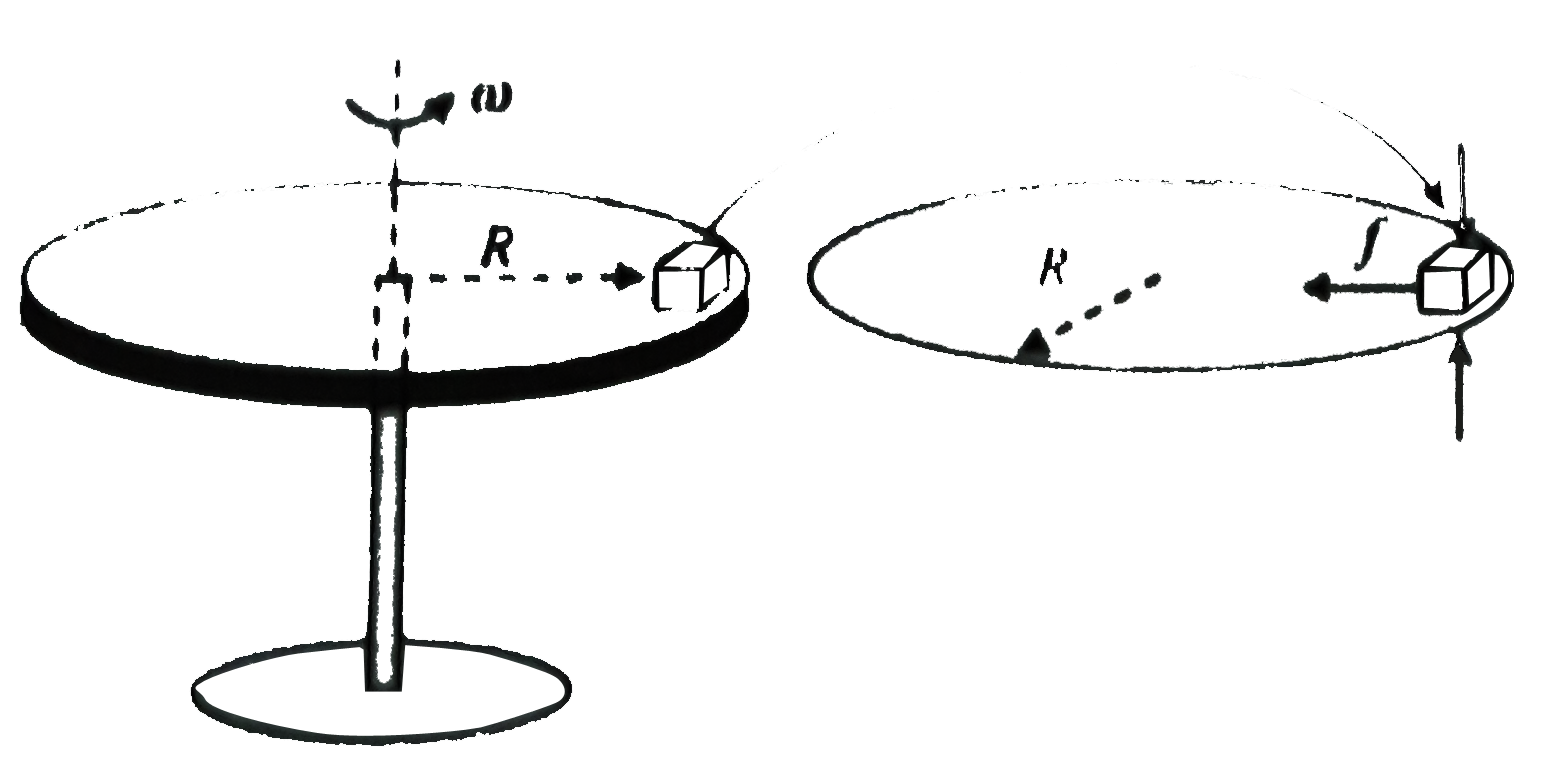
$\sum F_{y} = N - m g = 0$ ...(i)
$N = m g$ ....(ii)
$\sum F_{x} = f = m a_{c} = m ω^{2} R$
Friction force = centripental force $= m ω^{2} R$

|

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If coefficient of friction between both the block is $μ - \frac{1}{2}$ . Find friction force acting between both block.

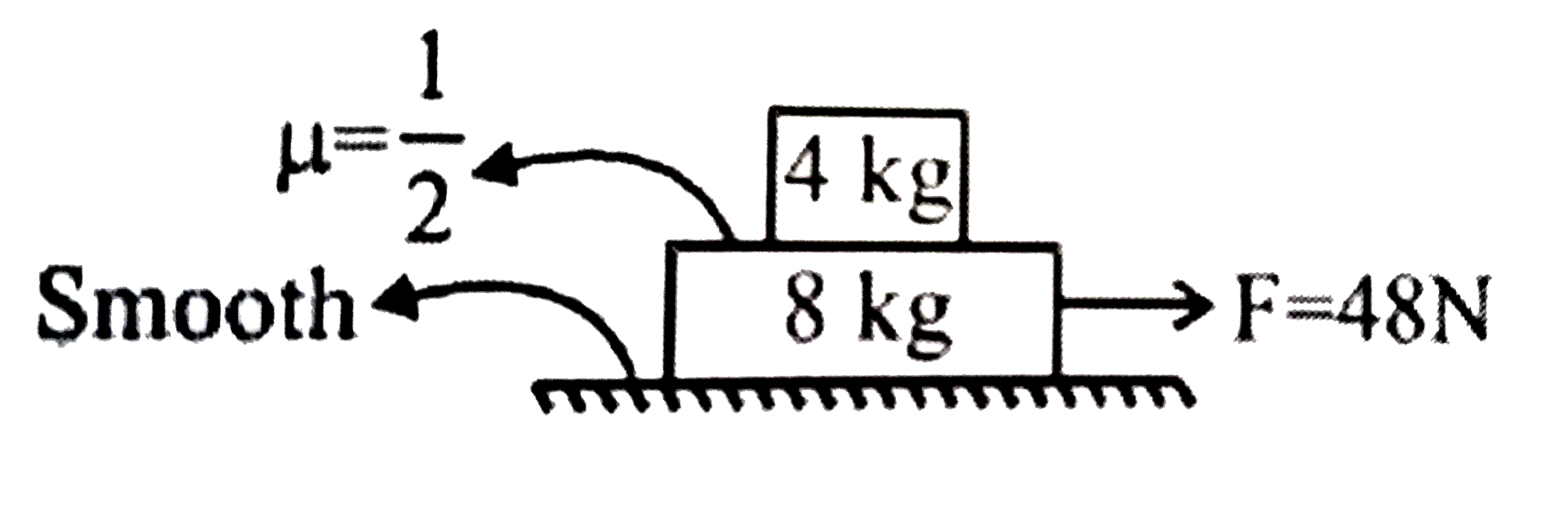A $16 N$
B $20 N$
C $8 N$
D $10 N$
Question 2 - Select One
A ring of radius $R$ is rotating with an angular speed $ω_{0}$ about a horizontal axis. It is placed on a rough horizontal table. The coefficient of kinetic friction is $μ_{k}$ . The time after it starts rolling is.
A $\frac{ω_{0} μ_{k} R}{2 g}$
B $\frac{ω_{0} g}{2 μ_{k} R}$
C $\frac{2 ω_{0} R}{μ_{k} g}$
D $\frac{ω_{0} R}{2 μ_{k} g}$
Question 3 - Select One
A block A of mass $m_{1}$ rests on a horizontal table. A light string connected to it passes over a frictionless pully at the edge of the table and from its other end another block B of mass m2 is suspended. The coefficient of kinetic friction between the block and the table is H. When the block A is sliding on the table, the tension in the string is
A $\frac{m_{1} m_{2} (1 + μ_{k}) g}{(m_{1} + m_{2})}$
B $\frac{m_{1} m_{2} (1 - μ_{k}) g}{(m_{1}) + m_{2}}$
C $\frac{(m_{2} + μ_{k} m_{1}) g}{(m_{1} + m_{2})}$
D $\frac{(m_{2} - μ_{k} m_{1}) g}{(m_{1} + m_{2})}$

CENGAGE PHYSICS-NEWTON'S LAWS OF MOTION 2-Integer type

Home
Ask Doubt
Profile