A block of mass m is sliding down a stationary inclined plane. The base of the inclined plane has a length l, and the coefficient of kinetic friction between the block and inclined surface is 0.14. What should be the inclination of the plane so that the block can slide down to the ground in minimum time?
Acceleration of the block along the plane ,
a = g (sin θ−μ.cosθ )
Let the time required to slide down from A to B be t Fig.
∴AB=12at2=lcosθ
or, 12t2g(sinθ−μ.cosθ)=lcosθ
or, t2=2lg1sinθcosθ−μ.cos2θ
=4lg[1sin2θcosθ−μ.(1+cos2θ)]
When t is minimum t2 is also minimum.
∴sin2θi−μ(1+cos2θ) = x (say)is maximum.
∴dxdθ=0 or,2cos2θ−μ.(0−2sin2θ) =0
or, cos 2 θ+μsin2θ =0
or , tan2θ=−1μ.=−10.14=−tan82∘
or, tan2θ=tan(180∘−82∘)=tan98∘
∴2θ=98∘andθ=49∘.

Topper's Solved these Questions
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - Section Related Questions
9 Videos
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - HIGHER ORDER THINKING SKILL ( HOTS ) QUESTIONS
14 Videos
- FIRST AND SECOND LAW OF THERMODYNAMICSBOOK - CHHAYA PUBLICATIONCHAPTER - FIRST AND SECOND LAW OF THERMODYNAMICSEXERCISE - CBSE SCANNER
18 Videos
- HYDROSTATICSBOOK - CHHAYA PUBLICATIONCHAPTER - HYDROSTATICSEXERCISE - CBSE SCANNER
1 Videos
Similar Questions
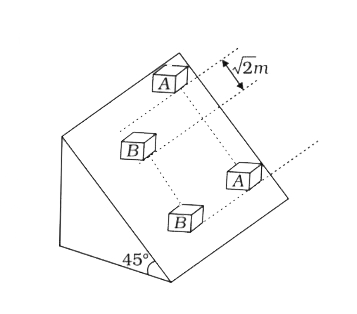
Two identical blocks A and B of equal masses are placed on rough inclined plane as shown in the figure. Initially the block A is √2m behind the block B. Coefficient of kinetic friction for the blocks A and B are 0.2 and 0.3 respectively (g=10m/s2). By the time the two blocks come on the same line on the inclined plane if they are released simultaneously, the distance moved by B is βm Find the value of β
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View Solution
Knowledge Check
A block sliding down on a rough 45∘ inclined plane has half the velocity it would have been, the inclined plane is smooth. The coefficient of sliding friction between the block and the inclined plane is
A14B34C12√2D1√2A block sliding down on a rough 45∘ inclined planes has half the velocity it would have been, the inclined plane is smooth. The coefficient of sliding friction between the the block and the inclined plane is
A14B34C12√2D1√2A block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
A block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block slides down a curved frictionless track and then up an inclined plane as in figure. The coefficient of kinetic friction between the block and incline is μk. Find the maximum height reached by the block.

View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block of mass mm remains stationary on a fixed inclined plane of inclination θ . If μ= coefficient of static friction the reaction of ground on the block is:
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View Solution
