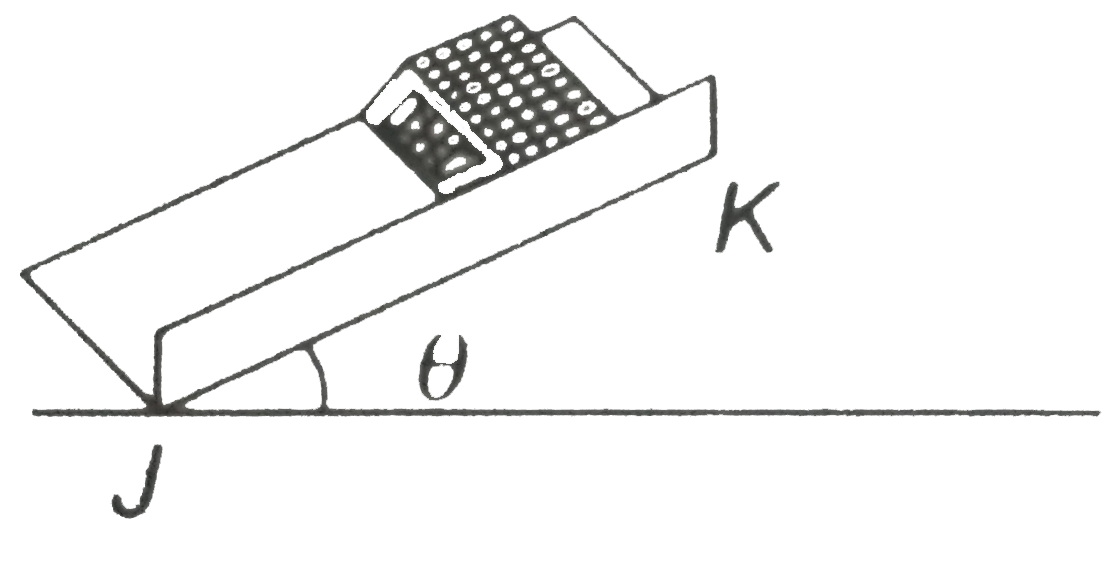
A block of mass m sides down an inclined right angled trough .If the coefficient of friction between block and the trough is μk acceleration of the block down the plane is

g(sinθ+√2μkcosθ)
g(sinθ+μkcosθ)
g(sinθ−√2μkcosθ)
g(sinθ−μkcosθ)
The correct Answer is:C
Resultant of N and N(=√2N) is equal to mgcosθ
∴√2N=mgcosθ
∴N=mgcosθ√2
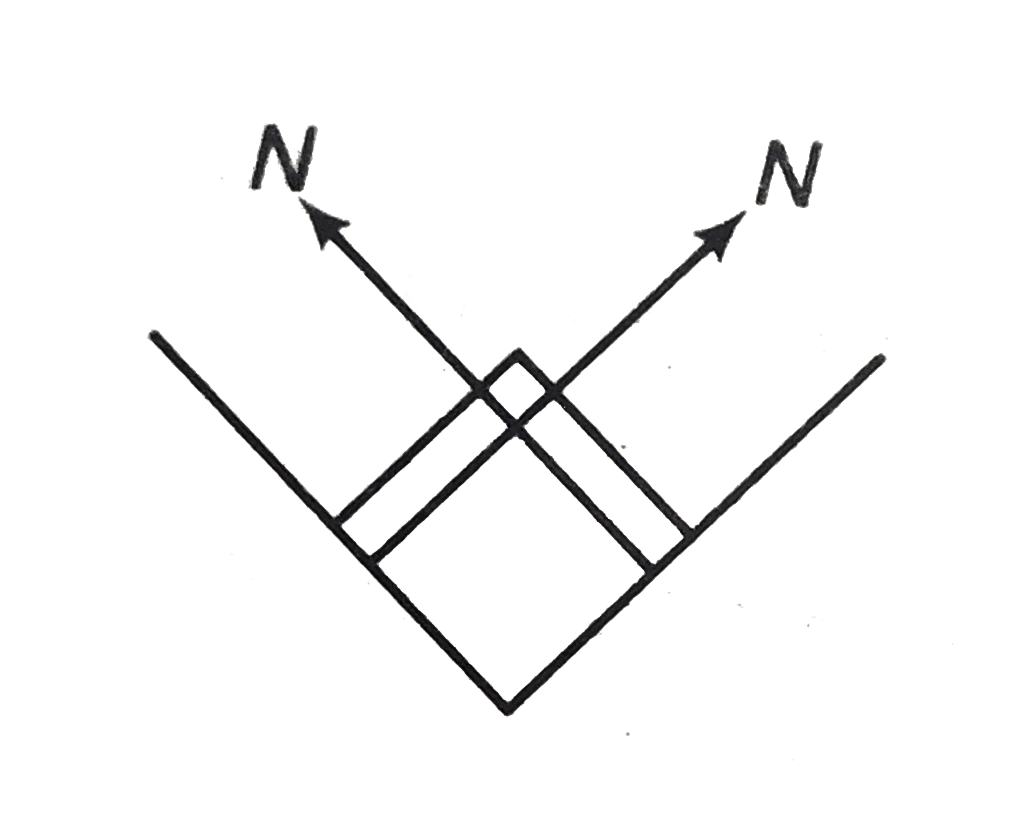
Now kinetic friction will act from two sides
∴a=mgcosθ−2μkNm
Subtituting the value of N, we get
a=g(sinθ−√2μkcosθ)
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Subjective Question
27 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Single Correct
90 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
Knowledge Check
A block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θA block of mass m is placed at rest on an inclination θ to the horizontal.If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
AmgBμmgcosθCmgsinθDμmgtanθA block of mass m is lying on an inclined plane. The coefficient of friction between the plane and the block is μ. The force (F1) required to move the block up the inclined plane will be:-
Amgsinθ+μmgcosθBmgcosθ−μmgsinθCmgsinθ−μmgcosθDmgcosθ+μmgsinθ
A block of mass m slides down an inclined plane of inclination θ with uniform speed The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is .
View SolutionA block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?
View SolutionA block of mass 10 kg is placed in a car going down an incline of inclination 60∘. If the coefficient of friction between the block and car floor is 1√3. Find the acceleration a of car down the inline so that the block does't slip on the car surface.
View Solution