A body is moving along the +ve X-axis with uniform acceleration of −4ms2 Its velocity at x = 0 is 10ms−1. The time taken by the body to reach a point at x = 12m is
(25, 3s)
(38, 4s)
(48,8s)
(1s, 28)
The correct Answer is:A
To solve the problem step by step, we will use the kinematic equation for uniformly accelerated motion:
Step 1: Identify the given values
- Initial velocity (u) = 10 m/s (at x = 0)
- Acceleration (a) = -4 m/s² (uniform acceleration)
- Displacement (s) = 12 m (the point we want to reach)
Step 2: Write the kinematic equation
The kinematic equation we will use is:
s=ut+12at2
Step 3: Substitute the known values into the equation
Substituting the values we have:
12=10t+12(−4)t2
Step 4: Simplify the equation
This simplifies to:
12=10t−2t2
Rearranging gives:
2t2−10t+12=0
Step 5: Divide the entire equation by 2
To make calculations easier, divide the entire equation by 2:
t2−5t+6=0
Step 6: Factor the quadratic equation
Now, we need to factor the quadratic equation:
(t−2)(t−3)=0
Step 7: Solve for t
Setting each factor to zero gives us:
1. t−2=0 → t=2 seconds
2. t−3=0 → t=3 seconds
Step 8: Conclusion
The time taken by the body to reach the point at x = 12 m is either 2 seconds or 3 seconds.
- Initial velocity (u) = 10 m/s (at x = 0)
- Acceleration (a) = -4 m/s² (uniform acceleration)
- Displacement (s) = 12 m (the point we want to reach)
The kinematic equation we will use is:
s=ut+12at2
Substituting the values we have:
12=10t+12(−4)t2
This simplifies to:
12=10t−2t2
2t2−10t+12=0
To make calculations easier, divide the entire equation by 2:
t2−5t+6=0
Now, we need to factor the quadratic equation:
(t−2)(t−3)=0
Setting each factor to zero gives us:
1. t−2=0 → t=2 seconds
2. t−3=0 → t=3 seconds
The time taken by the body to reach the point at x = 12 m is either 2 seconds or 3 seconds.
Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A PLANE
87 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
Similar Questions
A body of mass 2kg starts from rest and moves with uniform acceleration. It acquires a velocity 20ms−1 in 4s.
The power exerted on the body at 2s is
View SolutionThe initial velocity of a body moving along a straight lines is 7m/s. It has a uniform acceleration of 4m/s2 the distance covered by the body in the 5th second of its motion is-
View SolutionIf v is the velocity of a body moving along x-axis, then acceleration of body is
View SolutionThe average velocity of a body moving with uniform acceleration after travelling a distance of 3.06m is 0.34ms−1. If the change in velocity of the body is 0.18ms−1 during this time, its uniform acceleration is .
View SolutionVelocity of a body moving a straight line with uniform acceleration (a) reduces by 34 of its initial velocity in time t0. The total time of motion of the body till its velocity becomes zero is
View SolutionA particle moving with uniform acceleration has its final velocity (v=√150+8x) m/s where x is the distance travelled by the body. Then the acceleration is
View SolutionA particle is moving along the x-axis with an acceleration a = 2x where a is in ms–2andx is in metre. If the particle starts from rest at x=1 m, find its velocity when it reaches the position x = 3.
View SolutionA body of mass 2kg starts from rest and moves with uniform acceleration. It acquires a velocity 20ms−1 in 4s.
Find average power transferred to the body in first 2s.
View SolutionFor a body travelling with uniform acceleration, its final velocity is v=√180−7x , where x is the distance travelled by the body. Then the acceleration is
View SolutionThe acceleration of a particle which moves along the positive x-axis varies with its position as shown in figure. If the velocity of the particle is 0.8ms−1 at x = 0, then velocity of the particle at x=1.4m is (∈ms−1).
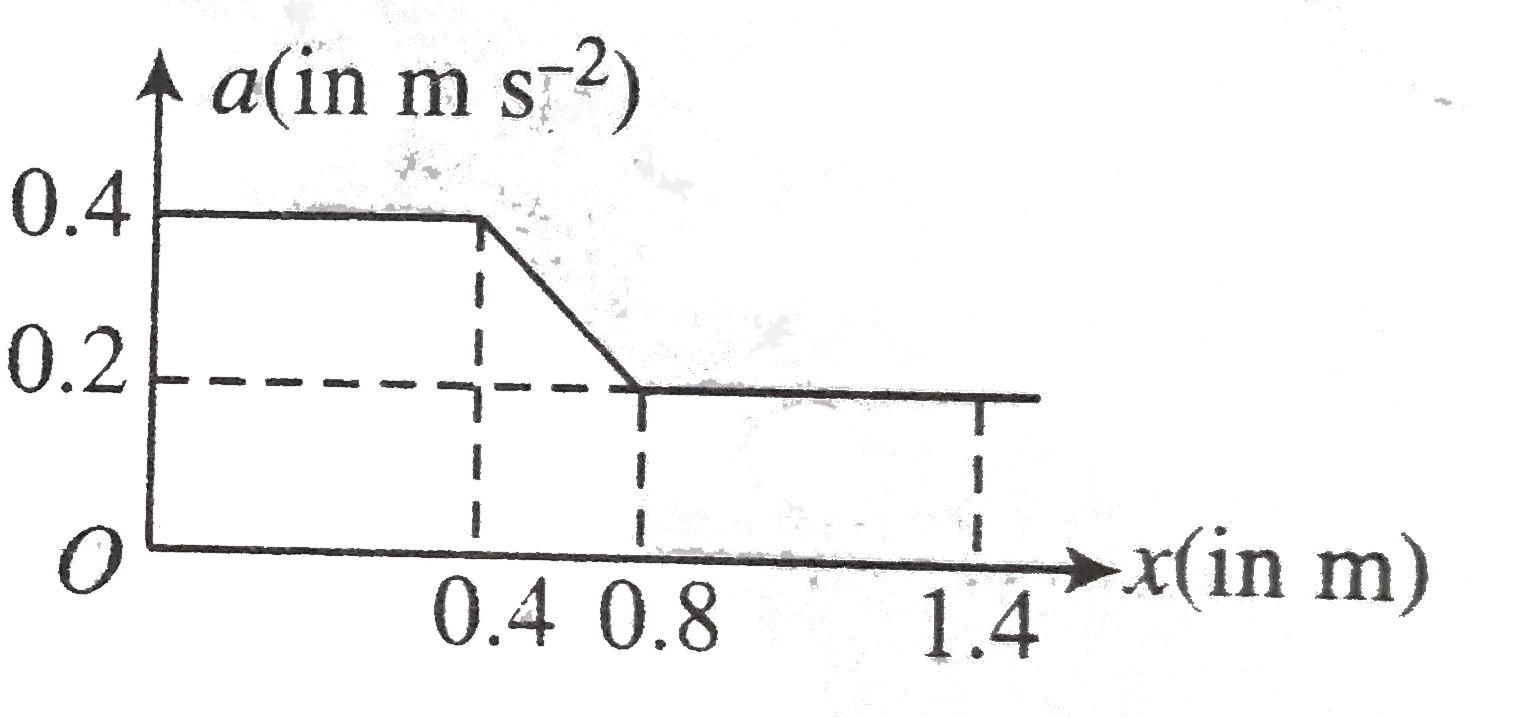
View Solution
