A body of mass m is tied to one end of a spring and whirled round in a horizontal circle with a constant angular velocity .The elongation is 1 cm . If the angular velocity is doubled , the elongation in the spring is 5 cm. what is the original length of the spring ?

A

13 cm

B

14 cm

C

15 cm

D

16 cm

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:C

To solve the problem, we need to analyze the forces acting on the mass tied to the spring when it is whirled in a horizontal circle. We will set up equations based on the elongation of the spring and the forces involved.
1. Identify the Variables:
- Let the original length of the spring be $L_{0}$ .
- The elongation when the angular velocity is $ω$ is $Δ L_{1} = 1 cm = 0.01 m$ .
- The elongation when the angular velocity is doubled $(2 ω)$ is $Δ L_{2} = 5 cm = 0.05 m$ .
2. Determine the Total Lengths:
- When the angular velocity is $ω$ :
$r_{1} = L_{0} + Δ L_{1} = L_{0} + 0.01$
- When the angular velocity is $2 ω$ :
$r_{2} = L_{0} + Δ L_{2} = L_{0} + 0.05$
3. Set Up the Force Equations:
- The centrifugal force acting on the mass is given by:
$F_{c} = m r ω^{2}$
- The spring force is given by Hooke's law:
$F_{s} = k Δ L$
- For the first case:
$m (L_{0} + 0.01) ω^{2} = k (0.01)$
- For the second case:
$m (L_{0} + 0.05) (2 ω)^{2} = k (0.05)$
4. Simplify the Equations:
- From the first case:
$m (L_{0} + 0.01) ω^{2} = k (0.01) (1)$
- From the second case:
$m (L_{0} + 0.05) (4 ω^{2}) = k (0.05) (2)$
5. Express $k$ from Equation (1):
- Rearranging equation (1):
$k = \frac{m (L_{0} + 0.01) ω^{2}}{0.01}$
6. Substitute $k$ into Equation (2):
- Substitute $k$ from equation (1) into equation (2):
$m (L_{0} + 0.05) (4 ω^{2}) = \frac{m (L_{0} + 0.01) ω^{2}}{0.01} (0.05)$
- Cancel $m$ and $ω^{2}$ (assuming $m \neq 0$ and $ω \neq 0$ ):
$4 (L_{0} + 0.05) = \frac{(L_{0} + 0.01) (0.05)}{0.01}$
- Simplifying gives:
$4 (L_{0} + 0.05) = 5 (L_{0} + 0.01)$
7. Expand and Rearrange:
- Expanding both sides:
$4 L_{0} + 0.2 = 5 L_{0} + 0.05$
- Rearranging gives:
$5 L_{0} - 4 L_{0} = 0.2 - 0.05$
$L_{0} = 0.15 m = 15 cm$
Final Answer:
The original length of the spring $L_{0}$ is 15 cm.

Updated on:7/8/2024

|

Class 12 PHYSICS CIRCULAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

A stone is tied to one end of a steing and rotated in horizontal circle with a uniform angular velocity. The tension in the string is T, if the lrngth of the string is halved and its angular velocity is doubled , the tension in the string will be
A4 T
B $T / 2$
C $T / 4$
D2 T
Stone of mass 1 kg tied to the end of a string of length 1m , is whirled in horizontal circle with a uniform angular velocity $2 r a d s^{- 1}$ . The tension of the string is (in newton)
A2
B $\frac{1}{3}$
C $4$
D $\frac{1}{4}$
A small ball of mass $m$ suspended from the celling at a point $O$ by a thread of length $l$ moves along a horizontal circle with a constant angular velocity $ω$ .
.
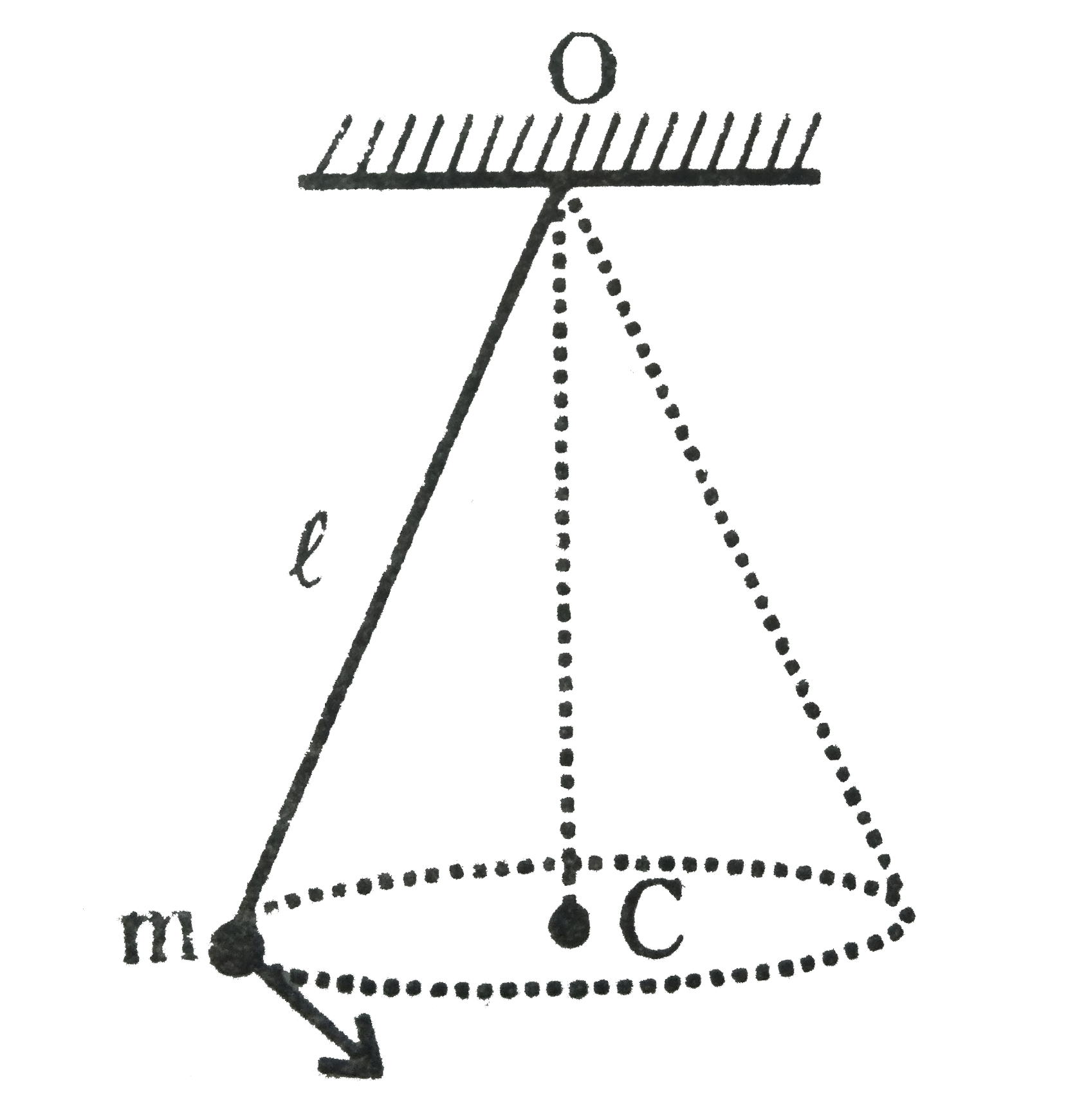Alinear momentum of system (ball + rod) is conserved
Bangular momentum about C is conserved
Ckinetic energy of system (ball + rod) before the collision is equal to kinetic energy of system just after the collision
Dlinear momentum of ball is conserved

MARVEL PUBLICATION-CIRCULAR MOTION-TEST YOUR GRASP-20

Home
Ask Doubt
Profile