A brass cube of side a and density σis floating in mercury of density ρ. If the cube is displaced a bit vertically, it executes S.H.M. Its time period will be
2π√σaρg
2π√ρaσg
2π√ρgσa
2π√σgρa
The correct Answer is:A
To solve the problem of finding the time period of a brass cube floating in mercury when it is displaced slightly, we can follow these steps:
1. Identify the Given Parameters:
- Side of the brass cube = a
- Density of brass = σ
- Density of mercury = ρ
2. Understand the Displacement:
- When the cube is displaced vertically by a small distance δx, it will experience a change in the buoyant force.
3. Calculate the Buoyant Force:
- The volume of the cube submerged in mercury when it is at equilibrium is equal to the volume of the cube, which is a3.
- The change in buoyant force ΔB when the cube is displaced by δx is given by:
ΔB=Area×Height×Density×g=a2⋅δx⋅ρ⋅g
- Thus, the change in buoyant force is:
ΔB=a2δxρg
4. Determine the Restoring Force:
- The restoring force FR acting on the cube is equal to the change in buoyant force:
FR=−ΔB=−a2δxρg
5. Relate the Restoring Force to SHM:
- According to Hooke's law for simple harmonic motion (SHM), the restoring force can be expressed as:
FR=−kδx
- Comparing both expressions gives:
k=a2ρg
6. Calculate the Mass of the Cube:
- The mass m of the brass cube is:
m=Density×Volume=σ⋅a3
7. Use the Formula for Time Period:
- The time period T of SHM is given by:
T=2π√mk
- Substituting the values of m and k:
T=2π√σa3a2ρg=2π√σaρg
8. Final Result:
- Therefore, the time period T of the brass cube executing SHM is:
T=2π√σaρg
- Side of the brass cube = a
- Density of brass = σ
- Density of mercury = ρ
- When the cube is displaced vertically by a small distance δx, it will experience a change in the buoyant force.
- The volume of the cube submerged in mercury when it is at equilibrium is equal to the volume of the cube, which is a3.
- The change in buoyant force ΔB when the cube is displaced by δx is given by:
ΔB=Area×Height×Density×g=a2⋅δx⋅ρ⋅g
- Thus, the change in buoyant force is:
ΔB=a2δxρg
- The restoring force FR acting on the cube is equal to the change in buoyant force:
FR=−ΔB=−a2δxρg
- According to Hooke's law for simple harmonic motion (SHM), the restoring force can be expressed as:
FR=−kδx
- Comparing both expressions gives:
k=a2ρg
- The mass m of the brass cube is:
m=Density×Volume=σ⋅a3
- The time period T of SHM is given by:
T=2π√mk
- Substituting the values of m and k:
T=2π√σa3a2ρg=2π√σaρg
- Therefore, the time period T of the brass cube executing SHM is:
T=2π√σaρg
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective type
3 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A solid cube of side a and density ρ0 floats on the surface of a liquid of density ρ. If the cube is slightly pushed downward, then it oscillates simple harmonically with a period of
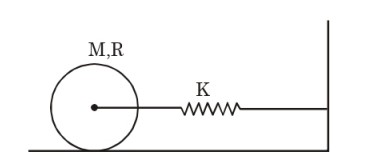
View SolutionA solid cylinder attached to horizontal massless spring can roll without slipping along a horizontal surface. Find time period of oscillation.
View SolutionA block of rectangular size of mass m and area of cross section A, float in a liquid of density ρ.If we give a small vertical displacement from equilibrium, It undergoes SHM with time period T, then
View SolutionA wooden cube of side 10 cm and density 0.8 gm/cm3 is floating in water (density =1 gm/cm3). A mass of (100x) gm is placed over the cube so that cube is completely immersed without wetting the mass. Find value of x.
View SolutionA cube of density 250 kg/m2 floats in water, then what part of total volume of the cube outside the water?
View SolutionA cubical block of wood of edge a and density ρ floats in water of density 2ρ. The lower surface of the cube just touches the free end of a mass less spring of force constant K fixed at the bottom of the vessel. The weight W put over the block so that it is completely immersed in water without wetting the weight is
View SolutionA cuboidal piece of wood has dimensions a, b and c. its relatively density is d. it is floating in a large body of water such that side a is vertical. It is pushed down a bit and released. The time period of SHM executed by it is
View SolutionAn object of mass m is floating in a liquid of density σ. If the object is made up of density ρ, then appare weight of the object in the liquid is
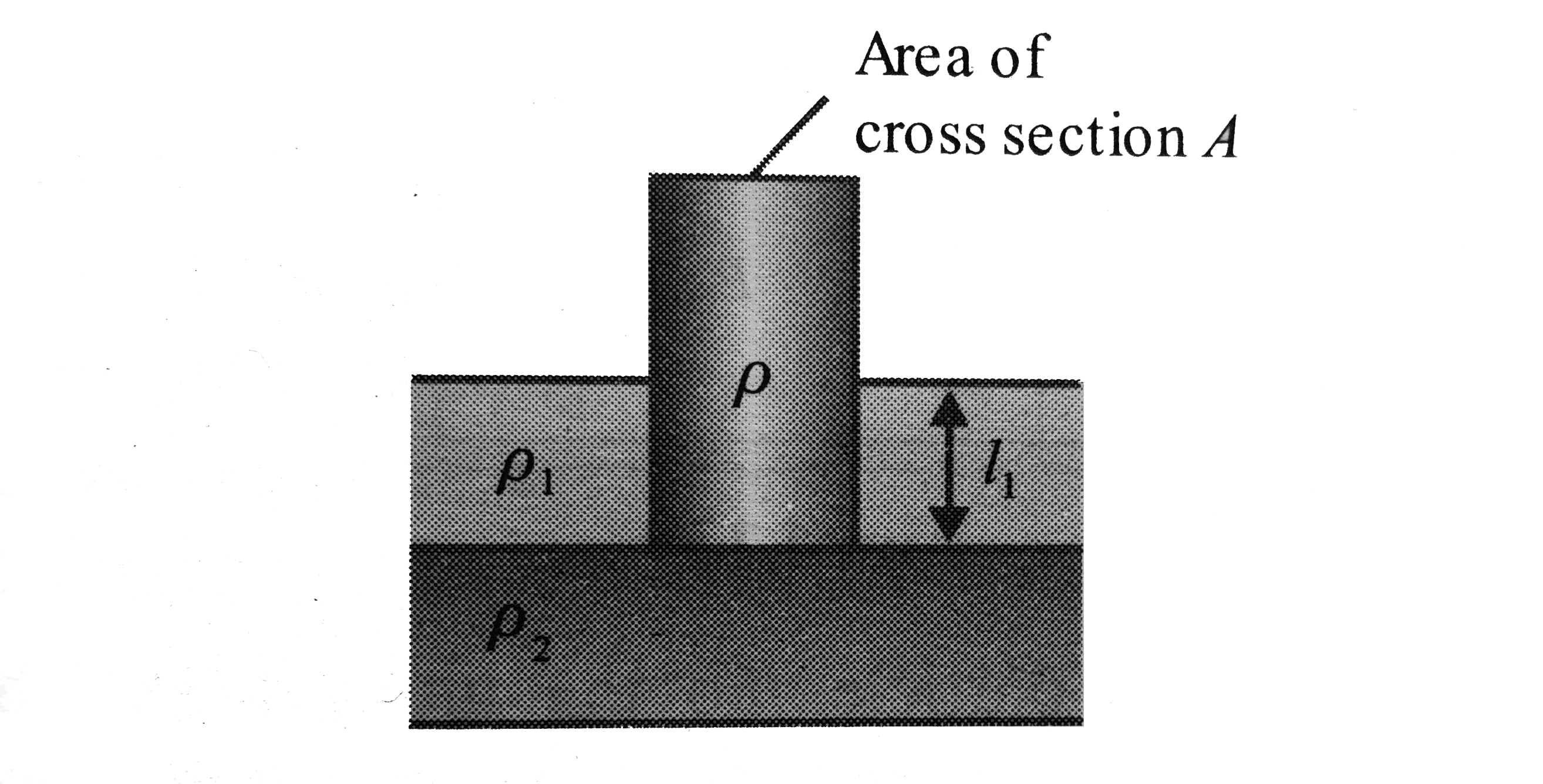
View SolutionA vertical pole of length l , density ρ , area of cross section A floats in two immiscible liquids of densities ρ1and ρ2. In equuilibrium possition the bottom end is at the interface of the liquids. When the cylinder is displaced vertically, find the time period of oscillation.
View SolutionA vertical U tube contains a liquid of density ρ, length of the liquid in the tube is 2H. The liquid is displaced slightly and released. Show that the liquid will execute SHM. Also find its time period. Take liquid to be ideal.

View Solution
