A bus is moving towards a gauge wall with a velocity of 5m/s−1. The driver sounds a horn of frequency 200Hz. The frequency of the beats heard by a passenger of the bus will be ………… Hz (Speed of sound in air =342m/s−1)
To solve the problem, we need to determine the frequency of the sound heard by a passenger in the bus when the bus is moving towards a wall while sounding a horn. We will use the Doppler effect formula for sound.
Step 1: Identify the given values
- Velocity of the bus (source), vs=5m/s
- Frequency of the horn (source frequency), fs=200Hz
- Speed of sound in air, v=342m/s
Step 2: Calculate the frequency of the sound heard by the wall
When the bus (source) moves towards a stationary wall (observer), the frequency observed by the wall can be calculated using the Doppler effect formula:
f′=fs(vv−vs)
Where:
- f′ = frequency heard by the wall
- fs = source frequency
- v = speed of sound
- vs = speed of the source
Substituting the values:
f′=200(342342−5)
Step 3: Simplify the expression
Calculate the denominator:
342−5=337
Now substitute back into the equation:
f′=200(342337)
Step 4: Calculate the frequency heard by the wall
Now, calculate 342337:
342337≈1.0148
Now multiply by 200 Hz:
f′≈200×1.0148≈202.96Hz
Step 5: Calculate the frequency of the beats heard by the passenger
The sound reflected from the wall will act as a new source of sound. The passenger in the bus will hear this reflected sound. The frequency of the sound heard by the passenger is calculated using the same Doppler effect formula, but now the wall acts as the source and the bus as the observer:
f′′=f′(v+vsv)
Where:
- f′′ = frequency heard by the passenger
- v+vs = speed of sound plus the speed of the bus
Substituting the values:
f′′=202.96(342+5342)
Calculate the numerator:
342+5=347
Now substitute back into the equation:
f′′=202.96(347342)
Step 6: Calculate the final frequency heard by the passenger
Calculate 347342:
347342≈1.0146
Now multiply by 202.96:
f′′≈202.96×1.0146≈205.93Hz
Step 7: Calculate the beat frequency
The beat frequency is the difference between the frequency of the horn and the frequency heard by the passenger:
Beat Frequency=|f′′−fs|=|205.93−200|≈5.93Hz
Final Answer
The frequency of the beats heard by a passenger of the bus will be approximately 5.93 Hz.
---
- Velocity of the bus (source), vs=5m/s
- Frequency of the horn (source frequency), fs=200Hz
- Speed of sound in air, v=342m/s
When the bus (source) moves towards a stationary wall (observer), the frequency observed by the wall can be calculated using the Doppler effect formula:
f′=fs(vv−vs)
Where:
- f′ = frequency heard by the wall
- fs = source frequency
- v = speed of sound
- vs = speed of the source
f′=200(342342−5)
Calculate the denominator:
342−5=337
Now substitute back into the equation:
f′=200(342337)
Now, calculate 342337:
342337≈1.0148
Now multiply by 200 Hz:
f′≈200×1.0148≈202.96Hz
The sound reflected from the wall will act as a new source of sound. The passenger in the bus will hear this reflected sound. The frequency of the sound heard by the passenger is calculated using the same Doppler effect formula, but now the wall acts as the source and the bus as the observer:
f′′=f′(v+vsv)
Where:
- f′′ = frequency heard by the passenger
- v+vs = speed of sound plus the speed of the bus
f′′=202.96(342+5342)
Calculate the numerator:
342+5=347
Now substitute back into the equation:
f′′=202.96(347342)
Calculate 347342:
347342≈1.0146
Now multiply by 202.96:
f′′≈202.96×1.0146≈205.93Hz
The beat frequency is the difference between the frequency of the horn and the frequency heard by the passenger:
Beat Frequency=|f′′−fs|=|205.93−200|≈5.93Hz
The frequency of the beats heard by a passenger of the bus will be approximately 5.93 Hz.
Topper's Solved these Questions
Similar Questions
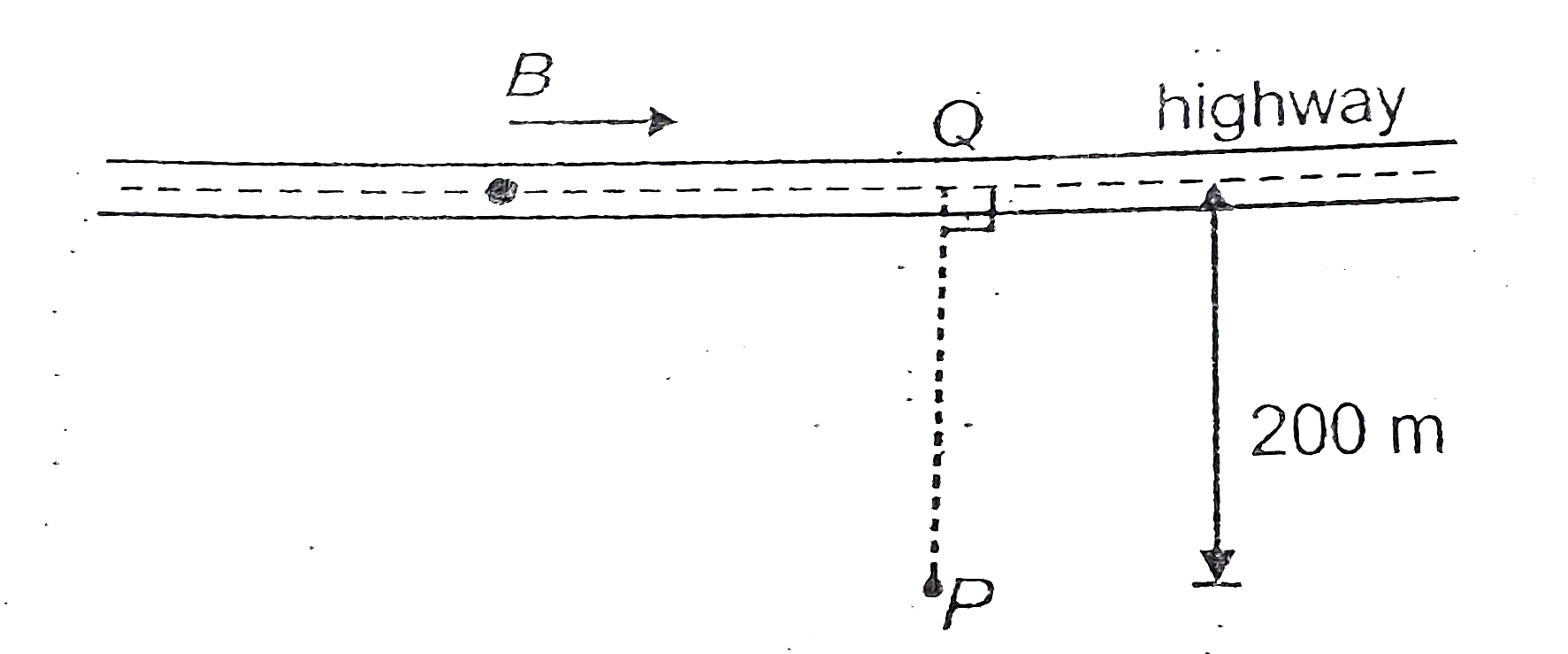
A person P is standing at a perpendicular distance of 200m from point Q on a highway. A bus B is moving with a speed of 42.43ms−1 towards point Q on the highway. The driver of the bus blows a horn of frequency 1300 Hz. What is the frequency of sound received by the person P, when the bus is distant 200 m from Q. speed of sound in air is 330ms−1
 View Solution
View SolutionA bus is moving with a velocity of 5ms−1 towards a huge wall. The driver sound a horn of frequency 165 Hz. If the speed of sound in air is 335ms−1, the number of beats heard per second by a passenger inside the bus will be
View Solution
Knowledge Check
- Question 1 - Select One
a bus is moving with a velocity 4 m/s towards a wall, the driver sounds a horn of frequency 173 Hz . if the speed of sound in air is 350 m/s. the number of beat heard per second by a passanger on the bus will be
AoneBtwoCthreeDfour - Question 2 - Select One
A bus is moving with a velocity of 5ms−1 towards a huge wall. The driver sound a horn of frequency 165 Hz. If the speed of sound in air is 335ms−1, the number of beats heard per second by a passenger inside the bus will be
A3B4C5D6 - Question 3 - Select One
a bus is moving in a circle around a listener with speed 20 m/s of radius 2 m. Bus driver blows a horn with frequency 210 Hz. the frequency of sound heard by the listener is
A212 HzB210 HzC218 HzD420 Hz
Two trains are moving towards each other at speeds of 20 m/s and 15 m/s relative to the ground. The first train sounds a whistle of frequency 600 Hz . the frequency of the whistle heard by a passenger in the second train before the train meets is (the speed of sound in air is 340 m/s )
View SolutionA car is moving with 90kmh−1 blows a horn of 150 Hz, towards a cliff. The frequency of the reflected sound heard by the driver will be (speed of sound in air is 340ms−1 )
View SolutionA car is moving with a velocity of 5m/s towards huge wall. The driver sounds a horn of frequency 165Hz. If the speed of sound in air is 335m/s, the number of beats heard per second by the driver is
View Solutiona bus is moving towards and stationary observer with speed 20 m/s blows a horn of frequency 200 Hz. the frequency of sound heard by the observer is approximately ( take speed of sound 320 m/s)
View SolutionA car is moving towards a fixed wall, it blows form of frequency of 440Hz . The frequency of reflected sound observed by the driver is 480Hz then find the speed of car in km/hr. (Speed of sound is 350msec
View Solution

