A charge Q is fixed on the X-Y plane at point (0, a). Find the electric field strength component along the X-axis, at any point (x, 0).
The correct Answer is:14π∈0Qx(a2+x2)3/2
To find the electric field strength component along the X-axis at a point (x, 0) due to a charge Q fixed at the point (0, a), we can follow these steps:
Step 1: Identify the position of the charge and the point of interest
The charge Q is located at the point (0, a) on the XY-plane, and we need to find the electric field at the point (x, 0) on the X-axis.
Step 2: Calculate the distance between the charge and the point
The distance r between the charge at (0, a) and the point (x, 0) can be calculated using the distance formula:
r=√(x−0)2+(0−a)2=√x2+a2
Step 3: Write the expression for the electric field
The electric field E due to a point charge is given by the formula:
E=kQr2
where k is Coulomb's constant.
Step 4: Substitute the distance into the electric field formula
Substituting r into the electric field formula gives:
E=kQ(√x2+a2)2=kQx2+a2
Step 5: Determine the components of the electric field
Since we are interested in the component of the electric field along the X-axis, we need to consider the direction of the electric field vector. The electric field vector points away from the charge if the charge is positive and towards the charge if it is negative.
The electric field vector →E can be resolved into components. The X-component Ex can be found using:
Ex=E⋅x√x2+a2
Substituting E from the previous step:
Ex=kQx2+a2⋅x√x2+a2=kQx(x2+a2)3/2
Final Result
Thus, the electric field strength component along the X-axis at the point (x, 0) is:
Ex=kQx(x2+a2)3/2
The charge Q is located at the point (0, a) on the XY-plane, and we need to find the electric field at the point (x, 0) on the X-axis.
The distance r between the charge at (0, a) and the point (x, 0) can be calculated using the distance formula:
r=√(x−0)2+(0−a)2=√x2+a2
The electric field E due to a point charge is given by the formula:
E=kQr2
where k is Coulomb's constant.
Substituting r into the electric field formula gives:
E=kQ(√x2+a2)2=kQx2+a2
Since we are interested in the component of the electric field along the X-axis, we need to consider the direction of the electric field vector. The electric field vector points away from the charge if the charge is positive and towards the charge if it is negative.
Ex=E⋅x√x2+a2
Substituting E from the previous step:
Ex=kQx2+a2⋅x√x2+a2=kQx(x2+a2)3/2
Thus, the electric field strength component along the X-axis at the point (x, 0) is:
Ex=kQx(x2+a2)3/2
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-I)13videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Exercise57videos
ELECTRIC CHARGES AND FIELDS
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Additional Exercise11videos
ELECTROMAGNETIC INDUCTION
Similar Questions
A point charge q is located at the centre fo a thin ring of radius R with uniformly distributed charge −q, find the magnitude of the electric field strength vectro at the point lying on the axis of the ring at a distance x from its centre, if x>>R.
View SolutionA ring of radius a contains a charge q distributed. uniformly ober its length. Find the electric field at a point. on the axis of the ring at a distance x from the centre.
View SolutionThree point charges q,−2q and q are located along the x-axis a s shown in figure. Show that the electric field at P(y>>a) along the y-axis is,
E=−14πε03qa2y4ˆj
 View Solution
View SolutionA point charge q=−8.0nC is located at the origin. Find the electric field vector at the point x=1.2m,y=−1.6m.
View SolutionIn a certain region of space, there exists a uniform and constant electric field of strength E along x-axis and uniform constant magnetic field of induction B along z-axis. A charge particle having charge q and mass m is projected with speed v parallel to x-axis from a point (a, b, 0). When the particle reaches a point( 2a, b/2, 0) its speed becomes 2v. Find the value of electric field strength in term of m, v and co-ordinates.
View SolutionIn figure two positive charges q2 and q3 fixed along the y-axis ,exert a net electric force in the +x direction on a charge q1 fixed along the x-axis if a positive charge Q is added at (x,0) the force on q1
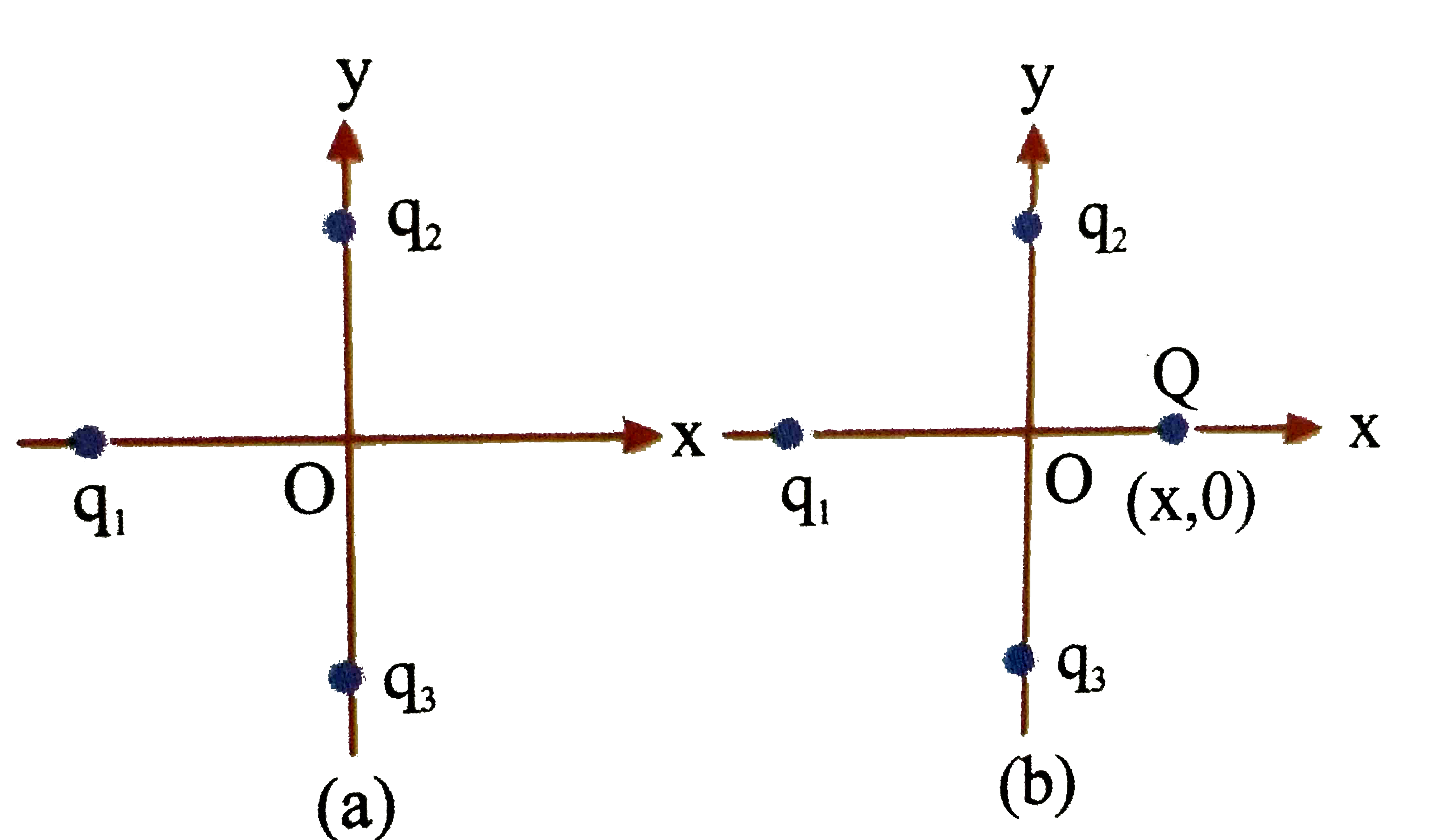 View Solution
View SolutionIn figure two positive charges q2 and q3 fixed along the y-axis ,exert a net electric force in the +x direction on a charge q1 fixed along the x-axis if a positive charge Q is added at (x,0) the force on q1
 View Solution
View SolutionA uniform surface charge of density σ is given to a quarter of a disc extending up to infinity in the first quadrant of x−y plane. The centre of the disc is at the origin O. Find the z-component of the electric field at the point (0,0,z) and the potential difference between the point (0,0,d) and (0,0,2d)
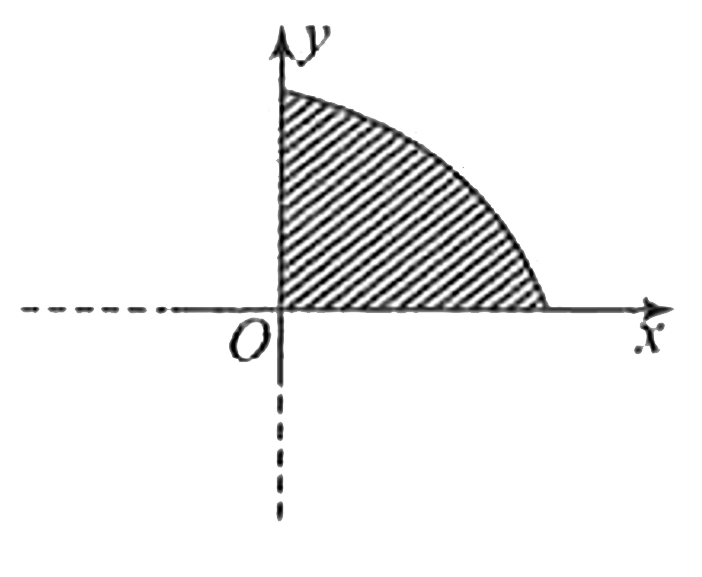 View Solution
View SolutionTwo charges q1 and q2 are kept on x-axis and electric field at different points an x-axis is plotted against x. Choose correct statement about nature and magnitudes of q1 and q2
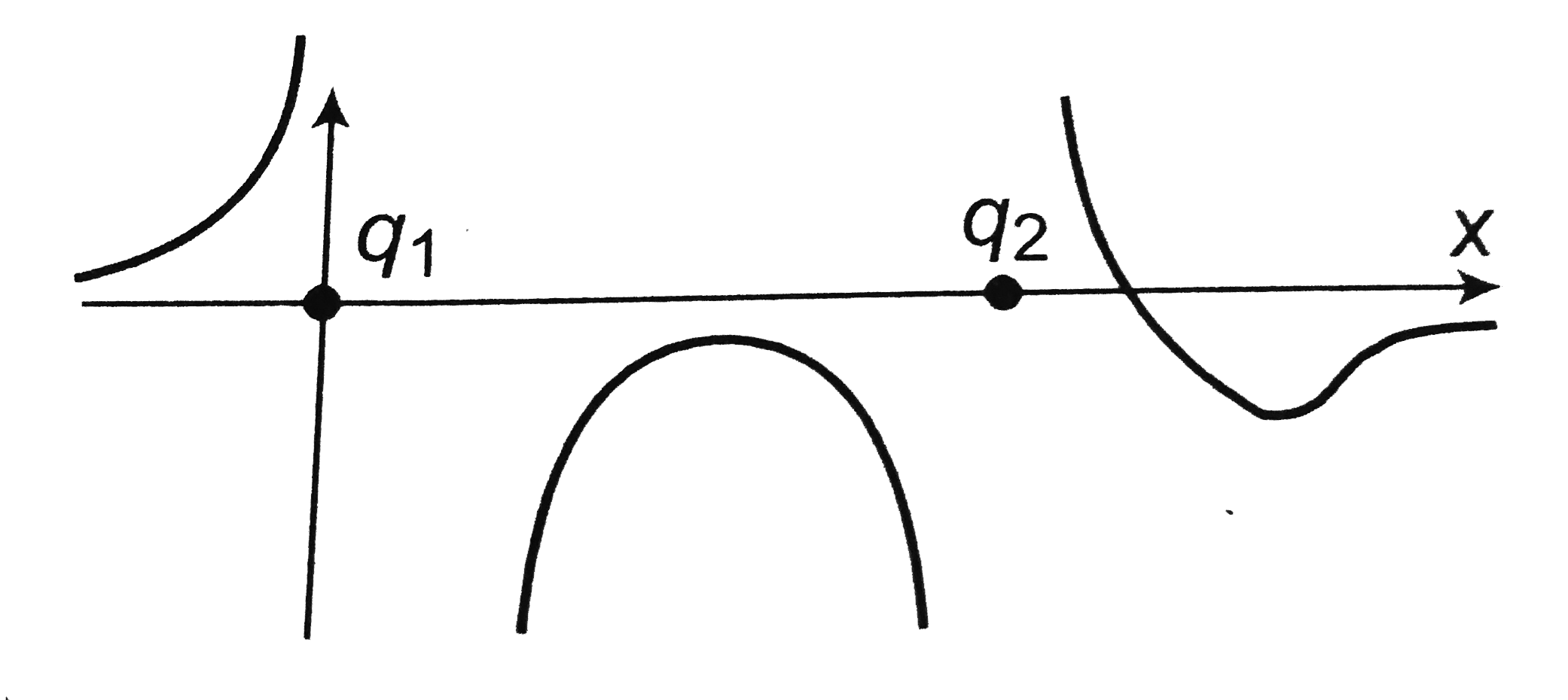 View Solution
View SolutionAn electric dipole is placed at the origin O and is directed along the x-axis. At a point P, far away from the dipole, the electric field is parallel to y-axis. OP makes an angle θ with the x-axis then
View Solution
