A charged particle P has a mass of 10−16kg and carries a charge of 4.9×10−19C. Calculate the intensity of the electric field to be applied on it in vertically upward direction, so as to keep it at rest.
The correct Answer is:2×103N/C
To solve the problem of finding the intensity of the electric field required to keep a charged particle at rest, we can follow these steps:
Step 1: Identify the Forces Acting on the Particle
The charged particle experiences two main forces:
1. The gravitational force acting downward, which is given by Fg=mg.
2. The electric force acting upward due to the electric field, which is given by Fe=QE.
Step 2: Set Up the Equation for Equilibrium
For the particle to remain at rest, the upward electric force must balance the downward gravitational force. Therefore, we can set up the equation:
QE=mg
Step 3: Rearrange the Equation to Solve for Electric Field E
We can rearrange the equation to solve for the electric field E:
E=mgQ
Step 4: Substitute the Given Values
Now, we substitute the given values into the equation:
- Mass m=10−16 kg
- Charge Q=4.9×10−19 C
- Acceleration due to gravity g=10m/s2
Substituting these values into the equation gives:
E=(10−16kg)(10m/s2)4.9×10−19C
Step 5: Calculate the Electric Field E
Now, we perform the calculation:
E=10−154.9×10−19=10−154.9×1019
E≈2.04×103N/C
Final Answer
The intensity of the electric field required to keep the charged particle at rest is approximately:
E≈2.04×103N/C
---
The charged particle experiences two main forces:
1. The gravitational force acting downward, which is given by Fg=mg.
2. The electric force acting upward due to the electric field, which is given by Fe=QE.
For the particle to remain at rest, the upward electric force must balance the downward gravitational force. Therefore, we can set up the equation:
QE=mg
We can rearrange the equation to solve for the electric field E:
E=mgQ
Now, we substitute the given values into the equation:
- Mass m=10−16 kg
- Charge Q=4.9×10−19 C
- Acceleration due to gravity g=10m/s2
E=(10−16kg)(10m/s2)4.9×10−19C
Now, we perform the calculation:
E=10−154.9×10−19=10−154.9×1019
E≈2.04×103N/C
The intensity of the electric field required to keep the charged particle at rest is approximately:
E≈2.04×103N/C
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)26videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - EXERCISE (VERY SHORT ANSWER QUESTIONS)23videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Exercise57videos
ELECTRIC CHARGES AND FIELDS
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Additional Exercise11videos
ELECTROMAGNETIC INDUCTION
Similar Questions
A charged particle having a mass of 1.6×10−26kg comes out of accelerator tube with kinetic energy 2×103eV . Calculate the smallest magnitude of the magnetic field that should be applied in vertically downwards direction to just prevent the charged particle from colliding the plate (Assume charge on particle = charge of the proton)
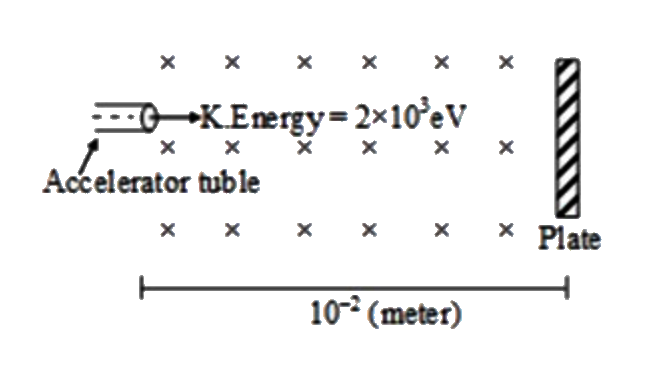 View Solution
View SolutionTwo positively charged particles each of mass is 9×10−30kg and carrying a charge of 1.6×10−19C are placed at a distance .r. apart. If each experiences a force equal to its weight, the value of r is (g=10ms−2)
View Solution
Knowledge Check
- Question 1 - Select One
A force of 2.25 N acts on a charge of 15×10−4C. The intensity of electric field at that point is
A150NC−1B15NC−1C1500NC−1D1.5NC−1 - Question 2 - Select One
A body has a positive charge of 8×10−19C. It has :
Aan excess of 5 electronsBa deficiency of 5 electronsCan excess of 8 electronsDa deficiency of 8 electrons
Two positively charged small particles, each of mass 1.7×10−27kg and carrying a charge of 1.6×10−19C are placed apart at a separation r. If each one experiences a repulsive force equal to its weight find their separation.
View SolutionTwo positively charged small particles, each of mass 1.7×10−27kg and carrying a charge of 1.6×10−19C are placed apart at a separation r. If each one experiences a repulsive force equal to its weight find their separation.
View SolutionA water particle of mass 10.0 mg and having a charge of 1.50×10−6C stays suspended in a room. What is the magnitude of electric field in the room ? What is its direction?
View SolutionA drop of 10−6 kg water carries 10−6C charge. What electric field should be applied to balance its weight (assume g=10ms−2)
View SolutionA particle having a mass of 0.5g carries a charge of 2.5×10−8C. The particle is given an initial horizontal velocity of 6×104ms−1. To keep the particle moving in a horizontal direction
View SolutionA pendulum bob of mass 80mg and carrying a charge of 2×10−8C is at rest in a uniform, horizontal electric field of 20k Vm−1. Find the tension in the thread.
View Solution
