A container A is having some fluid of density θ0. If is connected with a U tube manometer shown in figure. Find the pressure of the container in both the cases given in figure.
To solve the problem of finding the pressure in the container A connected to a U-tube manometer, we will analyze both cases as described in the video transcript.
2. Pressure at point C:
- The pressure at point C can be expressed as:
PC=ρg(h1+h2)
where ρ is the density of the manometer fluid and h2 is the height of the fluid column above point C.
3. Equate pressures at points B and C:
- Since points B and C are at the same level, we can set their pressures equal:
PA+ρ0gh1=ρg(h1+h2)
4. Rearranging the equation:
- Rearranging gives:
PA=ρg(h1+h2)−ρ0gh1
- Simplifying further:
PA=ρgh2+(ρ−ρ0)gh1
5. Absolute Pressure:
- If P0 is the atmospheric pressure, the absolute pressure at point A is:
P′A=PA+P0=ρgh2+(ρ−ρ0)gh1+P0
Case 2:
1. Identify the pressures at points B and C:
- Again, let the pressure at point A be PA.
- The pressure at point B can be expressed as:
PB=PA+ρ0gh1
2. Pressure at point C:
- The pressure at point C can be expressed as:
PC=ρg(h2−h1)
3. Equate pressures at points B and C:
- Setting the pressures equal gives:
PA+ρ0gh1=ρg(h2−h1)
4. Rearranging the equation:
- Rearranging gives:
PA=ρg(h2−h1)−ρ0gh1
- Simplifying further:
PA=ρgh2−(ρ+ρ0)gh1
5. Absolute Pressure:
- The absolute pressure at point A is:
P′A=PA+P0=ρgh2−(ρ+ρ0)gh1+P0
Final Results:
- Case 1:
PA=ρgh2+(ρ−ρ0)gh1
P′A=ρgh2+(ρ−ρ0)gh1+P0
- Case 2:
PA=ρgh2−(ρ+ρ0)gh1
P′A=ρgh2−(ρ+ρ0)gh1+P0
- The pressure at point C can be expressed as:
PC=ρg(h1+h2)
where ρ is the density of the manometer fluid and h2 is the height of the fluid column above point C.
- Since points B and C are at the same level, we can set their pressures equal:
PA+ρ0gh1=ρg(h1+h2)
- Rearranging gives:
PA=ρg(h1+h2)−ρ0gh1
- Simplifying further:
PA=ρgh2+(ρ−ρ0)gh1
- If P0 is the atmospheric pressure, the absolute pressure at point A is:
P′A=PA+P0=ρgh2+(ρ−ρ0)gh1+P0
1. Identify the pressures at points B and C:
- Again, let the pressure at point A be PA.
- The pressure at point B can be expressed as:
PB=PA+ρ0gh1
- The pressure at point C can be expressed as:
PC=ρg(h2−h1)
- Setting the pressures equal gives:
PA+ρ0gh1=ρg(h2−h1)
- Rearranging gives:
PA=ρg(h2−h1)−ρ0gh1
- Simplifying further:
PA=ρgh2−(ρ+ρ0)gh1
- The absolute pressure at point A is:
P′A=PA+P0=ρgh2−(ρ+ρ0)gh1+P0
- Case 1:
PA=ρgh2+(ρ−ρ0)gh1
P′A=ρgh2+(ρ−ρ0)gh1+P0
PA=ρgh2−(ρ+ρ0)gh1
P′A=ρgh2−(ρ+ρ0)gh1+P0
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples
7 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.1
11 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A liquid of density 'ρ' is rotated with an angular speed 'ω' as shown in figure. Using the pressure equation concept find the equation of free surface of the liquid.
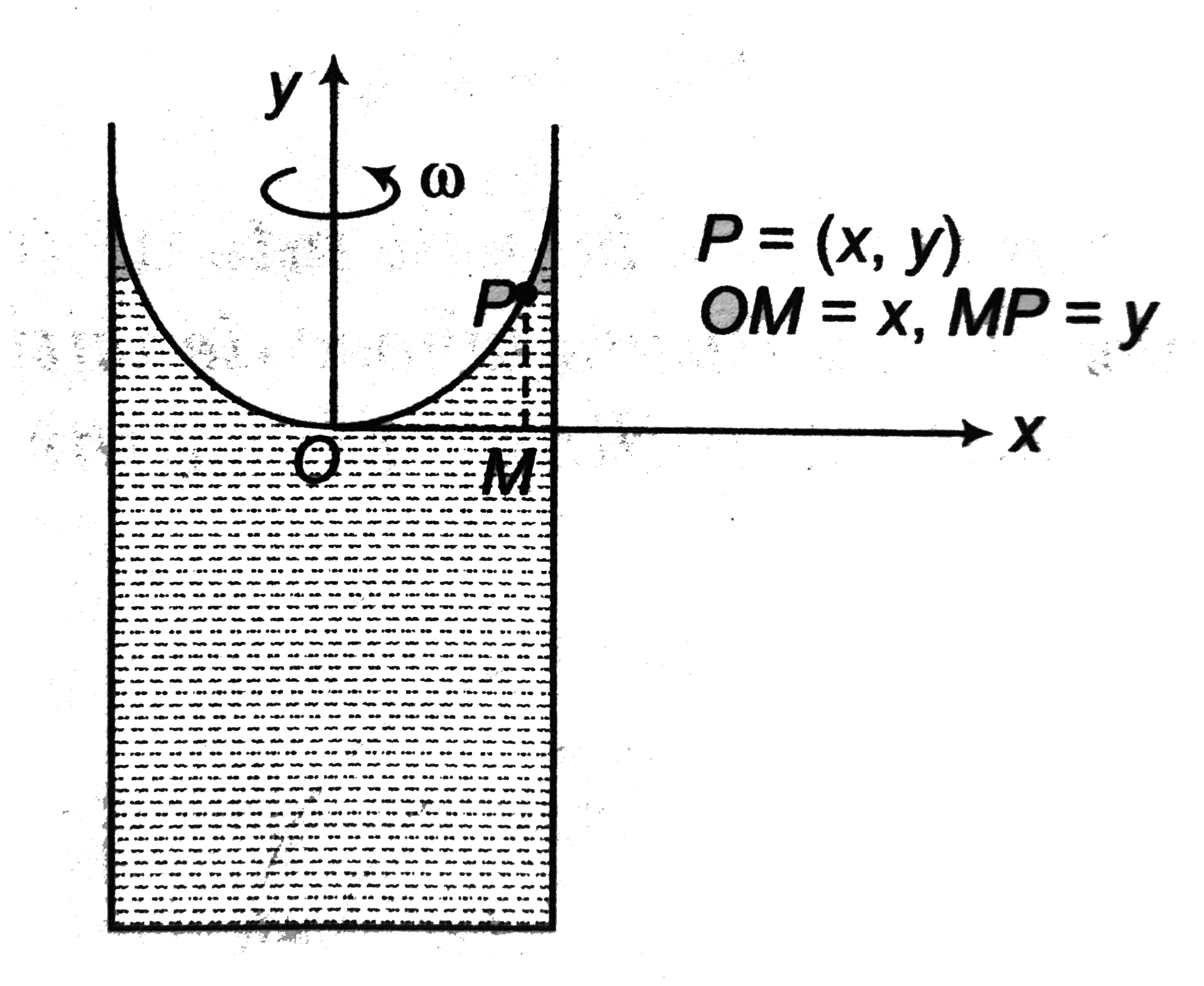 .
.
View Solution
A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
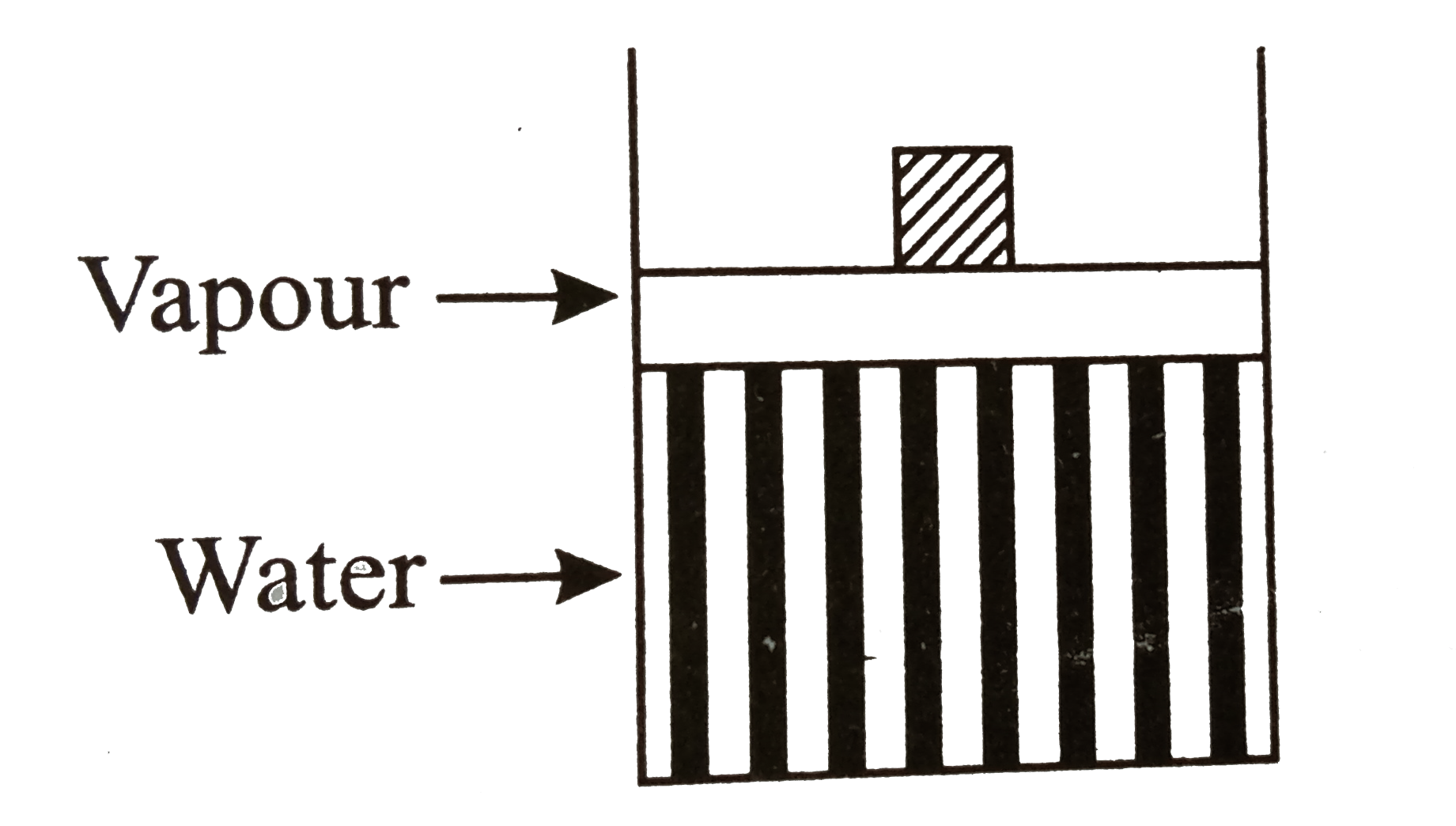
View SolutionSome quantity of water is contained in a container as shown in figure. As neon is added to this system at constant pressure, the amount of liquid water in the vessel
View SolutionA liquid kept in a container has a horizontal acceleration 'a' as shown in figure.
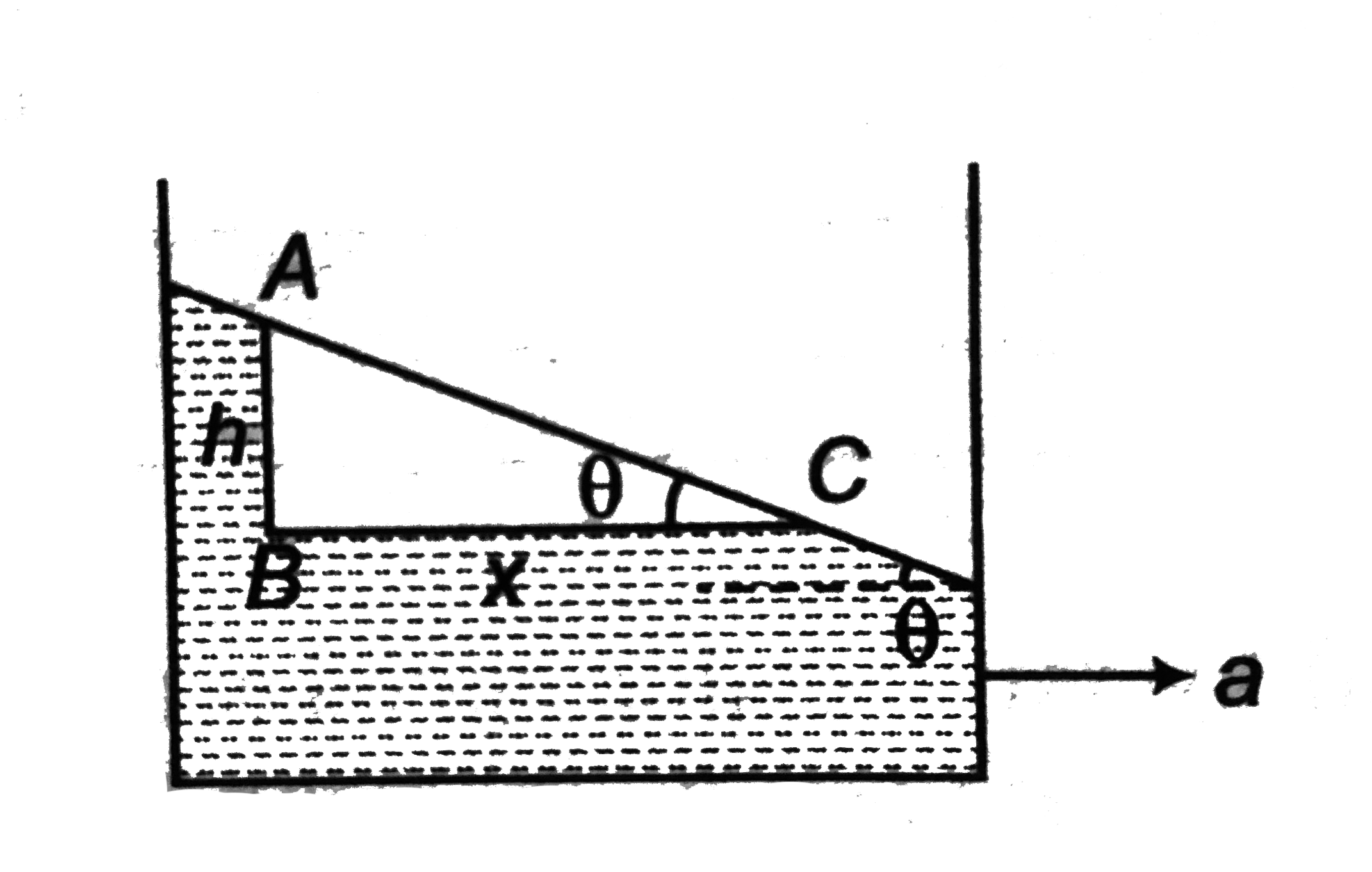
Using the pressure equation along the path ABC find the angle θ.
View SolutionFind out pressures at point A and B. Also find angle θ. A zig zag tube open at n, having liquis of densities ρ1,ρ2 and ρ3 is placed in a vertical plane as shown in figure. (The pressue at M is equal to atmospheric pressure).

View SolutionA sealed tank containing a liquid of density ρ moves with horizontal acceleration a as shown in the figure. The difference in pressure between two points A and B will be

View SolutionFigure shows as thin tube open at one end rotating with constant angular speed ω. The other end of the tube has a small opening. Tube contains a fluid of density ρ which effuses with speed u relative to the tube. Let ρA be the pressure at the point in the tube just behind the opening. Assume the atmospheric pressure to be p0 and pick correct option(s) for the instant when h=l2

View SolutionA circuit containing five resistors is connected to a battery with a 12 v emf as shown in figure. The potential difference across 4Ω resistor is

View SolutionIn a U-tube, two immiscible liquids of density ρ1andρ2 are arranged as shown in figure. The right part of the tube is closed at the top and some air is entrapped above liquid of density ρ2. The gauge pressure of this air is :

View SolutionA siphon tube is discharging a liquid of specific gravity 0.9 from a reservoir as shown in the figure.

(a) Find the velocity of the liquid through the siphon.
(b) Find the pressure at the highest point B.
(c ) Find the pressure at point C.
View Solution
