A convex spherical refracting surfaces separates two media glass and air (μg=1.5). If the image is to be real, at what minimum distance u should the object be placed in air if R is the radius of curvature
u>3R
u>2R
u>4R
u>R
The correct Answer is:B
To solve the problem step-by-step, we will use the refraction formula for a curved surface and analyze the conditions for a real image.
1. Understand the Setup:
- We have a convex spherical refracting surface separating two media: glass (with refractive index μg=1.5) and air (with refractive index μa=1.0).
- The object is placed in air, and we need to find the minimum distance u from the surface where the object should be placed to ensure that the image formed is real.
2. Sign Convention:
- According to the sign convention, the radius of curvature R for a convex surface is taken as positive.
- The object distance u is negative since the object is placed on the side from which light is coming (left side of the surface).
3. Refraction Formula:
- The formula for refraction at a curved surface is given by:
μ2v−μ1u=μ2−μ1R
- Here, μ2=1.5 (glass), μ1=1.0 (air), and R is positive.
4. Substituting Values:
- Substitute the values into the formula:
1.5v−1.0−u=1.5−1.0R
- This simplifies to:
1.5v+1.0u=0.5R
5. Rearranging the Equation:
- Rearranging gives:
1.5v=0.5R−1.0u
- This can be rewritten as:
1.5v=12R−1u
6. Condition for Real Image:
- For the image to be real, v must be positive. Therefore, we require:
12R>1u
- This implies:
u>2R
7. Conclusion:
- The minimum distance u at which the object should be placed in air for the image to be real is:
u>2R
Final Answer:
The object should be placed at a distance u greater than 2R from the refracting surface.
---
- We have a convex spherical refracting surface separating two media: glass (with refractive index μg=1.5) and air (with refractive index μa=1.0).
- The object is placed in air, and we need to find the minimum distance u from the surface where the object should be placed to ensure that the image formed is real.
- According to the sign convention, the radius of curvature R for a convex surface is taken as positive.
- The object distance u is negative since the object is placed on the side from which light is coming (left side of the surface).
- The formula for refraction at a curved surface is given by:
μ2v−μ1u=μ2−μ1R
- Here, μ2=1.5 (glass), μ1=1.0 (air), and R is positive.
- Substitute the values into the formula:
1.5v−1.0−u=1.5−1.0R
- This simplifies to:
1.5v+1.0u=0.5R
- Rearranging gives:
1.5v=0.5R−1.0u
- This can be rewritten as:
1.5v=12R−1u
- For the image to be real, v must be positive. Therefore, we require:
12R>1u
- This implies:
u>2R
- The minimum distance u at which the object should be placed in air for the image to be real is:
u>2R
The object should be placed at a distance u greater than 2R from the refracting surface.
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Single Correct Option
3 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - more than one correct option
1 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Subjective Questions
8 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
Trace the rays of light showing the formation of an image due to a point object placed on the axis of a spherical surface separating the two media of refractive indices n1andn2. Establish the relation between the distance of the object, the image and the radius of curvature from the central point of the spherical surface.
Hence derive the expression of the lens maker's formula
View SolutionRefraction takes place at a convex spherical boundary separating air-glass medium. For the image to be real, the object distance (μg=3/2)
Note Object lying in the glass.
View Solution(a) A point object, O is on the principle axis of a spherical surface having a radius of curvature, R. Draw a diagram to obtain the relation between the object and image distances, the refractive indicess of the media and the radius of curvature of the spherical surface.
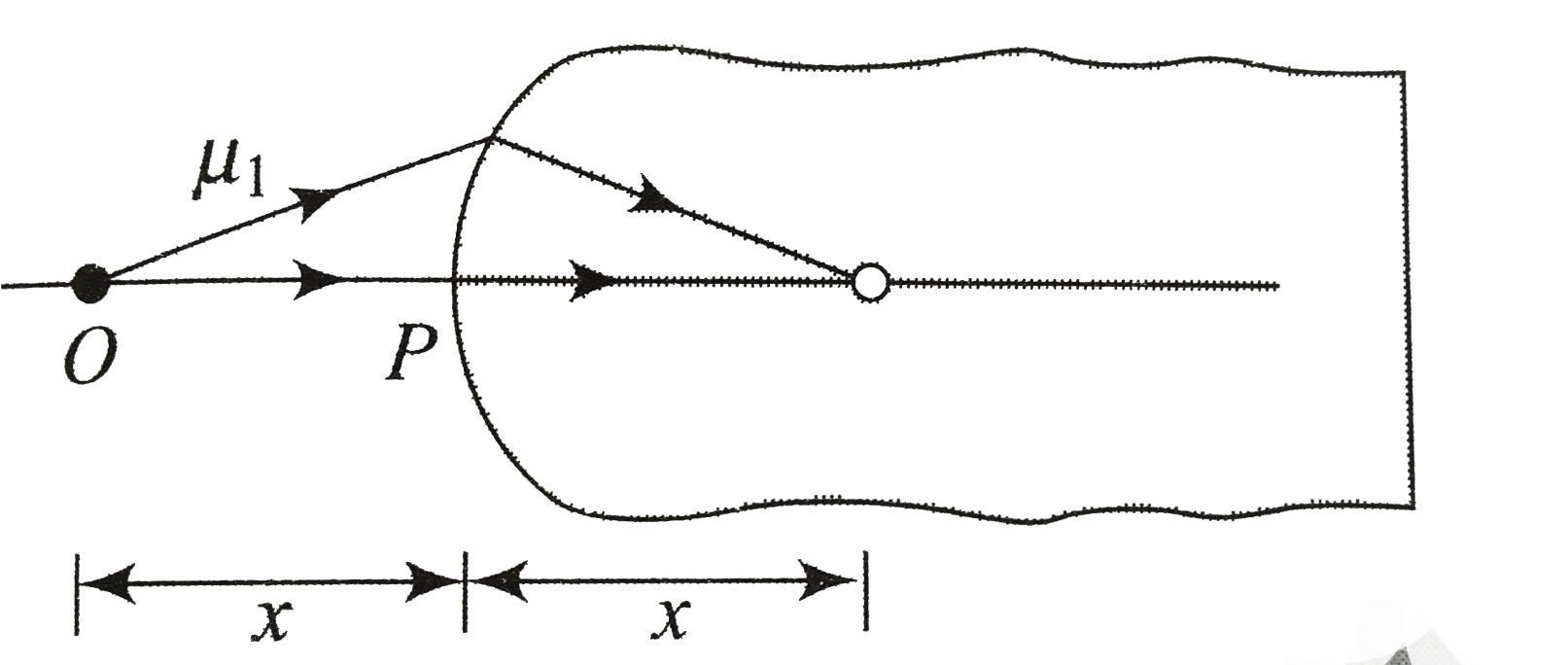
View SolutionA spherical surface of radius R ssparates two media of refractive indices μ1 and μ1 as shown in figure., Where should an object be placed in medium 1 so that a real image is formed in medium 2 at the same distance?
View SolutionThe minimum sum of the distances of a real object and a real image from a concave mirror of radius of curvature 20cm is:
View SolutionWhat can be the largest distance of an image of real object from a convex mirror of radius of curvature is 20cm ?
View SolutionShow that for refraction at a concave spherical surface (separating glass-air medium), the distance of the object should be greater than three times the radius of curvature of the refracting surface for the image to be real.
View SolutionRadius of curvature of a concave spherical surface separating air-glass medium is R. A point object is placed on the principal axis in the glass (mg=1.5). For the image to be real seen by

observer in air, distance of the object from P should be
View SolutionA spherical surface of radius of curvature R separates air (refractive index 1.0) from glass (refractive index 1.5). The center of curvature is in the glass. A point object P placed in air is found to have a real image Q in the glass. The ling PQ cuts the surface at a point O, and PO=OQ. The distance PO is equal to
View SolutionA concave spherical surface of radius of curvature 100 cm separates two media of refractive indices 1.50 and 43. An object is kept in the first medium at a distance of 30 cm from the surface. Calculate the position of the image.
View Solution
