A crane has an arm length of 20 m inclined at 30° with the vertical. It carries a container of mass of 2 ton suspended from the top end of the arm. Find the torque produced by the gravitational force on the container about the point where the arm is fixed to the crane. [Given: 1 ton = 1000 kg, neglect the weight of the arm. g−10ms−2]
Solution in Tamil
The force at the point of suspension is due to the weight of the hanging mass
F=mg=2×100×10=20000N
The are length r=20 m
We can solve this problem by three different methods.
Method-1: The angle () between the arm length() and the force (F) is θ=150∘ The torque (t) about the fixed point of the arm is,
τ=rFsinθ
τ=20×2000×sin(150∘)
=400000×sin(90∘+60∘) [heresin(90∘+θ)=cosθ]
=400000×12[cos60∘=12]=200000Nm
τ=2×105Nm
Method-II: Let us take the force and perpendicular distance from the point where the arm is fixed to the crane
τ=(r⊥)F
τ=rcosϕimg
τ=20×cos60×20000
=20×12×20000=200000Nm
τ=2×104Nm

Method-III: Let us take the distance from the fixed point and perpendicular force
τ=(F⊥)
τ=rmgcosϕ
ta=20×20000×cos60∘
=20×20000×12)=200000Nm,
τ=2x105Nm
All the three methods, give the same answer

Topper's Solved these Questions
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODIESBOOK - FULL MARKSCHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODIESEXERCISE - TEXTUAL QUESTIONS SOLVED ( MULTIPLE CHOICE QUESTIONS:)
15 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODIESBOOK - FULL MARKSCHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODIESEXERCISE - TEXTUAL QUESTIONS SOLVED ( SHORT ANSWER QUESTIOS)
17 Videos
- LAW OF MOTION BOOK - FULL MARKSCHAPTER - LAW OF MOTION EXERCISE - ADDITIONAL QUESTIONS SOLVED (SHORT ANSWER QUESTIONS (3 MARKS & NUMERICALS))
16 Videos
- NATURE OF PHYSICAL WORLD AND MEASUREMENT BOOK - FULL MARKSCHAPTER - NATURE OF PHYSICAL WORLD AND MEASUREMENT EXERCISE - ADDITIONAL QUESTIONS SOLVED ( SHORT ANSWER QUESTIONS (2 MARK))
20 Videos
Similar Questions
The centre of mass of a system of particles does not depend upon
View SolutionDefine the center of mass of a body.
View SolutionA block of mass 500 g is at rest on a horizontal table. What steady force is required to give the block a velocity of 200cms−1 in 4 s?
View SolutionThe vernier scale of a travelling microscope has 50 divisions which coincide with 49 main scale divisions. If each main scale division is 0.5 mm. Calculate the minimum inaccuracy in the measurement of distance.
View SolutionLength of horizontal arm of a uniform cross section U -tube is l= 21 cm and ends of both of the vertical arms are open to surrounding of pressure 10500 N//m^(2) . A liquid of density rho = 10^(3) kg//m^(3) is poured into the tube such that liquid just fills the horizontal part of the tube. Now one of the open ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm With angular velocity omega_(0) = 10 rad//s . If length of each vertical arm is a = 6 cm , calculate the length of air column in the sealed arm. (in cm)
View SolutionThe inner diameter of a cylinderical wooden pipe is 24 cm and its outer diameter is 28 cm. The length of the pipe is 35 cm. Find the mass of the pipe, if 1cm3 of wood has a mass of 0.6 g.
View Solutionकिसी त्रिभुज की भुजाऐं 30 मी., 72 मी, तथा 78 मी., हैं। 72 मीटर भुजा पर डाले गये शीर्षलम्ब की लम्बाई ज्ञात करें?
View SolutionA crane lifts a mass of 100 kg to a height of 10 m in 20 s. The power of the crane is (Take g = 10 m s^(-2) )
View Solutionएक ट्रक विरामवस्था से किसी पहाड़ी से नीचे की ओर नियत त्वरण से लुढ़कना शुरू करता है | यह 20 s में 400 m की दुरी तय करता है | इसका त्वरण ज्ञात करें | अगर इसका द्रव्यमान 7 टन है तो उस पर लगने वाले बल की गणना करें | (1टन = 1000 kg )
View Solutionएक वर्ग की भुजा ज्ञात कीजिय , जिसका परिमाप 20 मी है ।
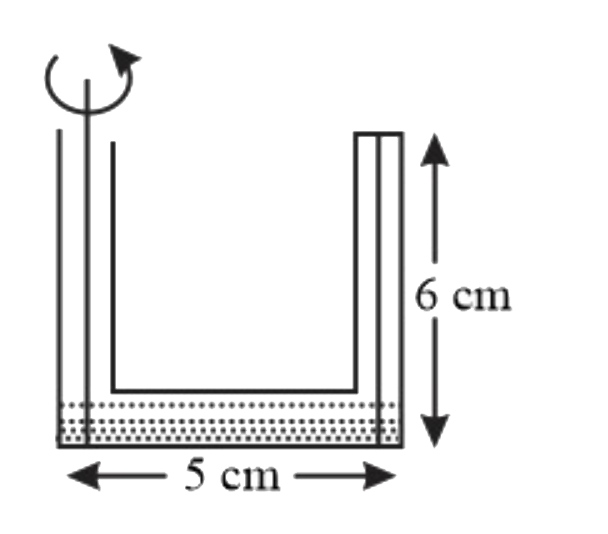
View SolutionLength of the horizontal arm of a uniform cross - section U - tube is l = 5 cm and both ends of the vertical arms are open to the surrounding pressure of 7700 N m−2. A liquid of density ρ=103 kg m−3 is poured into the tube such that the liquid just fills the horizontal part of the tube. Now, one of the open ends is sealed and the tube. Now, one of the open ends is sealed and the tube is then rotaed about a vertical axis passing through the other veritcal arm with angular velocity ω due to which the liquid rises up to half the length of the vertical arm. If length of each vertical arm is a = 6 cm. What is the value of ω(in rad s−1)?
View Solutionএকটি ত্রিভুজের বৃহত্তম বাহু ক্ষুদ্রতম বাহুর তিনগুণ এবং তৃতীয় বাহুটি বৃহত্তম বাহুর দৈঘ্য অপেক্ষা 2 সেমি ছোটো।ত্রিভুজটির পরিসীমা কম করে 61 সেমি হলে ক্ষুদ্রতম বাহুর অবম মান হবে-
View SolutionA road is 8 m chi 40 m. Find the upward velocity of the arm on the road. (g = 10 m//s^(2))
View SolutionA crane lifts a mass of 100 kg to a height of 10 m in 20 s. The power of the crane is (Take g = 10 m s^(-2) )
View SolutionThe angular frecuancy needed for a centrifugal to produce an acceleration of 1000 g rad/s^(2) at a radius arm of 10 cm ,is
View Solution
