A cylinder rotating at an angular speed of 50 rev/s is brought in contact with an identical stationary cylinder. Because of the kinetic friction, torques act on the two cylinders, accelerating the stationary one and decelerating the moving one. If the common magnitude of the acceleration and deceleration be one revolution per second square, how long will it take before the two cylinders have equal angular speed?
The correct Answer is:B
To solve the problem, we need to analyze the motion of both cylinders and determine the time it takes for them to reach the same angular speed.
1. Identify Initial Conditions:
- For Cylinder 1 (the rotating cylinder):
- Initial angular speed, ω01=50rev/s
- Angular acceleration, α1=−1rev/s2 (deceleration due to friction)
- For Cylinder 2 (the stationary cylinder):
- Initial angular speed, ω02=0rev/s
- Angular acceleration, α2=+1rev/s2 (acceleration due to friction)
2. Use the Angular Motion Equation:
The angular motion equation is given by:
ω=ω0+αt
We will apply this equation to both cylinders.
3. Apply the Equation for Cylinder 1:
For Cylinder 1:
ω=50+(−1)t
Simplifying, we have:
ω=50−t(1)
4. Apply the Equation for Cylinder 2:
For Cylinder 2:
ω=0+(1)t
Simplifying, we have:
ω=t(2)
5. Set the Angular Velocities Equal:
Since both cylinders will have the same final angular speed ω at time t, we can set equations (1) and (2) equal to each other:
50−t=t
6. Solve for Time t:
Rearranging the equation:
50=2t
Dividing both sides by 2:
t=25seconds
Final Answer:
The time it takes for the two cylinders to have equal angular speed is t=25seconds.
- For Cylinder 1 (the rotating cylinder):
- Initial angular speed, ω01=50rev/s
- Angular acceleration, α1=−1rev/s2 (deceleration due to friction)
- For Cylinder 2 (the stationary cylinder):
- Initial angular speed, ω02=0rev/s
- Angular acceleration, α2=+1rev/s2 (acceleration due to friction)
The angular motion equation is given by:
ω=ω0+αt
We will apply this equation to both cylinders.
For Cylinder 1:
ω=50+(−1)t
Simplifying, we have:
ω=50−t(1)
For Cylinder 2:
ω=0+(1)t
Simplifying, we have:
ω=t(2)
Since both cylinders will have the same final angular speed ω at time t, we can set equations (1) and (2) equal to each other:
50−t=t
Rearranging the equation:
50=2t
Dividing both sides by 2:
t=25seconds
The time it takes for the two cylinders to have equal angular speed is t=25seconds.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer21videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -214videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer13videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer15videos
SIMPLE HARMONIC MOTION
Similar Questions
Two thin planks are moving on a four identical cylinders as shown. There is no slipping at any contact points. Calculate the ratio of angular speed of upper cylinder to lower cylinder
 View Solution
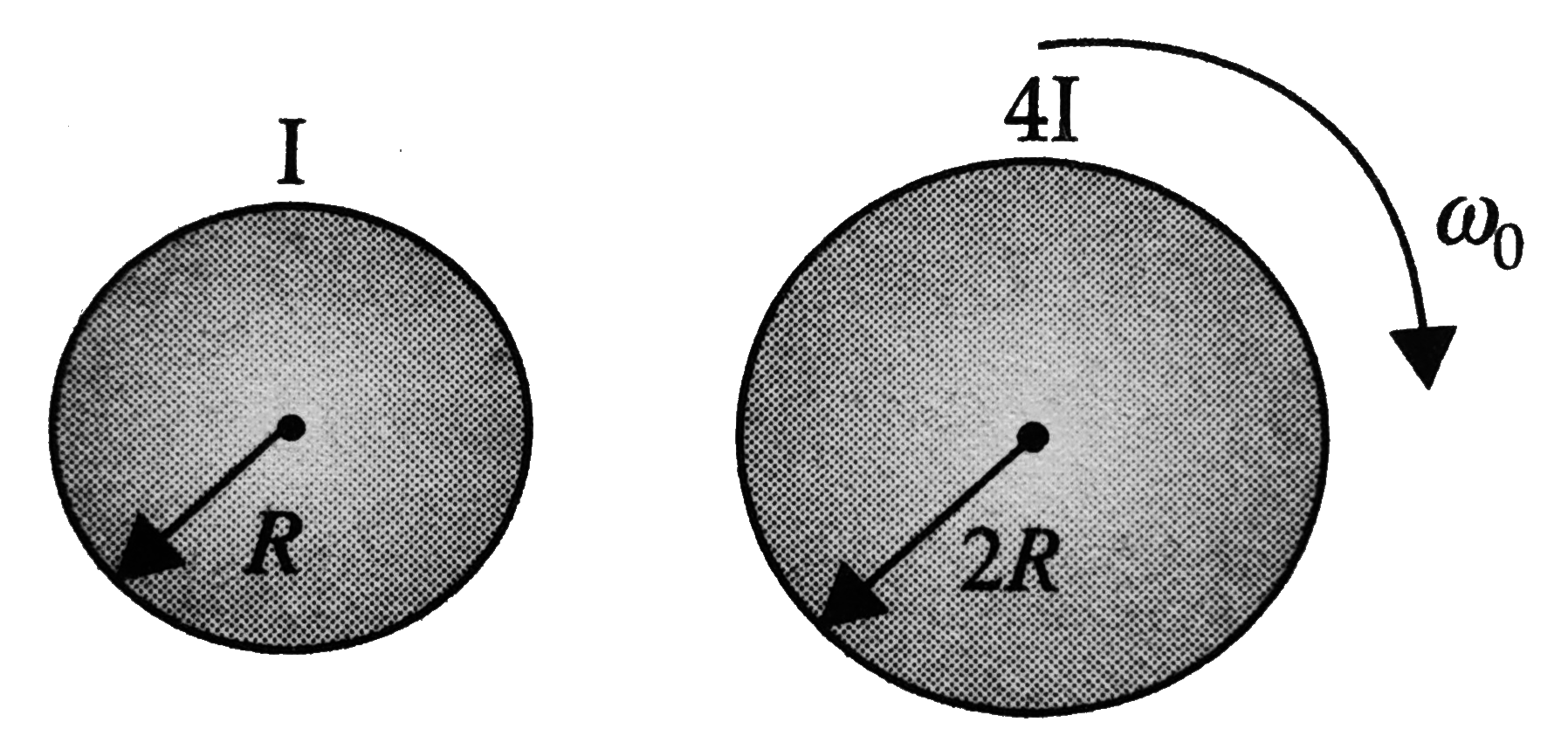
View SolutionTwo cylinders having radii 2R and R and moment of inertia 4I and I about their central axes are supported by axles perpendicular to their planes. The large cylinder is initially rotating clockwise with angular velocity ω0. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually slipping ceases and the two cylinders rotate at constant rates in opposite directions. During this
(A) angular momentum of system is conserved
(B) kinetic energy is conserved
(C neither the angular momentum nor the kinetic energy is conserved
(D) both the angular momentum and kinetic energy are conserved
 View Solution
View SolutionAn amusement park ride consist of a large verticle cylinder that spins about its axis first fast enough that any person inside is held up againest the wall when the is μs and the radius of the cylider is R

a. Shown that maximum period of revolation neccessary to keep the person from falling is T=(4π2μsR/g)1/2
b. Obtain a numerical value for T taking R=4.00m and μs=0.400 . How many revolations per minute does the cylinder make?
c. If the rate of revolation of the cylinder is make to be some what larger what happens to the magnitude of each one of the forces acting on the person ? What happens to the motion of the person ?
d. If instead the cylinder rate revolution is made to be somewhat smaller what happens to the magnitude and what happens to the motion of the person ?View SolutionFigure shows two cylinders of radii r1andr2 having moments of inertia I1andI2 about their respective axes. Initially the cylinders rotate about their axes with angular speed ω1andω2 as shown in the figure. The cylinders are moved closer to touch each other keeping the axes parallel. The cylinders first slip over each other at the contact but the slipping finally ceases due to the friction between them. Find the angular speeds of the cylinders after the slipping ceases.
 View Solution
View SolutionA solid cylinder of mass 50kg and radius 0.5m is free to rotate about the horizontal axis. A massless string is wound round the cylinder with one end attached to it and other end hanging freely. Tension in the string required to produce an angular acceleration of 2 revolution s−2 is
View SolutionCarbon monoxide emitted by automobiles is an environmental hazard . A car has an engine of four cylinders with a total cylinder volume of 1600 cc and a fuel consumption fo 7.0 dm3 per 100 Km , when driving at an average speed of 80 km/hr . In one second , each cylinder goes through 25 burn cycles and consumes 0.400g of fuel . The compression ratio, which is the ratio between the smallest and largest volume within the cylinder as the piston moves forward and backward is 1:8.
Calculate the air intake of the engine (m3S−1) , if the gaseous fuel and air are introduced into the cylinder when its volume is largest until the pressure is 101.0 KPa. the temperature of both incoming air and fuel is 100∘C. (Assume the fuel to be isoctane , C8H18)View SolutionA wheel of radius R=10cm and moment of inertia I=0.05kgm2 is rotating about a fixed horizontal axis O with angular velocity ω0=10rads−1. A uniform riigid rod of mass m=3kg and length l=50cm is hinged at one end A such that it can rotate at end A in a vertical plane. End B of the rod is tied with a thread as shown in figure such that the rod is horizontal and is just in contact with the surface of rotating wheel. Horizontal distance between axis of rotation O of cylinder and A is equal to a=30cm.
If the wheel stops rotating after one second after the thread has burnt, calculate coefficient of friction ,μ between the rod and the surface of the wheel. (g=10ms−2)
 View Solution
View SolutionFluids at rest exert a normal force to the walls of the container or to the sruface of the Body immersed in the fluid. The pressure exerted by this force at a point inside the liqid is the sum of atmospheric pressure and a factor which depends on the density of the liquid, the acceleration due to gravity and the height of the liquid, above that point. The upthrust acting on a body immersed in a stationary liquid is the net force acting on the body in the upward direction. A number of phenomenon of liquids in motion can be explain by Bernoulli's theorem which relates the pressure, flow speed and height for flow of an ideal incompressible fluid.
A container of large uniform corss sectional area. A resting on a horizontal surface holds two immiscible, non viscous and incompressile liquids of densities d and 2d, each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0.
Situation I:
A homogeneous solid cylinder of length L(L<H/2). cross sectional area A/5 is immersed such that it floats with its axis vertical at liquid -liquid interface with lenght L/4 in the denser liquid.
The density of the solid isView SolutionFluids at rest exert a normal force to the walls of the container or to the sruface of the body immersed in the fluid. The pressure exerted by this force at a point inside the liqid is the sum of atmospheric pressure and a factor which depends on the density of the liquid, the acceleration due to gravity and the height of the liquid, above that point. The upthrust acting on a body immersed in a stationary liquid is the net force acting on the body in the upward direction. A number of phenomenon of liquids in motion can be explain by Bernoulli's theorem which relates the pressure, flow speed and height for flow of an ideal incompressible fluid.
A container of large uniform corss sectional area. A resting on a horizontal surface holds two immiscible, non viscous and incompressile liquids of densities d and 2d, each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0.
Situation I:
A homogeneous solid cylinder of length L(L<H/2). cross sectional area A/5 is immersed such that it floats with its axis vertical at liquid -liquid interface with lenght L/4 in the denser liquid.
The total pressure at the bottom of the container isView Solution
There are two concentric cylinders of radii R1 and R2 as shown. The narrow space between the two cylinders is filled with liquid of viscosity μ. The inner cylinder is held stationary by means of a torsional spring of stiffness G. the outer cylinder is rotated with constant angular speed ω. The torque acting on the inner cylinder due to shearing action of thhe liquid:View Solution

