A cylindrical tank has a hole of diameter 2r in its bottom. The hole i

Find the pressure exerted at the tip of a drawing pin if it is pushed against a board with a force of $20 N .$ Assume the area of the tip to be $0.1 m m^{2} .$

View Solution

Find $\frac{d y}{d x}$ for the following functions: $y = x^{3} - 3 x^{2} + 3 x - (\frac{2}{5})$ .

View Solution

The length of a suspended loire increases by $10^{- 4}$ of its original length when a stress of $10^{7} N m^{- 2}$ is applied on it. Calculate the Young's modulus of the material of the wire.

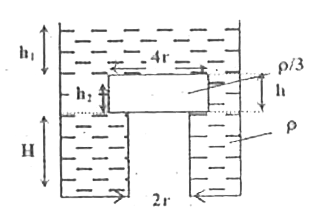
View Solution

A cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density $ρ / 3$ .
ocr_image
Situation I: Initially, the tank is filled with water of density $ρ$ to a height such that the height of water above the top of the block is $h_{1}$ (measured from the top of the block).
Situation II: The water is removed from the tank to a height $h_{2}$ (measured from the bottom of the block), as shown in the figure. The height $h_{2}$ is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the minimum value of height $h_{1}$ (in situation 1), for which the block just starts to move up?

View Solution

A cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density $ρ / 3$ .
ocr_image
Situation I: Initially, the tank is filled with water of density $ρ$ to a height such that the height of water above the top of the block is $h_{1}$ (measured from the top of the block).
Situation II: The water is removed from the tank to a height $h_{2}$ (measured from the bottom of the block), as shown in the figure. The height $h_{2}$ is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the height of the water level $h_{2}$ (in situation 2), for which the block remains in its origin) position whithout the application of any external force

View Solution

A cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density $ρ / 3$ .
ocr_image
Situation I: Initially, the tank is filled with water of density $ρ$ to a height such that the height of water above the top of the block is $h_{1}$ (measured from the top of the block).
Situation II: The water is removed from the tank to a height $h_{2}$ (measured from the bottom of the block), as shown in the figure. The height $h_{2}$ is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
In situation 2, if $h_{2}$ is further decreased, then

View Solution

A cylindrical tank of height H is open at the top end and it has a radius r . Water is filled in it up to a height of h . The time taken to empty the tank through a hole of radius r' in its bottom is

View Solution

A wooden cylinder of diameter 4 r, height H and density rho//3 is kept on a hole of diameter 2 r of a tank, filled with water of density rho as shown in the The block in the above question is maintained by external means and the level of liquid is lowered. The height h_(2) when this external force reduces to zero is

View Solution

A wooden cylinder of diameter 4 r, height H and density $ρ / 3$ is kept on a hole of diameter 2 r of a tank, filled with water of density $ρ$ as shown in the
ocr_image
If height $h_{2}$ of water level is further decreased, then

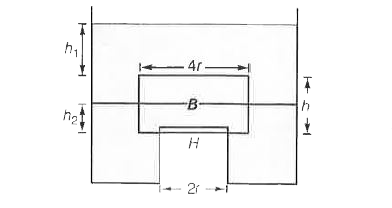
View Solution

A wooden cylindrical of diameter 4r, height h and density $ρ / 3$ is kept on a hole of diameter 2r of a tank , filled with water of density $ρ$ as shown in the figure . The height of the base of cylinder from the base of tank is H .
ocr_image
Let the cylinder is prevented from moving up , by applying a force and water level is further decreased . Then , height of water level ( $h_{2}$ in figure ) for which the cylinder remains in original position without application of force is

View Solution

A cylindrical tank of height 0.4m is open at the top and has a diameter 0.16m. Water is filled in it uo to height of 0.16m. Find the time taken to empty the tank through a hole of radius 5xx10^(-3)m in its bottom.

View Solution

एक बेलनाकार टेंक की तली पर व्यास 2r का छिद्र है। छिद्र को लकड़ी के बेलनाकार गुटके से ढका गया है, जिसका व्यास 4r, ऊँचाई h तथा घनत्व p/3 है।
ocr_image
स्थिति 2 में, यदि $h_{2}$ और घटता है, तब

View Solution

एक टंकी के तल में 2r व्यास का एक बेलनाकार छिद्र H है ( चित्रानुसार)। इस छिद्र से द्रव के बहाव रोकने के लिए इसके ऊपर 4r व्यास h ऊंचाई का एक बेलनाकार ब्लॉक B रखा जाता है। ब्लॉक की सतह से $h_{1}$ ऊंचाई तक द्रव भरा हुआ है। द्रव का घनत्व $ρ$ व् ब्लॉक का घनत्व $ρ / 3$ है।
ocr_image
यदि द्रव की सतह को ओर कम किया जाता है। ब्लॉक की निचली सतह से द्रव के तल की दुरी $h_{2}$ हो तो $h_{2}$ के वह अधिकतम मान जिस पर ब्लॉक पाने स्थान से न हिले

View Solution

एक टंकी के तल में 2r व्यास का एक बेलनाकार छिद्र H है ( चित्रानुसार)। इस छिद्र से द्रव के बहाव रोकने के लिए इसके ऊपर 4r व्यास h ऊंचाई का एक बेलनाकार ब्लॉक B रखा जाता है। ब्लॉक की सतह से $h_{1}$ ऊंचाई तक द्रव भरा हुआ है। द्रव का घनत्व $ρ$ व् ब्लॉक का घनत्व $ρ / 3$ है।
ocr_image
यदि द्रव की सतह को ओर कम किया जाता है। ब्लॉक की निचली सतह से द्रव के तल की दुरी $h_{2}$ हो तो $h_{2}$ के वह अधिकतम मान जिस पर ब्लॉक पाने स्थान से न हिले

View Solution

A cylindrical tank of height $H$ is open at the top end and it has a radius $r$ . Water is filled in it up to a height of $h$ . The time taken to empty the tank through a hole of radius $r'$ in its bottom is

View Solution

A cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density rho//3 . Situation I: Initially, the tank is filled with water of density rho to a height such that the height of water above the top of the block is h_1 (measured from the top of the block). Situation II: The water is removed from the tank to a height h_2 (measured from the bottom of the block), as shown in the figure. The height h_2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere. Find the minimum value of height h_1 (in situation 1), for which the block just starts to move up?

View Solution

Topper's Solved these Questions

Similar Questions

SL ARORA-Mechanical Properties of fluids-Exercise