A force of 100 N is applied horizontally on a block of mass 10 kg placed on a horizontal floor of coefficient of friction 0.5, The acceleration of the block is (takeg=10ms−2)
Zero
5.2ms−2
10ms−2
5ms−2
To solve the problem step by step, we will follow these calculations:
Step 1: Identify the given values
- Force applied (F) = 100 N
- Mass of the block (m) = 10 kg
- Coefficient of friction (μ) = 0.5
- Acceleration due to gravity (g) = 10 m/s²
Step 2: Calculate the normal force (N)
The normal force (N) acting on the block is equal to its weight since the block is on a horizontal surface. The weight (W) can be calculated using the formula:
W=m⋅g
Substituting the values:
N=m⋅g=10kg⋅10m/s2=100N
Step 3: Calculate the frictional force (f)
The frictional force can be calculated using the formula:
f=μ⋅N
Substituting the values:
f=0.5⋅100N=50N
Step 4: Determine the net force (F_net)
The net force acting on the block can be calculated by subtracting the frictional force from the applied force:
Fnet=F−f
Substituting the values:
Fnet=100N−50N=50N
Step 5: Calculate the acceleration (a)
Using Newton's second law of motion, F=m⋅a, we can rearrange it to find acceleration:
a=Fnetm
Substituting the values:
a=50N10kg=5m/s2
Final Answer
The acceleration of the block is 5m/s2.
---
- Force applied (F) = 100 N
- Mass of the block (m) = 10 kg
- Coefficient of friction (μ) = 0.5
- Acceleration due to gravity (g) = 10 m/s²
The normal force (N) acting on the block is equal to its weight since the block is on a horizontal surface. The weight (W) can be calculated using the formula:
W=m⋅g
Substituting the values:
N=m⋅g=10kg⋅10m/s2=100N
The frictional force can be calculated using the formula:
f=μ⋅N
Substituting the values:
f=0.5⋅100N=50N
The net force acting on the block can be calculated by subtracting the frictional force from the applied force:
Fnet=F−f
Substituting the values:
Fnet=100N−50N=50N
Using Newton's second law of motion, F=m⋅a, we can rearrange it to find acceleration:
a=Fnetm
Substituting the values:
a=50N10kg=5m/s2
The acceleration of the block is 5m/s2.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 02EXERCISE - SECTION - A(Answer the following )7videos
SELF ASSESSMENT PAPER 02
- BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 02EXERCISE - SECTION-B (Answer the following )13videos
SELF ASSESSMENT PAPER 02
- BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 01EXERCISE - SECION- D (Answer the following )6videos
SELF ASSESSMENT PAPER 01
- BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 3EXERCISE - Section-D6videos
SELF ASSESSMENT PAPER 3
Similar Questions
A block of mass 20 kg is on a horizontal plane of a coefficient of friction 0.5. by applying 6.0 newton force on it, frictional force will be (g=10m/s2).
View SolutionA force of 49 N just able to move a block of wood weighing 10 kg on a rough horizontal surface , then coefficient of friction is
View SolutionA force of 10N is acting on a block of 20kg on horizontal surface with coefficient of friction μ=0.2. Calculate the work done by the force.
View SolutionA block B is pulled by a force of 18 N applied to a light pulley as shown in the figure. If the coefficient of friction is 0.4 and the acceleration of the block is 0.5 ms−2 , the mass of the block is (g=10m/s2)
 View Solution
View SolutionWhat is the value of applied force ‘F’ which is exerted at an angle θ with the horizontal on a block of mass ‘m’ placed on a horizontal rough surface, if the coefficient of static friction between the block and the surface is , such that the block is on the verge of moving horizontally?
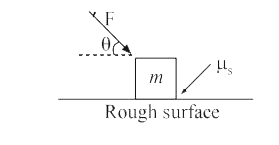 View Solution
View SolutionA force F is acting at an angle θ with horizontal on a block of mass 12 kg placed on a rough 3 horizontal surface having coefficient of friction μ=34 as shown in the figure. The minimum value of force F to just move the block will be (g=10ms−2)
View SolutionA force F is applied on a block of mass √3kg which rests on a horizontal surface with a coefficient of friction 12√3. The maximum value of F for which the block doesn't move, is [Take g=10ms−2]
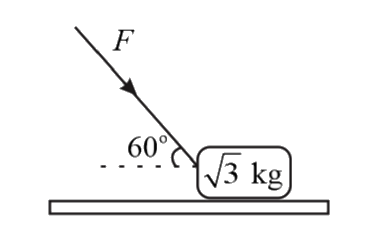 View Solution
View SolutionA block of mass 20kg is pushed with a horizontal force of 90N. If the coefficient of static & kinetic friction are 0.4 & 0.3, the frictional force acting on the block is: (g=10ms−2)
View SolutionA force F is acting at an angle θ with horizontal on a block of mass 12 kg placed on a rough horizontal surface having coefficient of friction μ=34 as shown in the figure. The minimum value of force F to just move the block will be (g=10ms−2)
View SolutionA block of mass 5 kg is placed on a rough horizontal plane . The coefficients of stastic and kinetic friction between the block and surface are 0⋅5and0⋅3 respectively. A force of 100 N is applied at an angle 30∘ with the horizontal as shown in the figure . The acceleration of the block will be [ g = 10m/s2]
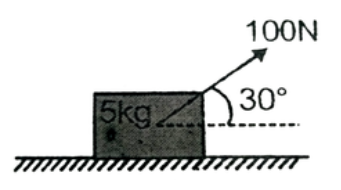 View Solution
View Solution

