A glass hemisphere of radius 10cm and μ=1.5 is silvered over its curved surface. There is an air bubble in the glass 5cms from the plane surface along the axis. Find the position of the images of this bubble seen by observer looking along the axis into the flat surface of the atmosphere.
The correct Answer is:A, C, D
To solve the problem step by step, we will follow the principles of refraction and reflection.
Step 1: Understanding the Setup
We have a glass hemisphere with a radius of 10 cm and a refractive index (μ) of 1.5. An air bubble is located 5 cm from the flat surface of the hemisphere along the axis. The curved surface is silvered, making it act as a mirror.
Step 2: Finding the Apparent Depth of the Bubble
The apparent depth (h') of the bubble when viewed from the air (rarer medium) can be calculated using the formula:
h′=hμ
Where:
- h = actual depth of the bubble = 5 cm
- μ = refractive index of glass = 1.5
Substituting the values:
h′=5 cm1.5=5×23=103≈3.33 cm
This means that the first image of the bubble, as seen by an observer looking into the flat surface, is located approximately 3.33 cm from the flat surface.
Step 3: Finding the Focal Length of the Mirror
The radius of curvature (R) of the hemisphere is given as 10 cm. The focal length (f) of a spherical mirror is given by:
f=R2
Substituting the value:
f=10 cm2=5 cm
Step 4: Locating the Object Relative to the Mirror
The bubble is located 5 cm from the flat surface, which is also the same distance from the silvered curved surface (mirror). Since the object (bubble) is at the focal point of the mirror (5 cm), we can analyze the image formation.
Step 5: Image Formation by the Mirror
When the object is located at the focal point of a concave mirror, the image formed is at infinity. Thus, the second image of the bubble, as seen by the observer, is formed at infinity.
Final Answer
1. The first image of the bubble is located at approximately 3.33 cm from the flat surface.
2. The second image of the bubble is formed at infinity.
We have a glass hemisphere with a radius of 10 cm and a refractive index (μ) of 1.5. An air bubble is located 5 cm from the flat surface of the hemisphere along the axis. The curved surface is silvered, making it act as a mirror.
The apparent depth (h') of the bubble when viewed from the air (rarer medium) can be calculated using the formula:
- h = actual depth of the bubble = 5 cm
- μ = refractive index of glass = 1.5
The radius of curvature (R) of the hemisphere is given as 10 cm. The focal length (f) of a spherical mirror is given by:
The bubble is located 5 cm from the flat surface, which is also the same distance from the silvered curved surface (mirror). Since the object (bubble) is at the focal point of the mirror (5 cm), we can analyze the image formation.
When the object is located at the focal point of a concave mirror, the image formed is at infinity. Thus, the second image of the bubble, as seen by the observer, is formed at infinity.
1. The first image of the bubble is located at approximately 3.33 cm from the flat surface.
2. The second image of the bubble is formed at infinity.
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 2 Comprehension Based
3 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
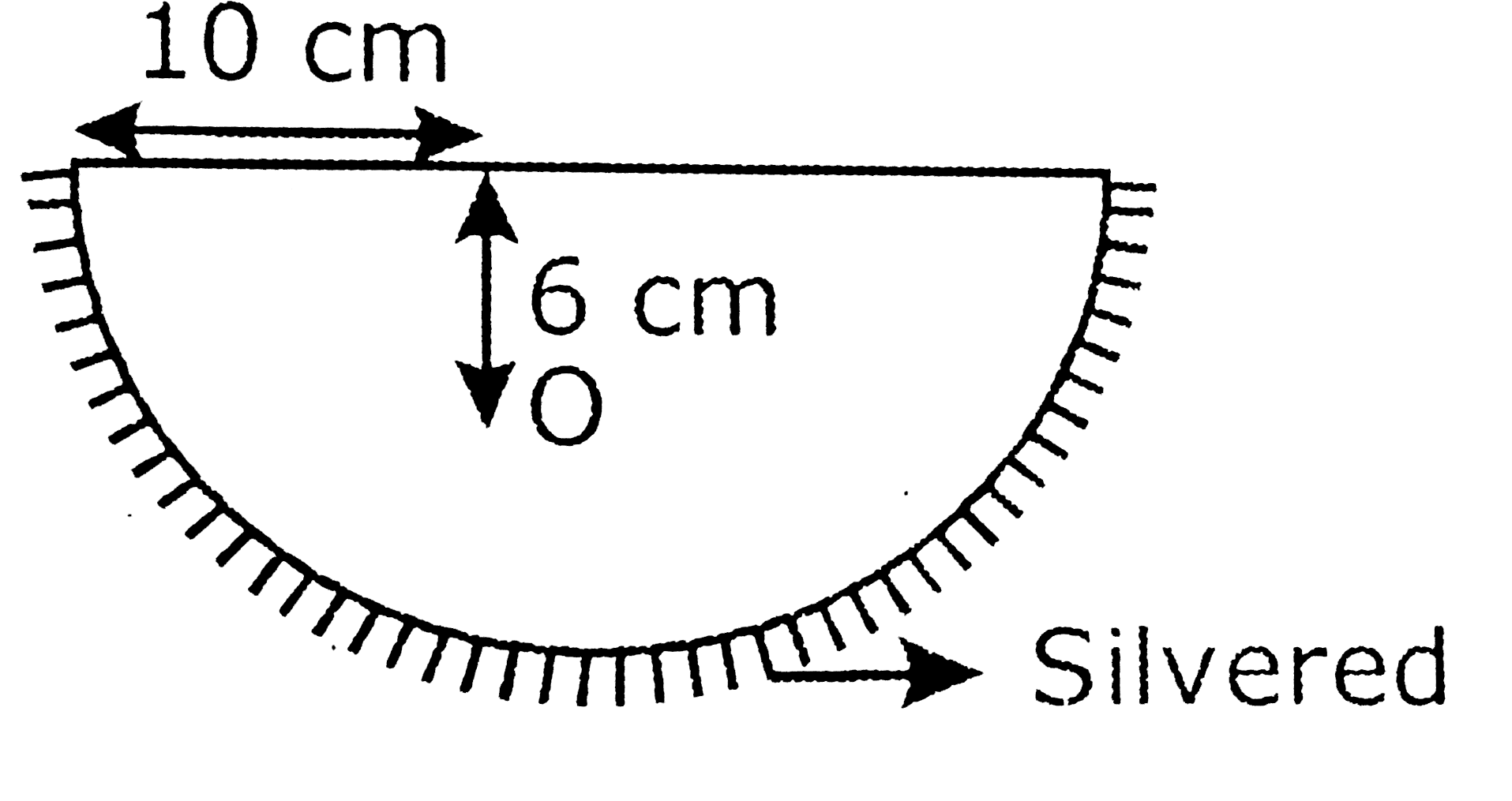
A hemispherical glass body of radius 10 cm and refractive index 1.5 is silvered on its curved surface . A small air bubble is 6 cm below the flat surface inside it along the axis. The position of the image of the air bubble made by the mirror is seen :
View SolutionA small air bubble in a sphere of glass with radius 4 cm appears to be 1 cm from the surface when observed along a diameter. Find the true positino of the air bubble.
View SolutionA glass sphere of diameter 50 cm and μ=1.5 has a small air bubble. Looking from outside the diameter, the bubble appears to be at a distance 10 cm the surface. Find the apparent position of the bubble when it is viewed from the diametrically opposite position.
View SolutionAn object is at a distance of d=2.5cm from the surface of a glass sphere with a radius R=10cm. Find the position of the final image produced by the sphere. The refractive index of glass is μ=1.5.
View SolutionA paraxial beam is incident on a glass (n=1.5) hemisphere of radius R=6 cm in air as shown. The distance of point convergence F from the plane surface of hemisphere is :-
_E01_026_Q01.png)
View SolutionA plastic hemisphere has a radius of curvature of 8 cm and an index of refraction of 1.6. ON the axis halfway between the plane surface and the spherical one (4 cm from each) is a small object O. The distance between the two images when viewed along the axis from the two sides of the hemisphere is approximately
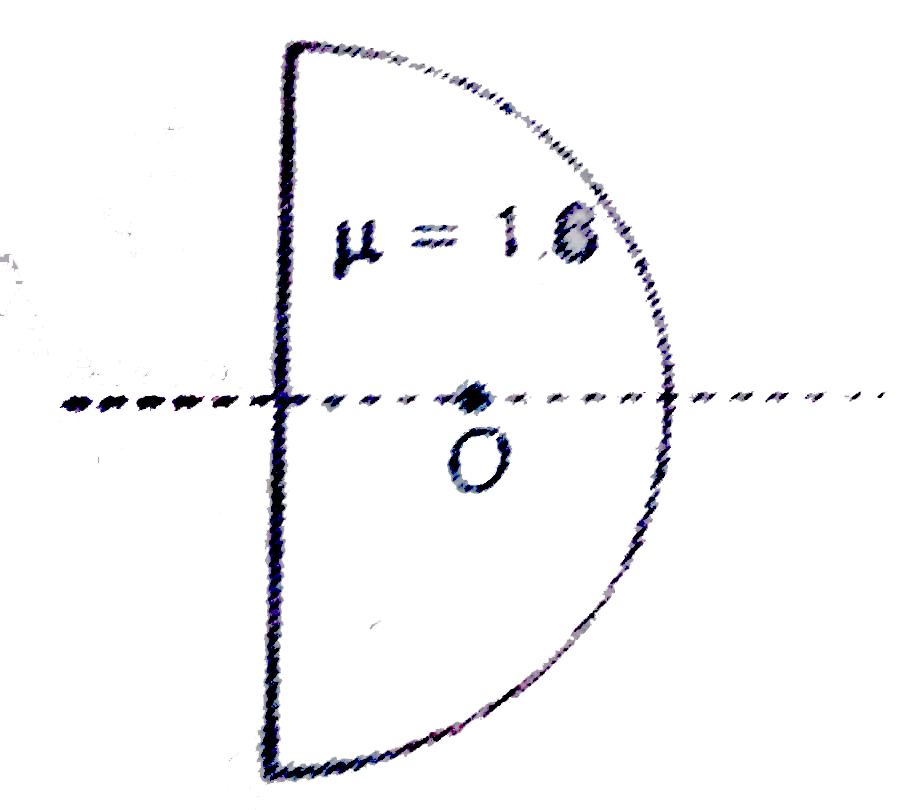
View SolutionA plastic hemisphere has a radius of curvature of 8cm and an index of refraction of 1.6. On the axis halfway between the plane surface and the spherical one (4cm from each) is a small object O.
The distance between the two images when viewed along the axis from the two sides of the hemisphere is approximately.

View SolutionAs an air bubble rises from the bottom of a lake to the surface, its volume is doubled. Find the depth of the lake. Take atmospheric pressure = 76 cm of Hg.
View SolutionA solid glass hemisphere of density d and radius R lies (with curved surface of hemisphere below the flat surface) at the bottom of a tank filled with water of density ρ such that the flat surface of hemisphere is H depth below the liquid surface. Weight of water + tank is W1 and that of hemisphere is'W2. W Then choose the incorrect options
View SolutionA plane mirror is made of glass slab (μg=1.5) 2.5 cm thick and silvered on back. A point object is placed 5 cm in front of the unsilvered face of the mirror. What will be the position of final image ?
View Solution
