A hemispherical shell is uniformly charge positively .the electric field at point on a diameter away from the centre is directed
perpendicular to the diameter
parallel to the diameter
at an angle tilted towards the diameter
at an angle tilted away from the diameter
The correct Answer is:A
To solve the problem of determining the direction of the electric field at a point on the diameter of a uniformly positively charged hemispherical shell, we can follow these steps:
Step 1: Understand the Configuration
We have a hemispherical shell that is uniformly charged with positive charge. Visualize the shell as the upper half of a sphere, and we are interested in a point located on the diameter of this hemisphere, away from its center.
Hint: Visualize the hemispherical shell and the point on the diameter to understand the geometry involved.
Step 2: Analyze the Electric Field Contribution
The electric field due to a positive charge is directed away from the charge. At any point on the diameter, the electric field contributions from different parts of the shell will vary based on their distance and angle relative to the point of interest.
Hint: Remember that electric field lines from positive charges always point away from the charge.
Step 3: Consider Symmetry
Due to the symmetry of the hemispherical shell, for every small charge element on one side of the diameter, there is an equal charge element on the opposite side that contributes to the electric field at the point. The horizontal components (parallel to the diameter) of these electric fields will cancel each other out.
Hint: Use symmetry to simplify the problem. Components of the electric field that are equal and opposite will cancel.
Step 4: Identify the Resultant Electric Field Direction
Since the horizontal components cancel, only the vertical components (perpendicular to the diameter) will add up. Thus, the resultant electric field at the point on the diameter will be directed away from the shell and perpendicular to the diameter.
Hint: Focus on the components of the electric field that do not cancel out; this will help you determine the net direction.
Step 5: Conclusion
The electric field at the point on the diameter away from the center of the hemispherical shell is directed perpendicular to the diameter.
Final Answer: The electric field at a point on the diameter away from the center of the positively charged hemispherical shell is directed perpendicular to the diameter.
We have a hemispherical shell that is uniformly charged with positive charge. Visualize the shell as the upper half of a sphere, and we are interested in a point located on the diameter of this hemisphere, away from its center.
The electric field due to a positive charge is directed away from the charge. At any point on the diameter, the electric field contributions from different parts of the shell will vary based on their distance and angle relative to the point of interest.
Due to the symmetry of the hemispherical shell, for every small charge element on one side of the diameter, there is an equal charge element on the opposite side that contributes to the electric field at the point. The horizontal components (parallel to the diameter) of these electric fields will cancel each other out.
Since the horizontal components cancel, only the vertical components (perpendicular to the diameter) will add up. Thus, the resultant electric field at the point on the diameter will be directed away from the shell and perpendicular to the diameter.
The electric field at the point on the diameter away from the center of the hemispherical shell is directed perpendicular to the diameter.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Assertion And Reason
15 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - NCERT Exemplar
5 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Assertion And Reason
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - NCERT Exemplar
6 Videos
Similar Questions
Knowledge Check
Consider a thin spherical shell of radius R consisting of uniform surface charge density σ. The electric field at a point of distance x from its centre and outside the shell is
Ainversely proportional to σBdirectly proportional to x2Cdirectlr proportional to RDinversely proportional to x2
A hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
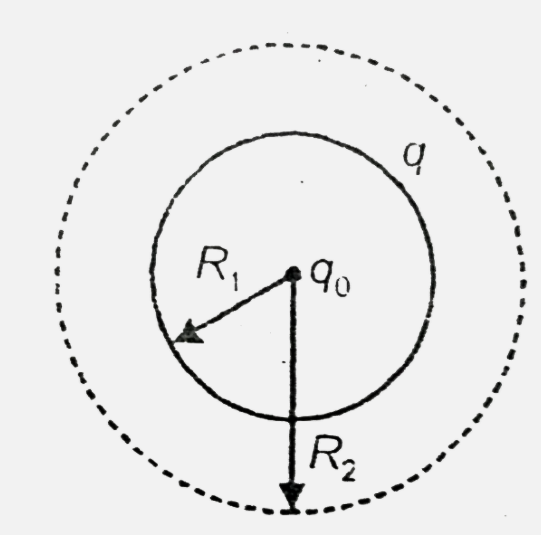
View SolutionA sperical shell is uniformly charged by a charge q. A point charge q0 is at its centre , then
View SolutionIf the potential at the centre of a uniformly charged hollow sphere of radius R is V, then electric field at a distance r from the centre of sphere will be (r>R).

View SolutionA point charge Q is placed at the centre of a spherical conducting shell. A total charge of -q is placed on the shell. The magnitude of the electric field at point P1 at a distance R1 from the centre is X. The magnitude of the electric field due to induced charges at point P2 a distance R2 from the centre is Y. The values of X and Y are respectively.

View SolutionA circular ring carries a uniformly distributed positive charge .The electric field(E) and potential (V) varies with distance (r ) from the centre of thr ring along its axis as

View SolutionFigure shows a uniformly charges hemispherical shell. The direction of electric field at point p that is off centre (but in the plane of the largest circle of the hemisphere), will be along

View SolutionThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View Solution
