A hollow copper sphere is placed in front of a point charge Q such that the latter is at a distance r from the centre O of the former. What is the electric field at the centre O, due to the charges induced in the sphere?
The correct Answer is:14π∈0Qr2
To find the electric field at the center O of a hollow copper sphere due to the charges induced in the sphere by a point charge Q placed at a distance r from the center, we can follow these steps:
1. Understanding the Setup:
- We have a hollow copper sphere and a point charge Q located at a distance r from the center O of the sphere. The copper sphere is a conductor.
2. Induction of Charges:
- When the point charge Q is brought near the hollow copper sphere, it induces charges on the surface of the sphere. Since the sphere is a conductor, free electrons will move in response to the electric field created by the point charge Q.
3. Distribution of Induced Charges:
- The induced charges will redistribute themselves on the surface of the sphere. The side of the sphere facing the charge Q will have a negative charge induced, while the opposite side will have a positive charge induced. This is due to the attraction of electrons towards the point charge Q.
4. Electric Field Inside the Hollow Sphere:
- Inside a conductor in electrostatic equilibrium, the electric field is zero. Therefore, at the center O of the hollow sphere, the electric field due to the induced charges on the sphere itself is zero.
5. Electric Field Due to the Point Charge:
- The electric field due to the point charge Q at the center O of the sphere can be calculated using the formula:
E=kQr2
- However, since we are interested in the electric field at the center O due to the induced charges, we note that the induced charges create an electric field that cancels out the field due to the point charge Q.
6. Resultant Electric Field:
- The electric field due to the induced charges at the center O will be equal in magnitude but opposite in direction to the electric field due to the point charge Q. Hence, the resultant electric field at the center O due to the induced charges is:
Einduced=−kQr2
7. Final Conclusion:
- Therefore, the electric field at the center O due to the charges induced in the sphere is:
Einduced=kQr2(directed towards the point charge Q)
- We have a hollow copper sphere and a point charge Q located at a distance r from the center O of the sphere. The copper sphere is a conductor.
- When the point charge Q is brought near the hollow copper sphere, it induces charges on the surface of the sphere. Since the sphere is a conductor, free electrons will move in response to the electric field created by the point charge Q.
- The induced charges will redistribute themselves on the surface of the sphere. The side of the sphere facing the charge Q will have a negative charge induced, while the opposite side will have a positive charge induced. This is due to the attraction of electrons towards the point charge Q.
- Inside a conductor in electrostatic equilibrium, the electric field is zero. Therefore, at the center O of the hollow sphere, the electric field due to the induced charges on the sphere itself is zero.
- The electric field due to the point charge Q at the center O of the sphere can be calculated using the formula:
E=kQr2
- However, since we are interested in the electric field at the center O due to the induced charges, we note that the induced charges create an electric field that cancels out the field due to the point charge Q.
- The electric field due to the induced charges at the center O will be equal in magnitude but opposite in direction to the electric field due to the point charge Q. Hence, the resultant electric field at the center O due to the induced charges is:
Einduced=−kQr2
- Therefore, the electric field at the center O due to the charges induced in the sphere is:
Einduced=kQr2(directed towards the point charge Q)
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-I)13videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Exercise57videos
ELECTRIC CHARGES AND FIELDS
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Additional Exercise11videos
ELECTROMAGNETIC INDUCTION
Similar Questions
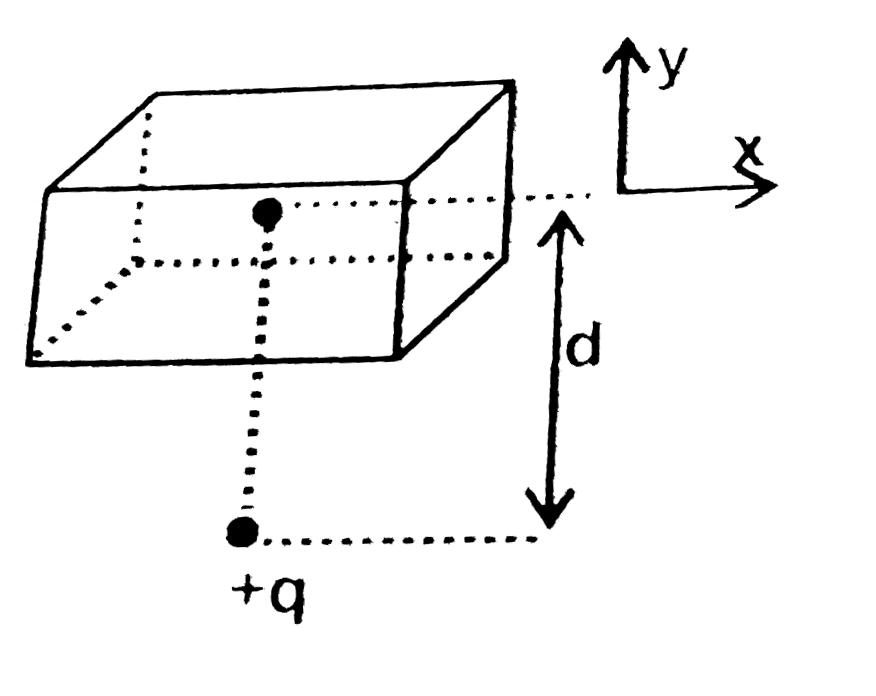
A positive charge q is placed in front of conducting solid cube at a distance d from its centre. Find the electric field at the centre of the cube due to the charges appearing on its surface.
View SolutionA charge +q is placed at a distance 'd' from the centre of the uncharged metallic cube of side 'a'. The electric field at the centre of the cube due to induced charges on the cube will be
 View Solution
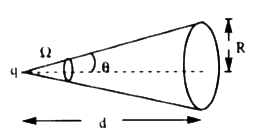
View SolutionA point charge q is placed at a distance d from the centre of a circular disc of radius R. Find electric flux flowing through the disc due to that charge
 View Solution
View SolutionA positive point charge q is placed at a distance 2 R from the surface of a metallic shell of radius R. the electric field at centre of shell due to indouced charge has magnitude
 View Solution
View SolutionA solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :
 View Solution
View SolutionA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View SolutionFigure shows a uniformly charged sphere of radius R and total charge Q. A point charge q is situated outside the sphere at a distance r from centre of sphere. Find out the following :
(i) Force acting on the point charge q due to the sphere.
(ii) Force acting on the sphere due to the point charge.
 View Solution
View SolutionA hollow metal sphere of radius 5 cm is charged such that the potential on its surface is 10V. The potential at the distance 3cm from the centre of the sphere is:
View SolutionA hollow charged metal sphere has radius r. If the potential difference between its surface and a point at a distance 3r from the centre is V, then electric field intensity at a distance 3r is
View SolutionA sphere of radius R carries charge such that its volume charge density is proportional to the square of the distance from the centre. What is the ratio of the magnitude of the electric field at a distance 2 R from the centre to the magnitude of the electric field at a distance of R/2 from the centre?
View Solution
