A hollow vertical cylinder of radius R is rotated with angular velocity ω about an axis through its centre. What is the minimum coefficient of static friction between block M and cylinder wall necessary to keep the block suspended on the inside of the cylinder ?
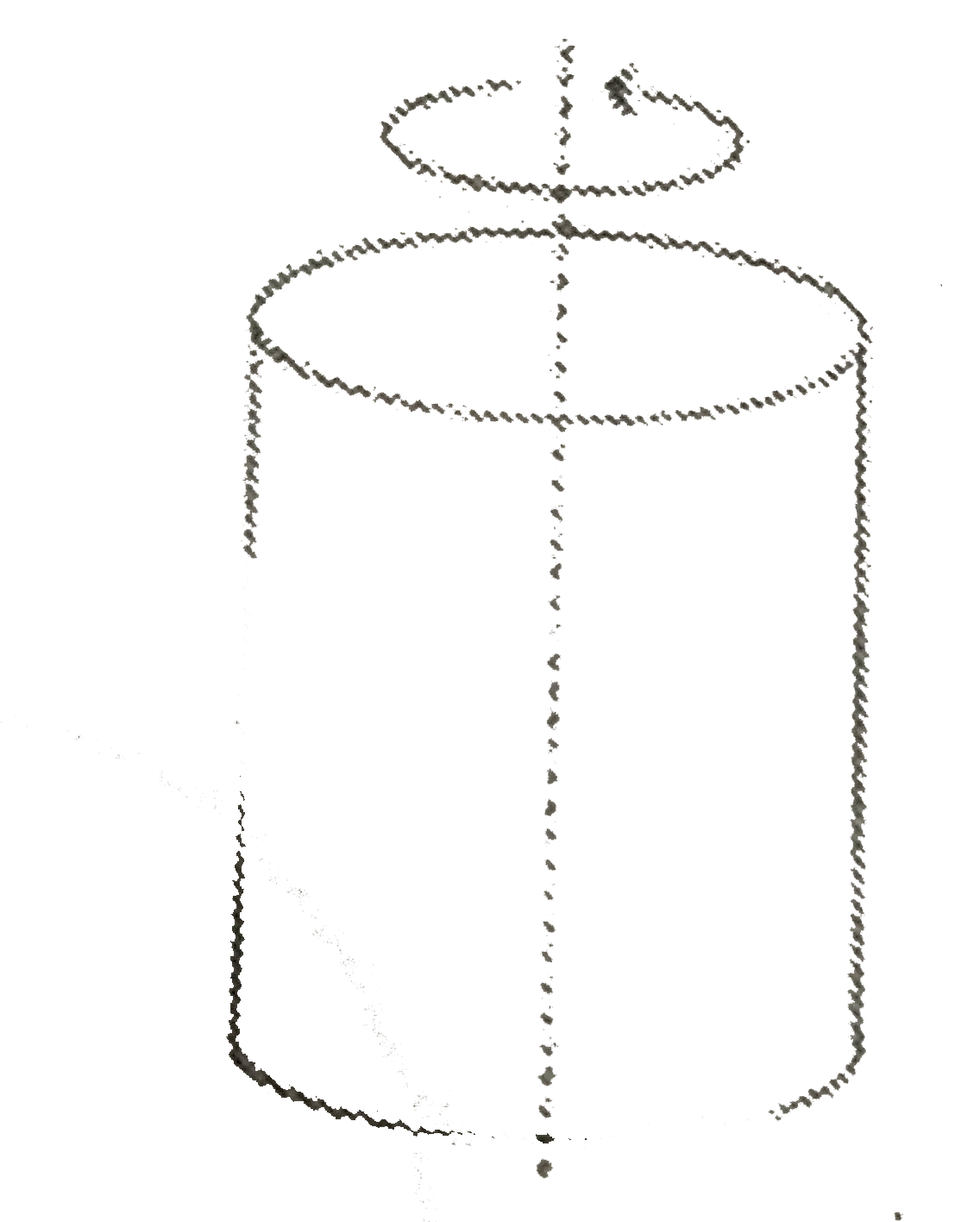
μ=gRω2
μ=ω2gR
μ=ω2Rg
μ=gω2R
The correct Answer is:D
Step by step video, text & image solution for A hollow vertical cylinder of radius R is rotated with angular velocity omega about an axis through its centre. What is the minimum coefficient of static friction between block M and cylinder wall necessary to keep the block suspended on the inside of the cylinder ? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - JEE Advanced
25 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - More than One Option is Correct
13 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Subjective Questions
2 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A uniform cylinder of radius R is spinned about it axis to the angular velocity ω0 and then placed into a corner,. The coeficient of friction between the corner walls and the cylinder is μk How many turns will the cylinder accomplish before it stops?

View SolutionIn the arrangement shown in figure the cylinder of mass M is at rest on an incline. The string between the cylinder and the pulley (P) is horizontal. Find the minimum coefficient of friction between the incline and the cylinder which can keep the system in equilibrium. Also find the mass of the block. Assume no friction between the pulley (P) and the string.
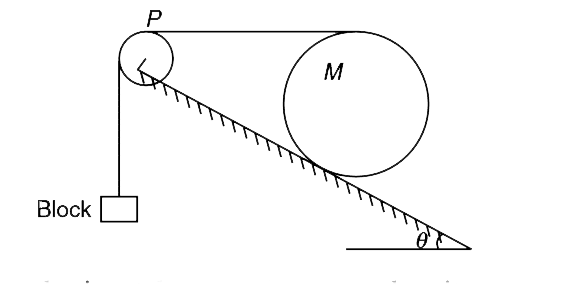
View Solution
Knowledge Check
The moment of inertia of a cylinder of radius R, length L and mass M about an axis passing through its centre of mass and normal to its length is
AML212BMR24CM[L212+R24]DM[L212+R22]A solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2An cylinder of mass m is rotated about its axis by an angular velocity ω and lowered gently on an inclined plane as shown in figure. Then :
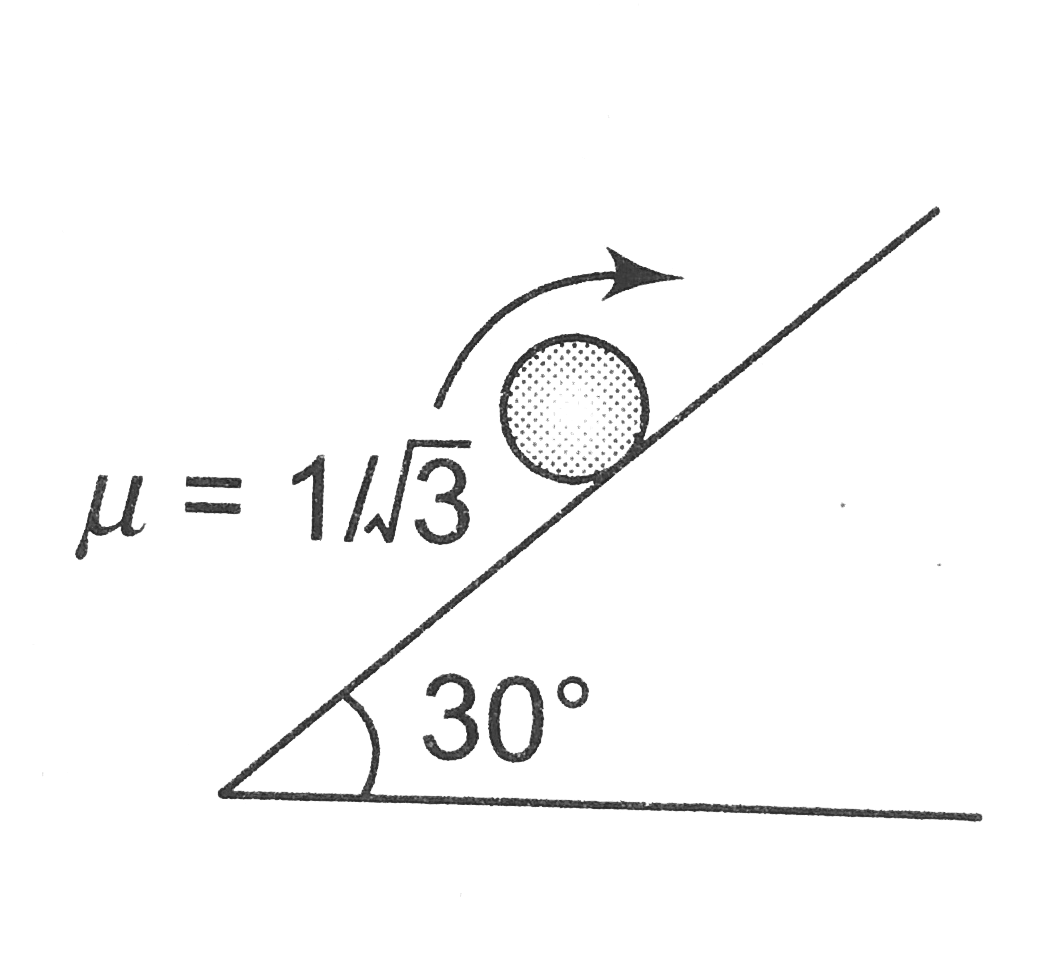 .Ait will start going upwardBit will first going upward and then downwardCit will go downward just after it is loweredDit can never go upward.
.Ait will start going upwardBit will first going upward and then downwardCit will go downward just after it is loweredDit can never go upward.
A solid sphere of radius r and mass m rotates about an axis passing through its centre with angular velocity ω. Its K.E. Is
View SolutionA cylinder with radius R spins about its horizontal axis with angular speed ω. There is a small block lying on the inner surface of the cylinder. The coefficient of friction between the block and the cylinder is μ. Find the value of ω for which the block does not slip, i.e., stays at rest with respect to the cylinder.
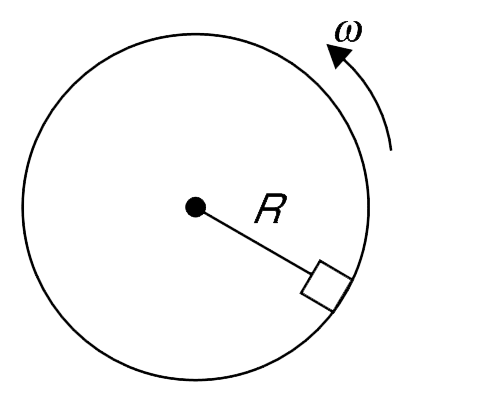
View SolutionA uniform cylinder of the radius R ( = 3 m) is spin about its axis at an angular velocity ω0(=40√π rad s−1) and placed between two perpendicular walls. The coefficient of friction between the walls and cylinder is μ(=2). Then, how many rotations will the cylinder make before it comes to rest?
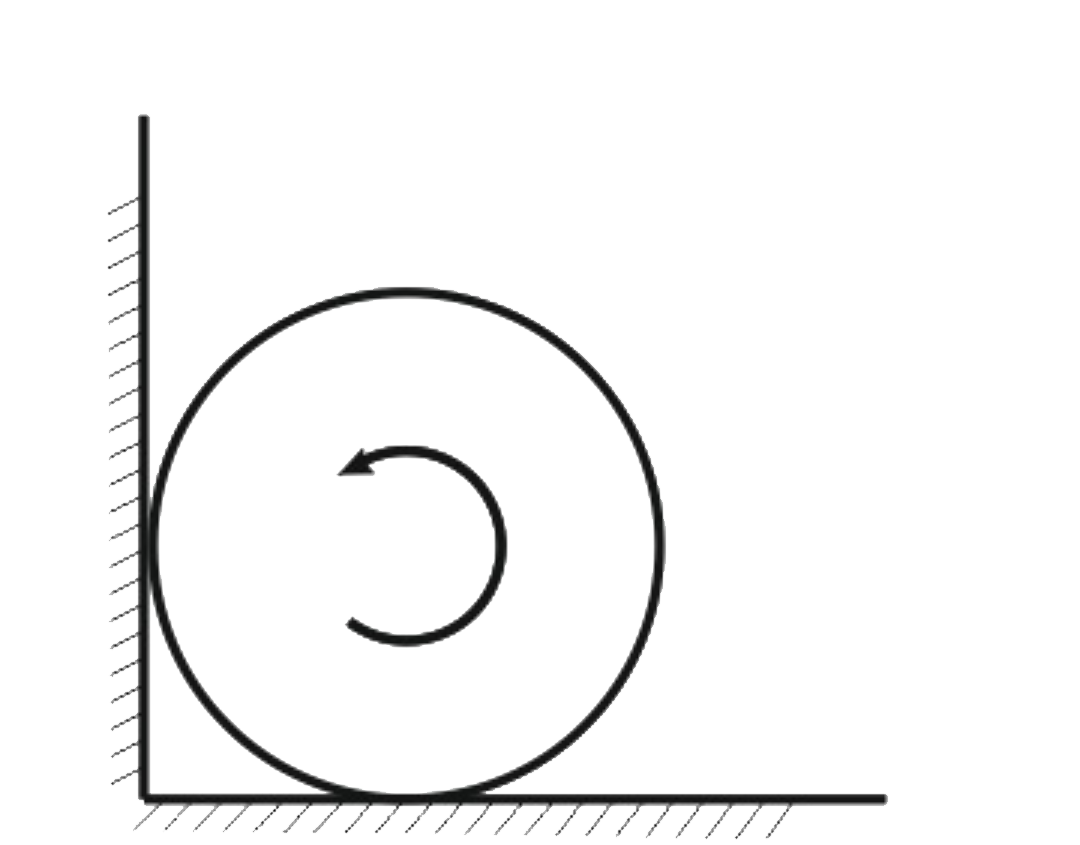
View SolutionA uniform solid cylinder of mass m and radius R is set in rotation about its axis with an angular velocity ω0, then lowered with its lateral surface onto a horizontal plane and released. The coefficient of friction between the cylinder and the plane is equal to μ. Find
(a) how long the cylinder will move with sliding,
(b) the total work performed by the sliding friction force acting on the cylinder.
View SolutionA solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
View Solution
