A horizontal force F is applied on a uniform sphere of radius r and weight W and as a result, the sphere slides over the horizontal table. If the coefficient of friction between the sphere and the table is μ, then show that h =r(1−μWF).
The point of contact between the table and the sphere is Q. Here, the force of friction f acts along the surface of the table through the point Q opposite to the force F. The weight of the sphere W acts vertically downwards through the centre of the sphere. Since the sphere slides over the horizontal table it has no rotational motion.
So, with respect to the centre O,
f×r=F(r−h) or, μW×r=F(r−h)
h=r(1−μWF).

Topper's Solved these Questions
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS
18 Videos
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - EXERCISE (Multiple Choice Questions )
14 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - CBSE SCANNER
16 Videos
- SUPERPOSITION OF WAVESBOOK - CHHAYA PUBLICATIONCHAPTER - SUPERPOSITION OF WAVESEXERCISE - CBSE Scanner
14 Videos
Similar Questions
A hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
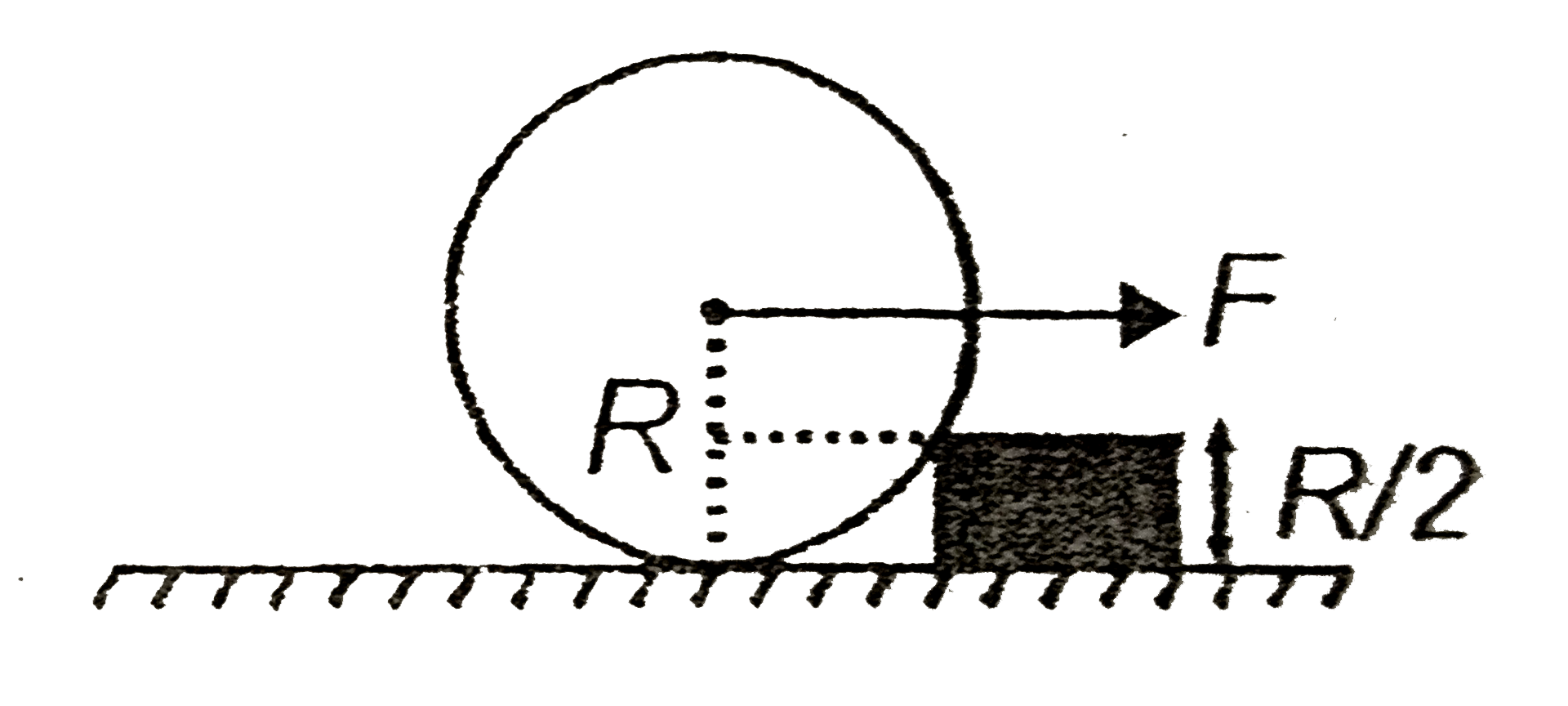
View SolutionThe minimum horizontal force applied to the centre of wheel of radius R and weight w to pull it over a step of height R/2
View Solution
Knowledge Check
A hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
AFriction opposes its translationBFriction supports rotation motionCOn decreasing θ, frictional force decreasesDAll of theseA solid sphere of mass m is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is μ. The maximum value of F, so that the sphere will not slip, is equal to
 A75μmgB47μmgC57μmgD72μmg
A75μmgB47μmgC57μmgD72μmgA solid sphere of mass m is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is μ. The maximum value of F, so that the sphere will not slip, is equal to
 A75μmgB47μmgC57μmgD72μmg
A75μmgB47μmgC57μmgD72μmg
The minimum horizontal force applied to the centre of wheel of radius R and weight w to pull it over a step of height R/2

View Solution25% of a uniform chain hangs from the edge of a horizontal table top. If the chain is on the verge of sliding,the coefficient of static friction between the chain and horizontal table is
View SolutionA solid sphere of mass m is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is μ. The maximum value of F, so that the sphere will not slip, is equal to

View SolutionA uniform solid sphere of radius r is rolling on a smooth horizontal surface with velocity v and angular velocity ω=(v=ωr). The sphere collides with a sharp edge on the wall as shown in figure. The coefficient of friction between the sphere and the edge μ=1/5. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the surface just after the collision is equal to

View Solution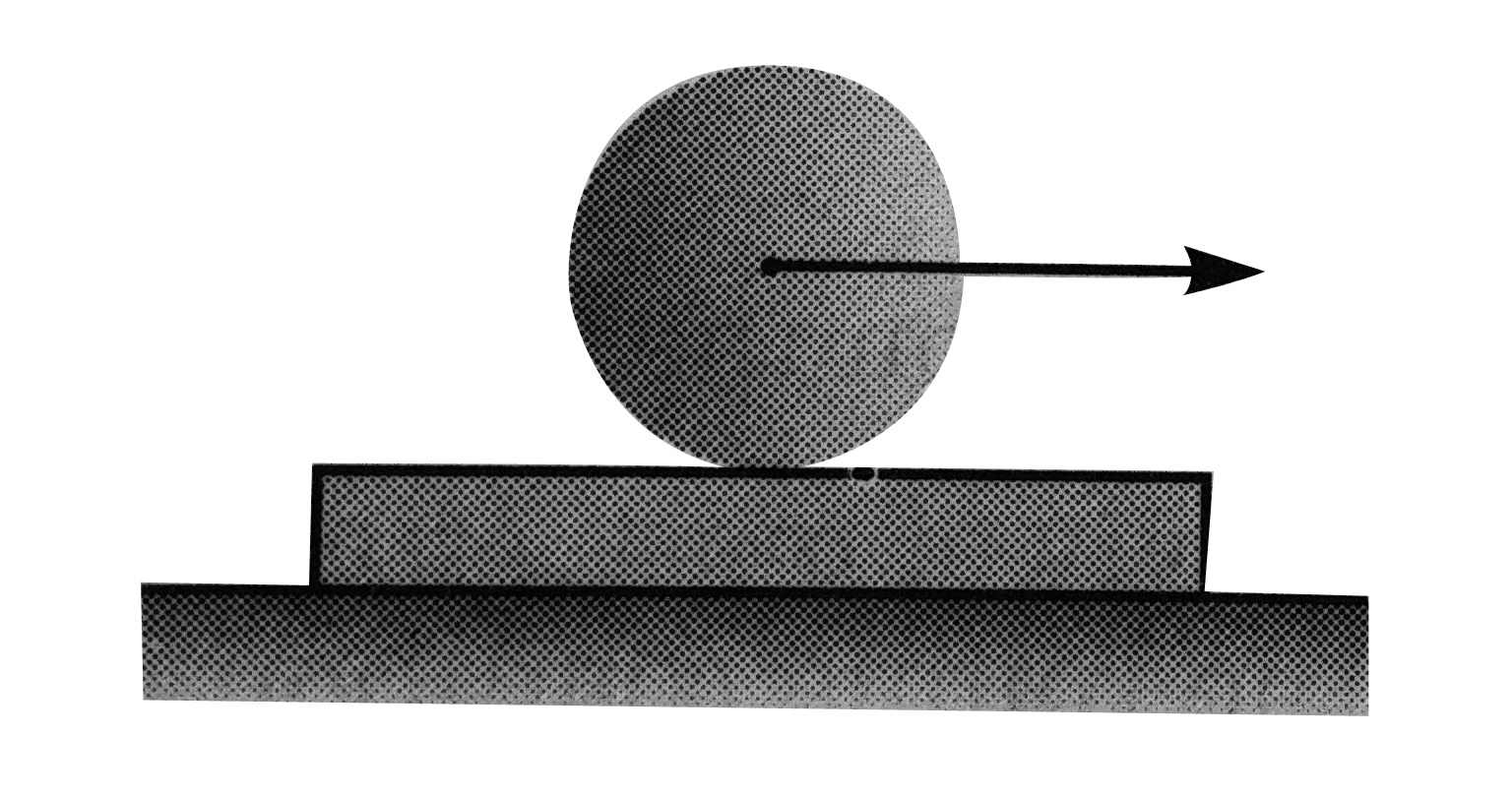
A horizontal force F is applied at the centre of solid sphere placed over a plank. The minimum coefficient of friction between plank and sphere required for pure rolling is μ1 when plank is kept at rest ad μ2 when plank can move, then μ2<μ1
Reason: Work done by frictional force on the sphere in both cases is zero.
View Solution
