A jet aeroplane is flying at a constant height of 2 km with a speed 360kmh−1 above the ground towards a target and releases a bomb. After how much time it will hit the target and what will be the horizontal distance of the aeroplane from the target so that the bomb should hit the target ? (Take g=10ms−2)
10s, 1km
20 s, 2km
30s, 3km
40s, 4km
The correct Answer is:B
To solve the problem step by step, we will break it down into two parts: calculating the time it takes for the bomb to hit the target and then determining the horizontal distance from the aeroplane to the target.
Step 1: Convert the speed of the aeroplane from km/h to m/s
The speed of the aeroplane is given as 360 km/h. We need to convert this to meters per second (m/s).
Speed in m/s=360 km1 h×1000 m1 km×1 h3600 s=360×10003600=100 m/s
Step 2: Calculate the time taken for the bomb to hit the ground
The bomb is released from a height of 2 km (2000 m). We will use the second equation of motion to find the time taken for the bomb to fall to the ground.
The equation is:
s=ut+12at2
Where:
- s=2000 m (the height)
- u=0 m/s (initial vertical velocity)
- a=g=10 m/s2 (acceleration due to gravity)
Substituting the values into the equation:
2000=0⋅t+12⋅10⋅t2
This simplifies to:
2000=5t2
t2=20005=400
t=√400=20 seconds
Step 3: Calculate the horizontal distance from the aeroplane to the target
Now that we have the time, we can find the horizontal distance using the formula:
Horizontal Distance=Horizontal Velocity×Time
Where:
- Horizontal Velocity vx=100 m/s
- Time t=20 seconds
Substituting the values:
Horizontal Distance=100 m/s×20 s=2000 m=2 km
Final Results
- The time taken for the bomb to hit the target is 20 seconds.
- The horizontal distance from the aeroplane to the target is 2 km.
The speed of the aeroplane is given as 360 km/h. We need to convert this to meters per second (m/s).
The bomb is released from a height of 2 km (2000 m). We will use the second equation of motion to find the time taken for the bomb to fall to the ground.
s=ut+12at2
Where:
- s=2000 m (the height)
- u=0 m/s (initial vertical velocity)
- a=g=10 m/s2 (acceleration due to gravity)
2000=0⋅t+12⋅10⋅t2
This simplifies to:
2000=5t2
t2=20005=400
t=√400=20 seconds
Now that we have the time, we can find the horizontal distance using the formula:
Horizontal Distance=Horizontal Velocity×Time
Where:
- Horizontal Velocity vx=100 m/s
- Time t=20 seconds
Horizontal Distance=100 m/s×20 s=2000 m=2 km
- The time taken for the bomb to hit the target is 20 seconds.
- The horizontal distance from the aeroplane to the target is 2 km.
Topper's Solved these Questions
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - B. Medical entrance
1 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrance
12 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - A. Taking it together
1 Videos
- MEASUREMENT AND ERRORSBOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective
19 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
Similar Questions
An aeroplane is flying at a constant height of 1960 m with speed 600kmh−1 above the ground towards point directly over a person struggling in flood water. At what angle of sight with the vertical should be pilot release a survival kit if it is to reach the person in water ? (g=9.8ms−2)
View SolutionAn aeroplane flying horizontally at an altitude of 490m with a speed of 180 kmph drops a bomb. The horizontal distance at which it hits the ground is
View Solution
Knowledge Check
An aeroplane flying horizontally with a speed of 360 km h−1 releases a bomb at a height of 490 m from the ground. If g = 9. 8 m s−2 , it will strike the ground at
A10 kmB100 kmC1 kmD16 kmA fighter plane flying horizontally at an altitude of 1.5km with speed 720kmh−1 passes directly over head an anticraft gun.
At what angle from the vertical should the gun be fired from the shell with muzzle speed 600ms−1 to hit plane.
At what minimum altitude should the pilot fly the plane to avoid being hit ? ( Take g= 10 ms−2).Asin−1(13) , 16kmBsin−1(23) ,16 kmCcos−1(13) 16mDcos−1(23) ,16m
A bulley with muzzle velocity 100ms−1 is to be shot at a target 30m away in the same horizontal line. How high above the target must the rifle be aimed so that the bullet will hit the target ?
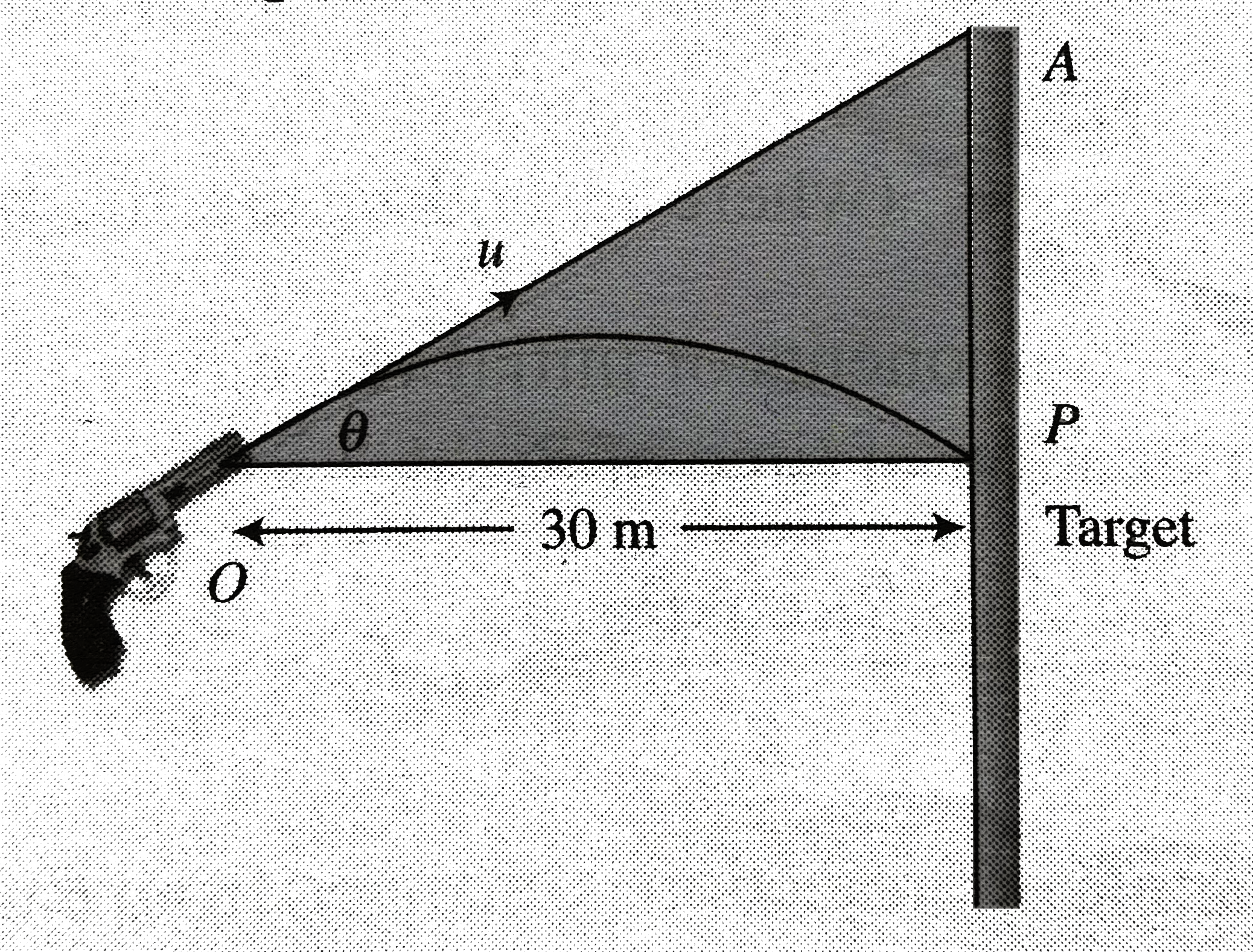 .
.
View SolutionA fighter plane is flying horizontally at an altitude of 1.5 km with speed 720kmh−1. At what angle of sight (w.r.t horizontal) when the target is seen, should the pilot drop the bomb in order to attack the target? (Takeg=10ms−2)
View SolutionA bomb is released from an aeroplane flying at a speed of 720km/h in the horizontal direction 8000m above the ground. At what horizontal distance from the initial position of areoplane it strikes the ground.
View SolutionA fighter plane flying horizontally at an altitude of 1.5 km with speed 720 km h−1 passes diretly overhead an anti-aircraft gun. At what angle from the vertical should the gun he fired for the shell with muzzle speed 600 m s−1 to hit the plane. (Take g = 10 m s−1)
View SolutionA stone is thrown with a speed of 10ms−1 at an angle of projection 60∘. Find its height above the point of projection when it is at a horizontal distance of 3m from the thrower ? (Take g=10ms−2)
View SolutionA stone is thrown with a speed of 10ms−1 at an angle of projection 60∘. Find its height above the point of projection when it is at a horizontal distance of 3m from the thrower ? (Take g=10ms−2)
View Solution
