A light ray is incident on a transparent slab of refractive index μ=√2 at an angle of incidence π/4. Find the ratio of the lateral displacement suffered by the light ray to the maximum value which it could have suffered.
√3−1√6
√3−2√5
√1−2√5
√1−2√7
The correct Answer is:A
To solve the problem, we need to find the lateral displacement of a light ray passing through a transparent slab and then calculate the ratio of this displacement to its maximum possible value. Here’s the step-by-step solution:
Step 1: Understand the parameters given
- Refractive index of the slab, μ=√2
- Angle of incidence, i=π4 (which is 45 degrees)
Step 2: Use Snell's Law to find the angle of refraction
According to Snell's Law:
μ=sinisinr
Substituting the values we have:
√2=sin(π4)sinr
Since sin(π4)=√22:
√2=√22sinr
Rearranging gives:
sinr=√22√2=12
Thus, r=π6 (which is 30 degrees).
Step 3: Calculate the lateral displacement x
The formula for lateral displacement x through a slab is given by:
x=t⋅sini−sinrcosr
Where t is the thickness of the slab. We can express sini and sinr:
- sini=sin(π4)=√22
- sinr=sin(π6)=12
- cosr=cos(π6)=√32
Substituting these values into the formula:
x=t⋅√22−12√32=t⋅√2−12√32=t⋅√2−1√3
Step 4: Find the maximum lateral displacement
The maximum lateral displacement occurs when the angle of incidence is such that the light ray is incident normally (i.e., i=90∘). In this case, the maximum lateral displacement xmax can be calculated as:
xmax=t⋅sinicosr
Since sin(90∘)=1:
xmax=t⋅1cosr=t⋅1√32=2t√3
Step 5: Calculate the ratio of lateral displacement to maximum displacement
Now we find the ratio:
Ratio=xxmax=t⋅√2−1√32t√3
Cancelling t and √3:
Ratio=√2−12
Final Answer
The ratio of the lateral displacement suffered by the light ray to the maximum value which it could have suffered is:
√2−12
- Refractive index of the slab, μ=√2
- Angle of incidence, i=π4 (which is 45 degrees)
According to Snell's Law:
μ=sinisinr
Substituting the values we have:
√2=sin(π4)sinr
Since sin(π4)=√22:
√2=√22sinr
Rearranging gives:
sinr=√22√2=12
Thus, r=π6 (which is 30 degrees).
The formula for lateral displacement x through a slab is given by:
x=t⋅sini−sinrcosr
Where t is the thickness of the slab. We can express sini and sinr:
- sini=sin(π4)=√22
- sinr=sin(π6)=12
- cosr=cos(π6)=√32
x=t⋅√22−12√32=t⋅√2−12√32=t⋅√2−1√3
The maximum lateral displacement occurs when the angle of incidence is such that the light ray is incident normally (i.e., i=90∘). In this case, the maximum lateral displacement xmax can be calculated as:
xmax=t⋅sinicosr
Since sin(90∘)=1:
xmax=t⋅1cosr=t⋅1√32=2t√3
Now we find the ratio:
Ratio=xxmax=t⋅√2−1√32t√3
Cancelling t and √3:
Ratio=√2−12
The ratio of the lateral displacement suffered by the light ray to the maximum value which it could have suffered is:
√2−12
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE II LEVEL -II (ADVANCED) MORE THAN ONE CORRECT TYPE QUESTIONS)
7 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE II LEVEL -II (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)
9 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE II LEVEL -I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)
17 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
106 Videos
Similar Questions
Light ray is incident on a prism of angle A=60∘ are refractive index μ=√2. The angle of incidence which the emergent rays grazes the surface is given
View SolutionA light ray is incident on a glass sphere of reflective index μ=√3 at an angle of incidence 60∘ as shown in Fig. Find the angles r, r′ e and the total deviation after two refractions.
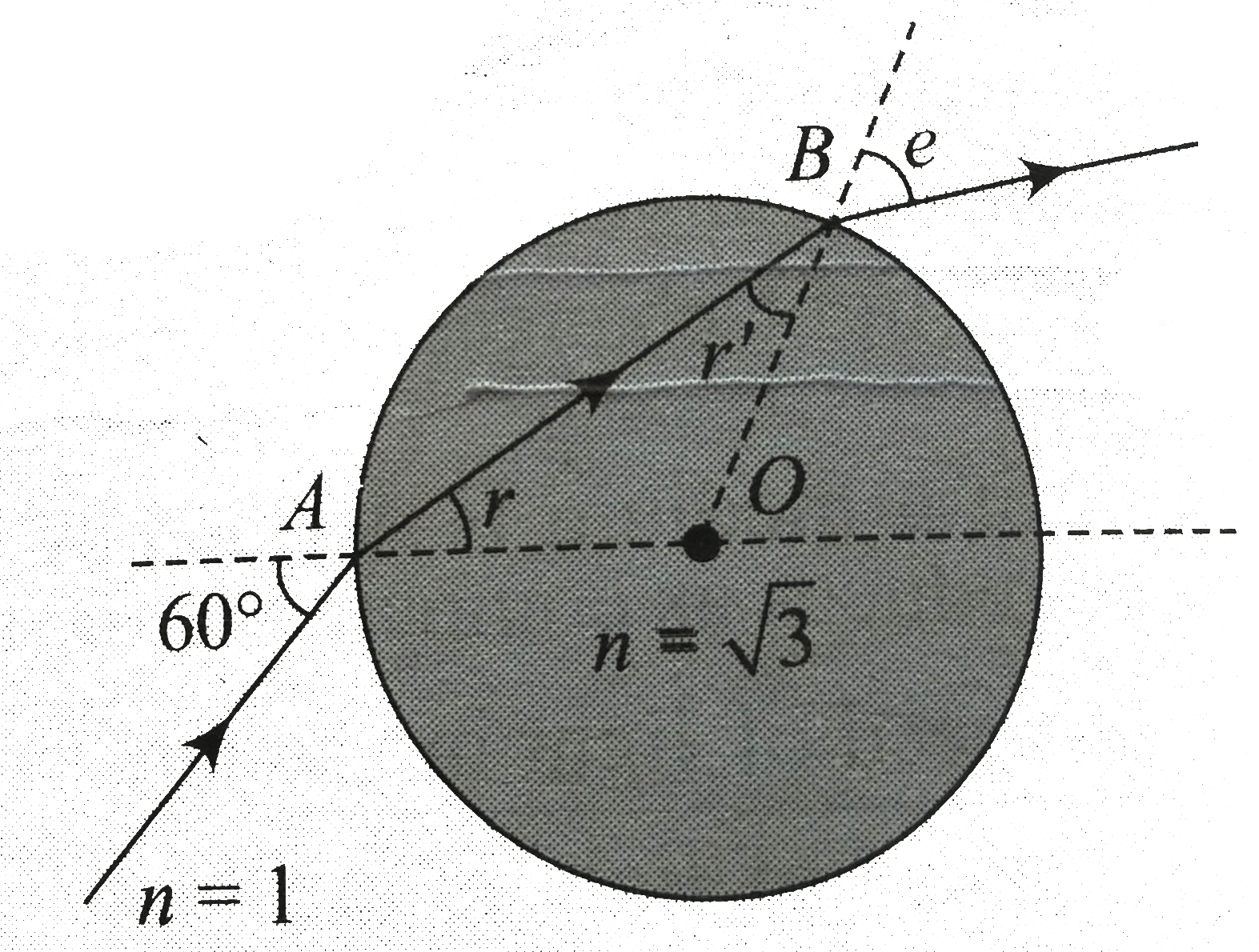
View Solution
Knowledge Check
A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45∘. The angle betweent the reflected and refracted rays is
A75∘B90∘C105∘D120∘
A ray of light is incident on a parallel slab of thickness t and refractive index n. If the angle of incidence θ is small, than the lateral displacement in the incident and emergent ray will be
View SolutionA ray of light is incident on the surface of a glass plate of refractive index √3 at the polarising angle . The angle of incidence and angle of refraction of the ray is
View SolutionA light ray is incident on a transparent sphere of index = √2 , at an angle of incidence =45∘ , What is the deviation of a tiny fraction of the ray, which enters the sphere, undergoes two internal reflections and then refracts out into air?
View Solution
A ray is incident on a sphere of refractive index √2 as shown in figure. Angle of refraction of the ray inside sphere is 30∘ if total deviation suffered by the ray is 30x0, then find x.
View SolutionA light ray is normally incident onone face of equilateral glass prism of refractive index √2. The deviation of light ray is
View SolutionA ray of light suffers a minimum deviation when incident on equilateral prism of refractive index √2 The angle of deviation is
View SolutionA ray of light is incident on one face of a transparent slab of thickness 15 cm. The angle of incidence is 60∘. If the lateral displacement of the ray on emerging from the parallel plane is 5√3 cm, the refractive index of the material of the slab is
View Solution
