A load of mass m falls from a height h on to the scale pan hung from a spring as shown in the adjoining figure. If the spring constant is k and mass of the scale pan is zero and the mass m does not bounce relative to the pan, then the amplitude of vibration is
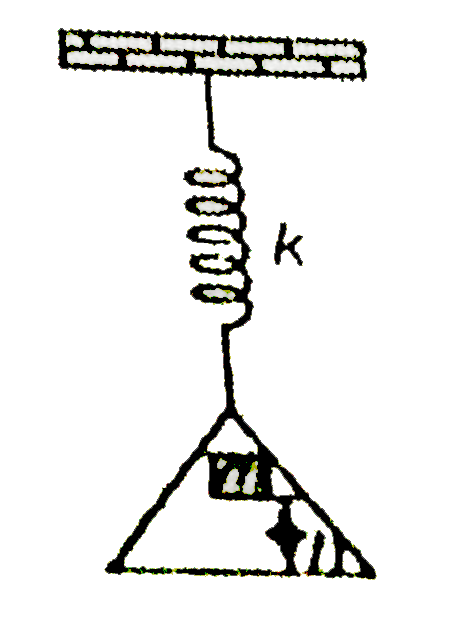
mgk
mgk√(1+2hkmg)
mgk+mgk√(1+2hkmg)
mgk√(1+2hkmg−mgk)
The correct Answer is:B
According to conservation principle
mgh=12kx20−mgx0
where, x0 is maximum elongation in spring (when particle is in its lowest extreme position).
or 12kx20−mgx0−mgh=0
or x20−2mgkx0−2mgkh=0
∴ x0=2mgk±√[(2mgk)2+4×2mgkh]2
∵ Amplitude=elongation in spring for lowest extreme position-elongation in spring for equilibrium position
=x0−x1=mgk√(1+2hkmg)
Topper's Solved these Questions
Similar Questions
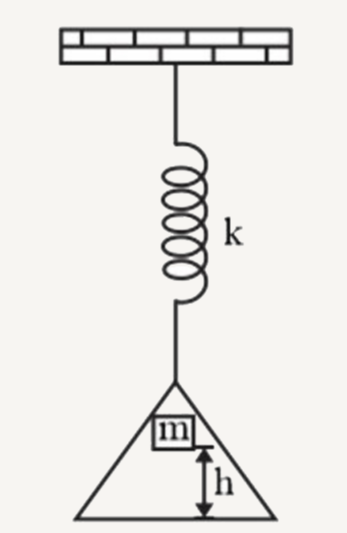
A load of mass m falls from a height h on to the scale pan hung from a spring , as shown in the figure . If the spring constant is k , mass of the not bounce , relative to the pan , then the amplitude of vibration is
 View Solution
View SolutionA body of mass m is released from a height h to a scale pan hung from a spring. The spring constant of the spring is k, the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
View Solution
Knowledge Check
- Question 1 - Select One
A load of mass m falls from a height h on to the scale pan hung from a spring , as shown in the figure . If the spring constant is k , mass of the not bounce , relative to the pan , then the amplitude of vibration is
 Amg/dBmgk√(1+2hkmg)Cmgk+mgk√(1+2hkmg)Dmgk√(1+2hkMg−mgk)
Amg/dBmgk√(1+2hkmg)Cmgk+mgk√(1+2hkmg)Dmgk√(1+2hkMg−mgk) - Question 2 - Select One
A body of mass m falls from a height h onto the pan of a spring balance. The masses of the pan and spring are negligible. The force constant of the spring is k. The body sticks to the pan and oscillates simple harmonically. The amplitude of oscillation is
 AmgkBmgk√1+2hkmgCmgk+mgk√1+2hkmgDNone of these
AmgkBmgk√1+2hkmgCmgk+mgk√1+2hkmgDNone of these - Question 3 - Select One
A body of mass m is released from a height h to a scale pan hung from a spring. The spring constant of the spring is k, the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
Amgk√1−2hkmgBmgkCmgk+mgk√1+2hkmgDmgk−mgk√1−2hkmg
A body of mass m is released from a height h to a scale pan hung from a spring. The spring constant of the spring is k, the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
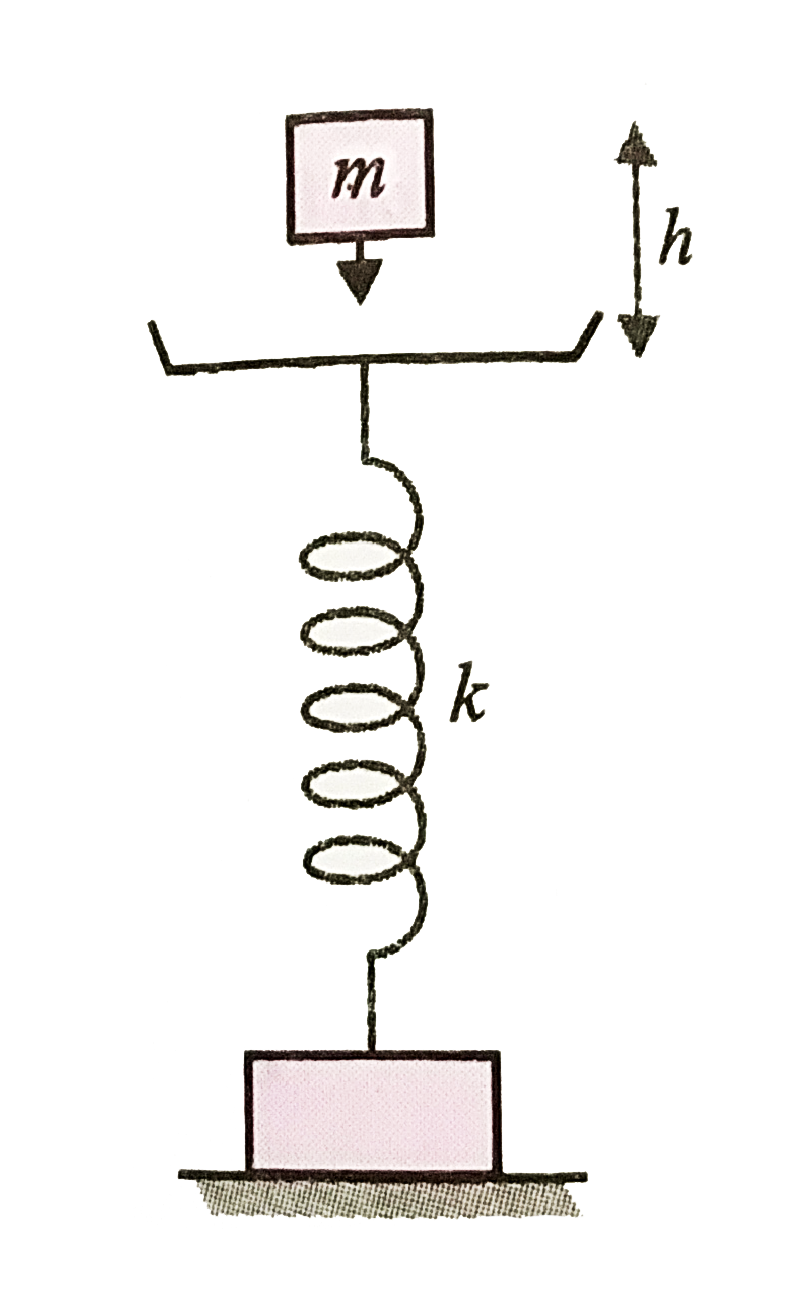
View SolutionA body of mass m falls from a height h on to the pan of a spring balance, figure, The masses of the pan and spring are negligible. The spring constant of the spring is k. The body gets attached to the pan and starts executing S.H.M. in the vertical direction. Find the amplitude and energy of oscillation.
 View Solution
View SolutionA body of mass m falls from a height h on to the pan of a spring balance. The masses of the pan and spring are negligible. The spring constant of the spring is k. Having stuck to the pan the body starts performing harmonic oscillations in the vertical direction. Find the amplitude and energy of oscillation.
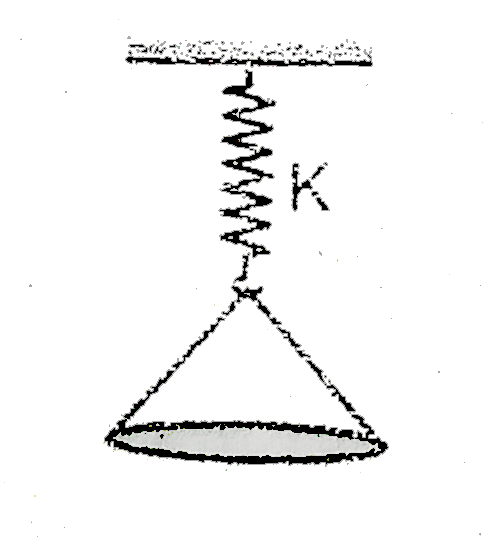
View SolutionA solid ball of mass m is made to fail from a height H on a pan suspended through a spring of spring constant K as shown in figure. If the does not rebound and the pan is massless, then amplitude of oscillation is
 View Solution
View SolutionA body of mass m falls from a height h onto the pan of a spring balance. The masses of the pan and spring are negligible. The force constant of the spring is k. The body sticks to the pan and oscillates simple harmonically. The amplitude of oscillation is
 View Solution
View Solution

