A long rectangular slab of transparent medium of thickness d placed on a table with its length parallel to the x-axis and width parallel to the axis. A ray of light travelling inair makes a near normal incidence on the slab as shown. Taking the point of incidence as orign (0,0,0). The refraction index μ of the medium varies as μ=μ01−(xr) where μ1 and r(>d) are constants. The refractive index of air is μ0
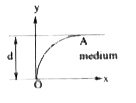
The x-coordinate of the point A where the ray intersects the upper surface of the slab air boundary is
−μ0√1−(dr)2
μ0√1−(dr)2
−μ0√1+(rd)2
μ0√1+(dr)2
The correct Answer is:B
Step by step video & image solution for A long rectangular slab of transparent medium of thickness d placed on a table with its length parallel to the x-axis and width parallel to the axis. A ray of light travelling inair makes a near normal incidence on the slab as shown. Taking the point of incidence as orign (0,0,0). The refraction index mu of the medium varies as mu=(mu_(0))/(1-(x/r) where mu_(1) and r(gtd) are constants. The refractive index of air is mu_(0) The x-coordinate of the point A where the ray intersects the upper surface of the slab air boundary is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE II LEVEL -II (ADVANCED) MATRIX MATCHING TYPE QUESTIONS)1videos
GEOMETRICAL OPTICS
- BOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE II LEVEL -II (ADVANCED) INTEGER TYPE QUESTIONS)2videos
GEOMETRICAL OPTICS
- BOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE II LEVEL -II (ADVANCED) MORE THAN ONE CORRECT TYPE QUESTIONS)7videos
GEOMETRICAL OPTICS
- BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS10videos
ELEMENTS OF VECTORS
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE106videos
LAWS OF MOTION
Similar Questions
For total internal reflection to take place, the angle of incidence i and the refractive index μ of the medium must satisfy the inequality
View SolutionA light ray enters from medium A to medium B as shown in the figure. The refractive index of medium B relative to A will be
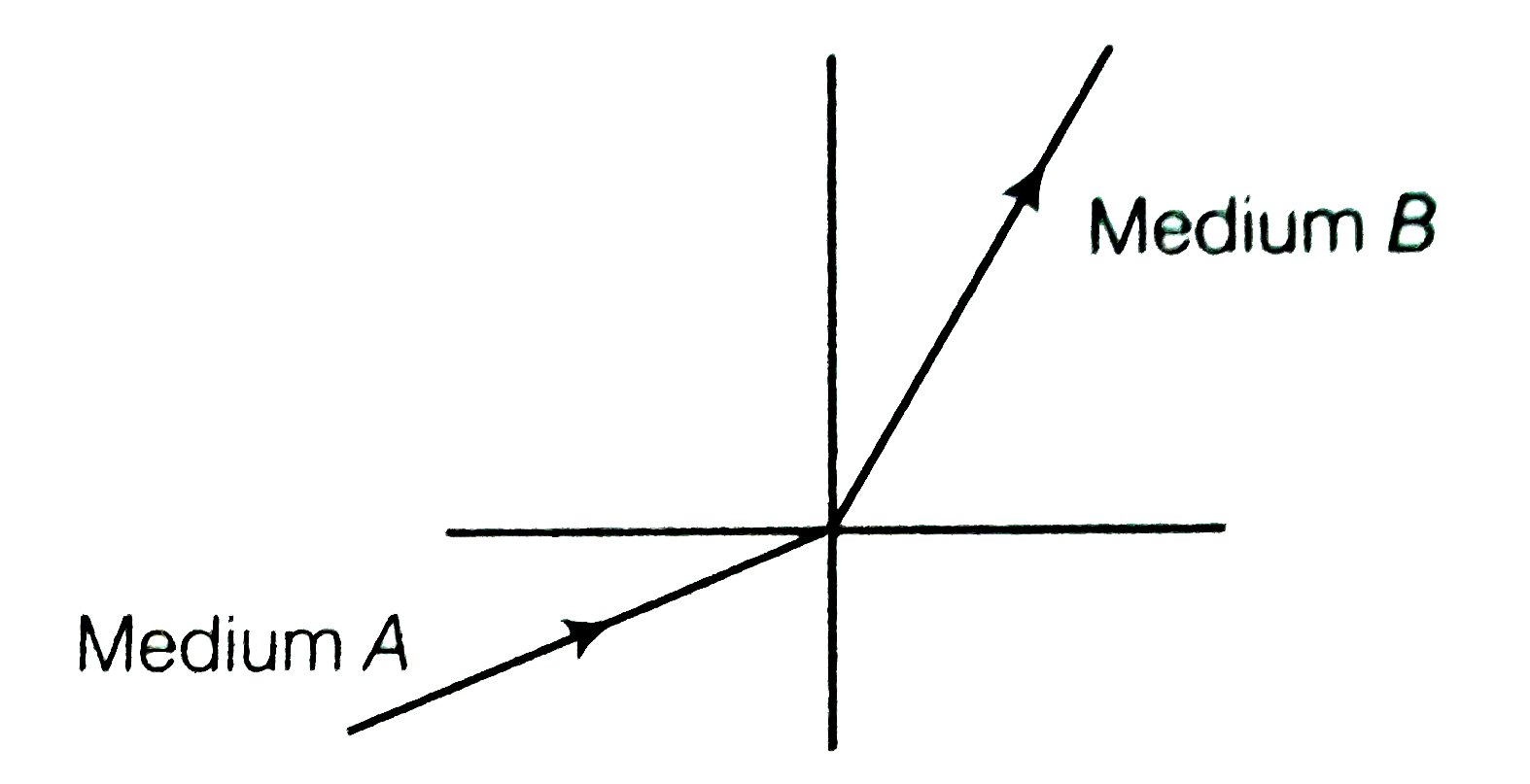 View Solution
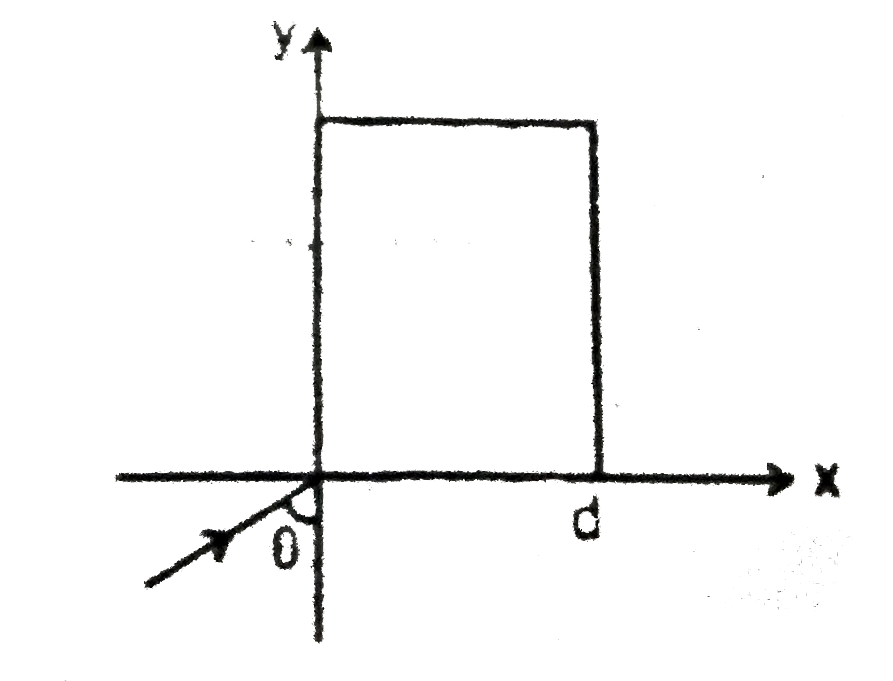
View SolutionA ray hits the y-axis making an angle θ with y-axis as shown in the figure. The variation of refractive index with x-coordinate is μ=μ0(1−xd) for 0≤x≤d(1−1μ0) and μ=μ0 for x<0, where d is a positive constant. The maximum x-coordinate of the path traced by the ray is
 View Solution
View SolutionFind the angle of deviation suffered by the light ray shown in figure. The refractive index μ=2.0 for the prism material.
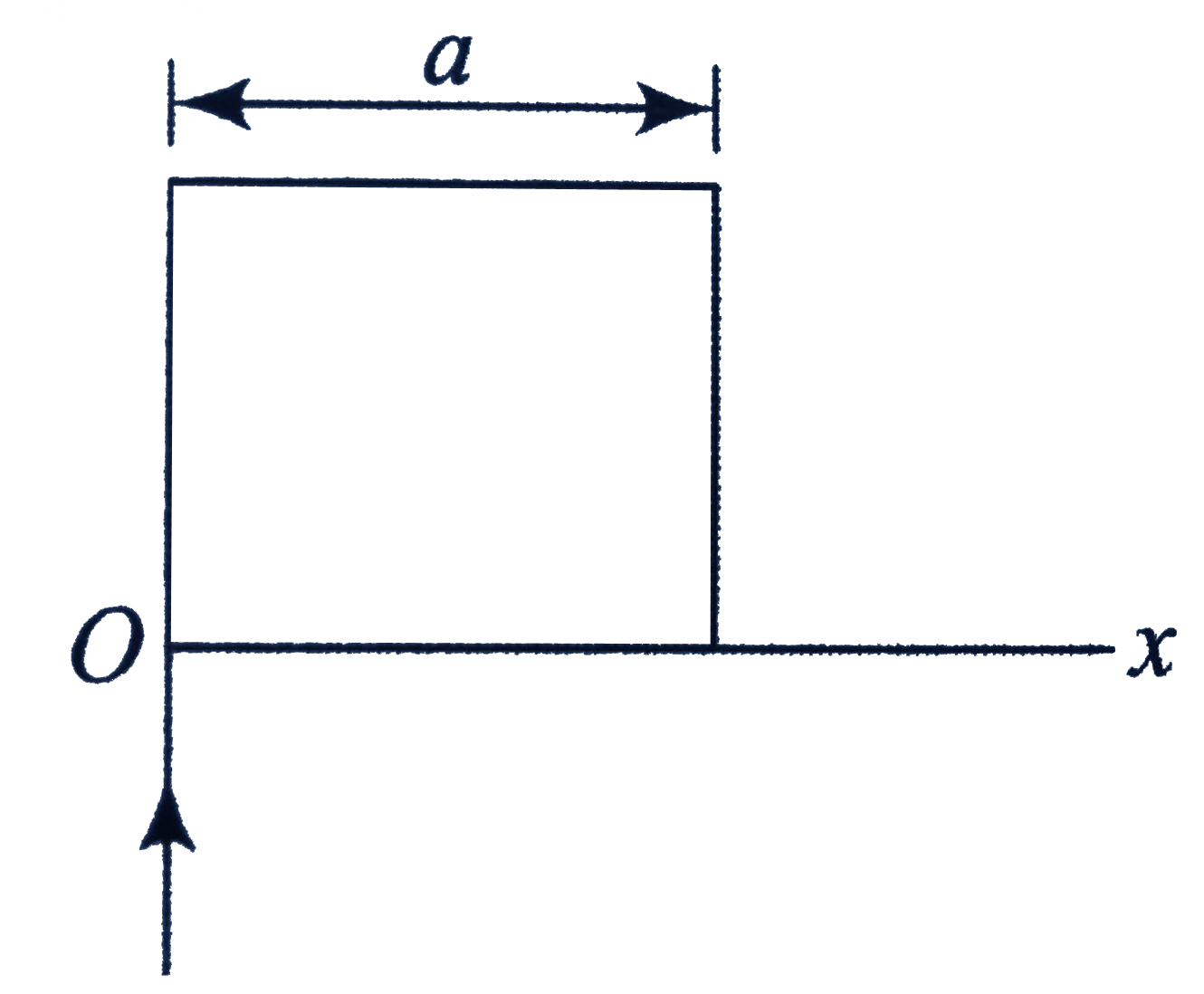
View SolutionThe refractive index of an anisotropic medium varies as μ=μ0√(x+1) , where 0≤x≤a. A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium .
 View Solution
View SolutionA ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by μ=√(1+y) . If the thickness of the slab is d=2m, determing the equation of the trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
View SolutionA parallel incident beam falls on a solid glass sphere at near normal incidence.Show that the image in terms of the index of refractive μ and the sphere of radius R is given by
R(2−μ)2(μ−1)View SolutionLight is incident on the thin lens as shown in figure. The refractive index of the material of the lens is μ2. The radii of curvature of both the surfaces are R. The refractive index of the medium of left side is μ1, while that of right side is μ3. What is the focal length of the lens?
 View Solution
View SolutionIf ε0 and μ0 are respectively the electric permittivity and the magnetic permeability of free space and ε and μ the corresponding quantities in a medium, the refractive index of the medium is
View SolutionA ray of light, travelling in a medium of refractive index 'mu_, is incident at an angle i on a composite transparent plate consisting of three plates of refractive indices μ1,μ2andμ3. The ray emerges from the composite plate into a medium of refractive index μ4, at angle x. Then,
View Solution
