A man of height 1.47 m stands on a straight road on a hot day. The vertical temperature in the air results in a variation of refractive index with height y as μ=μ0√(1+ay) where μ0 is the refractive index of air near the road a =1.5×10−6/m. What is the apparent length of the road man is able to sec?
700m
2000 m
7000√2
infinite distance
The correct Answer is:B
To solve the problem, we need to determine the apparent length of the road that the man can see, given the variation of the refractive index with height. Let's break down the solution step by step.
Step 1: Understand the refractive index variation
The refractive index μ varies with height y as:
μ=μ0√1+ay
where μ0 is the refractive index of air near the road, and a=1.5×10−6m−1.
Step 2: Determine the height of the man
The height of the man is given as h=1.47m.
Step 3: Use the small angle approximation
For small angles, the apparent distance x that the man can see can be related to the height h and the refractive index. The relationship can be derived from the geometry of the situation and the behavior of light in a medium with varying refractive index.
Step 4: Set up the relationship
Using the formula for the apparent distance:
dydx=√μ2−sin2θμsinθ
where μ=μ0√1+ay.
Step 5: Substitute the values
We can simplify this to find dx in terms of dy:
dydx=√μ20(1+ay)−sin2θ÷(μ0sinθ)
Step 6: Integrate to find the total distance
We integrate from y=0 to y=h (1.47 m) to find the total distance x:
x=∫h0dy√μ20(1+ay)−sin2θ
Step 7: Solve for the apparent length
After performing the integration and substituting the values, we find:
x=2√h√μ0a
Step 8: Substitute known values
Assuming μ0≈1 (the refractive index of air), we have:
x=2√1.47√1⋅1.5×10−6
Calculating this gives:
x≈1979m
Step 9: Final result
Thus, the apparent length of the road that the man can see is approximately 2000m.
The refractive index μ varies with height y as:
μ=μ0√1+ay
where μ0 is the refractive index of air near the road, and a=1.5×10−6m−1.
The height of the man is given as h=1.47m.
For small angles, the apparent distance x that the man can see can be related to the height h and the refractive index. The relationship can be derived from the geometry of the situation and the behavior of light in a medium with varying refractive index.
Using the formula for the apparent distance:
dydx=√μ2−sin2θμsinθ
where μ=μ0√1+ay.
We can simplify this to find dx in terms of dy:
dydx=√μ20(1+ay)−sin2θ÷(μ0sinθ)
We integrate from y=0 to y=h (1.47 m) to find the total distance x:
x=∫h0dy√μ20(1+ay)−sin2θ
After performing the integration and substituting the values, we find:
x=2√h√μ0a
Assuming μ0≈1 (the refractive index of air), we have:
x=2√1.47√1⋅1.5×10−6
x≈1979m
Thus, the apparent length of the road that the man can see is approximately 2000m.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE II LEVEL -II (ADVANCED) MORE THAN ONE CORRECT TYPE QUESTIONS)
7 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE II LEVEL -II (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)
9 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE II LEVEL -I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)
17 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
106 Videos
Similar Questions
A man of height 1.47 m stands on a straight road on a hot day. The vertical temperature in the air results in a variation of refractive index with height y as μ=μ0√(1+ay) where μ0 is the refractive index of air near the road a =1.5×10−6/m. What is the apparent length of the road man is able to sec?
View SolutionA man of height 2 m stands on a straight road on a hot day. The vertical temperature in the air results in a variation of refractive index with height y as μ=μ0√(1+ay) where μ0 is the refractive index of air near the road and a=2×10−6/m. What is the actual length of the road, man is able to see
View SolutionWhat is the refractive index in a medium where the speed of light is 1.5×108 m/s ?
View SolutionA man of height 2.0m is standing on a level road because of temprature variation the refractive index of air is varying as μ=√1+ay, where y is height from road. If a=2.0×10−6m−1. Then, find distant point that he can see on the road.
View SolutionDue to a vertical temperature gradient in the atmosphere, the index of refraction varies. Suppose index of refraction varies as n=n0√1+ay, where n0 is the index of refraction at the surface and a=2.0×10−6m−1 . A person of height h=2.0m stands on a level surface. Beyond what distance will he not see the runway?

View SolutionA long rectangular slab of transparent medium of thickness d placed on a table with its length parallel to the x-axis and width parallel to the axis. A ray of light travelling inair makes a near normal incidence on the slab as shown. Taking the point of incidence as orign (0,0,0). The refraction index μ of the medium varies as μ=μ01−(xr) where μ1 and r(>d) are constants. The refractive index of air is μ0
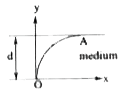
The x-coordinate of the point A where the ray intersects the upper surface of the slab air boundary is
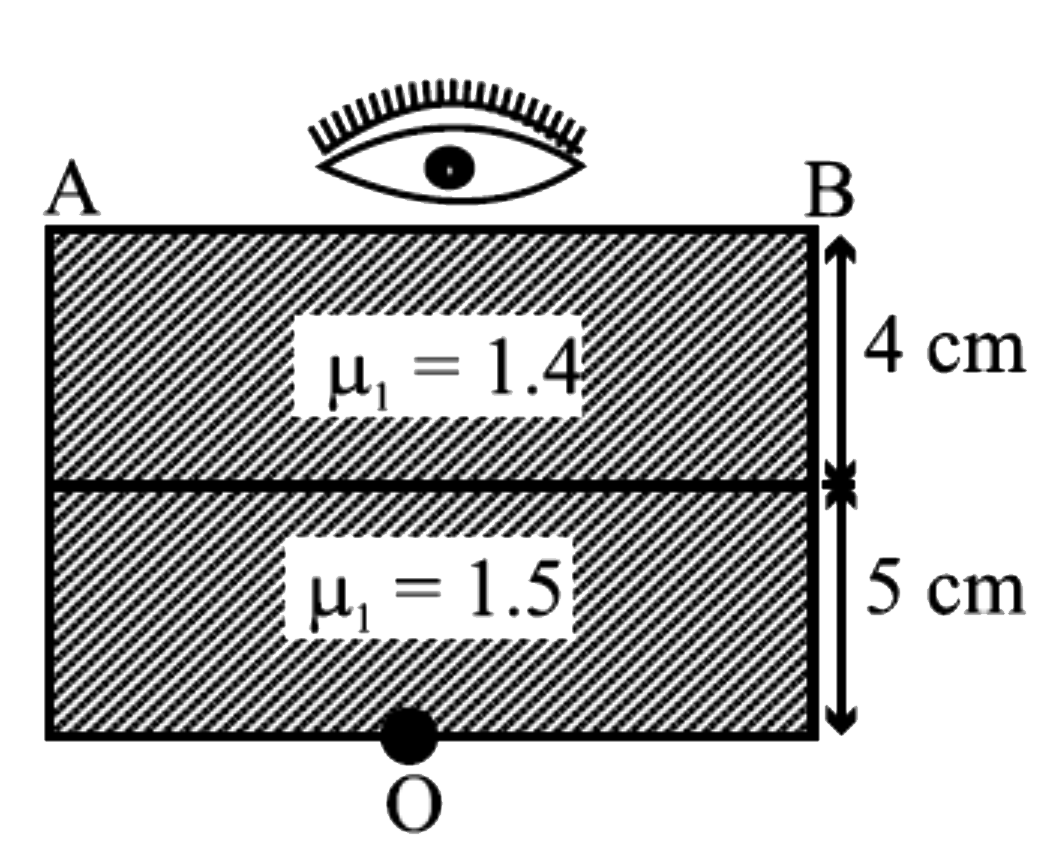
View SolutionThe apparent depth of an object O from AB is
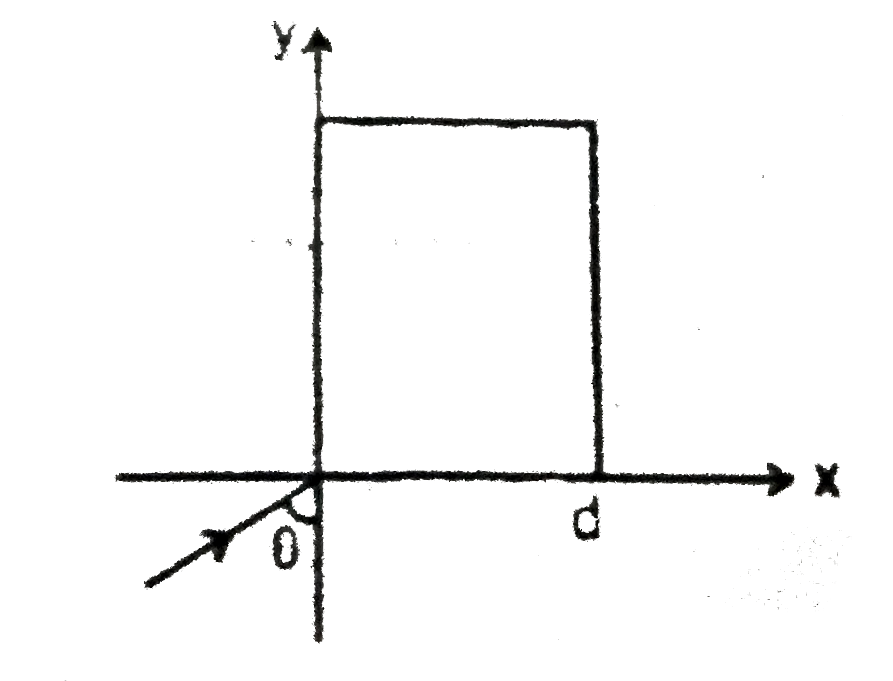
View SolutionA ray hits the y-axis making an angle θ with y-axis as shown in the figure. The variation of refractive index with x-coordinate is μ=μ0(1−xd) for 0≤x≤d(1−1μ0) and μ=μ0 for x<0, where d is a positive constant. The maximum x-coordinate of the path traced by the ray is
View SolutionThe figure shows a transparent slab of length m placed in air whose refractive index in x direction varies as μ=1+x2(0<x<1). The optical path length of ray R will be

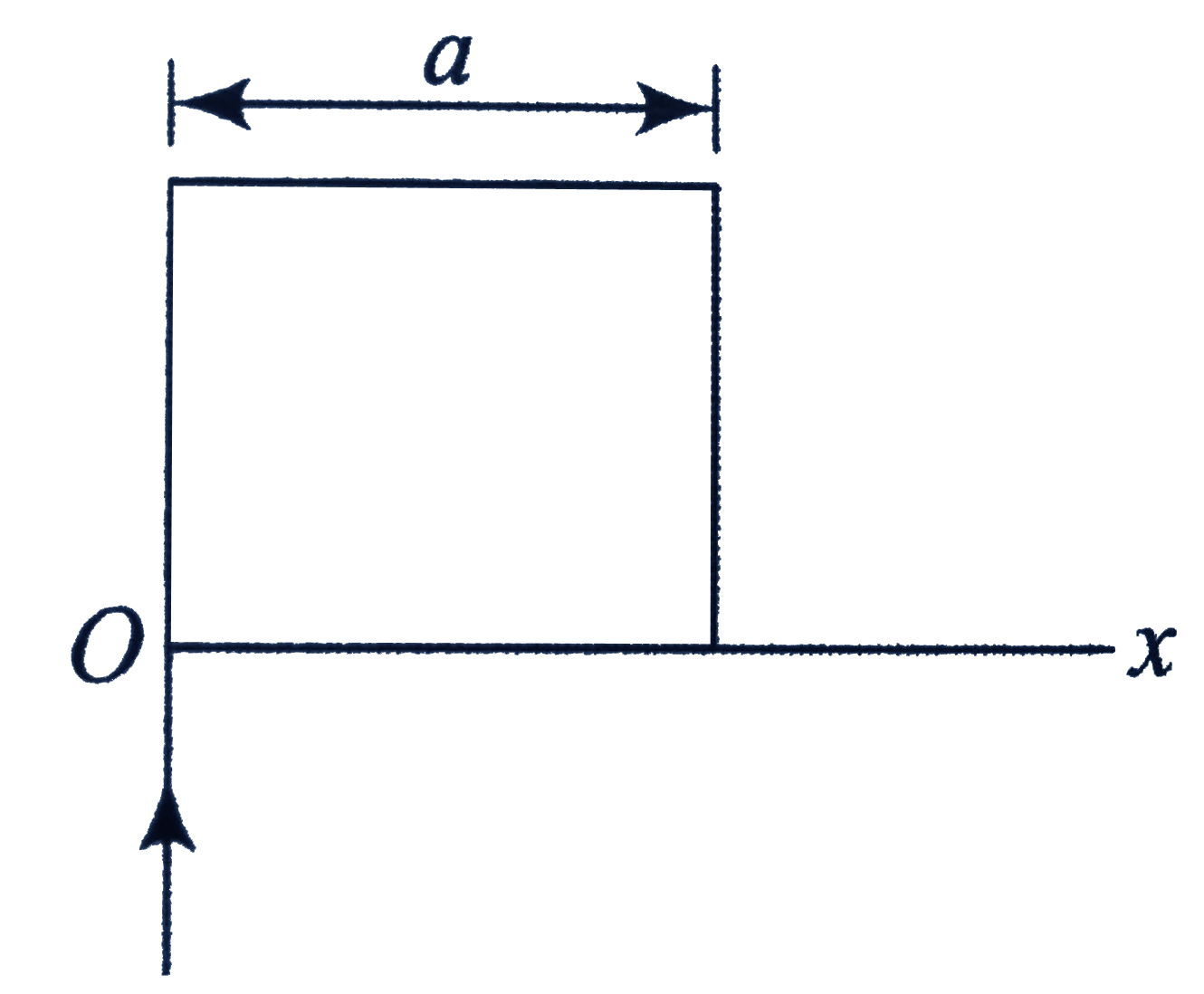
View SolutionThe refractive index of an anisotropic medium varies as μ=μ0√(x+1) , where 0≤x≤a. A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium .
View Solution
