A man of height 1.47 m stands on a straight road on a hot day. The ver

A man of height 1.47 m stands on a straight road on a hot day. The vertical temperature in the air results in a variation of refractive index with height y as $μ = μ_{0} \sqrt{(1 + a y)}$ where $μ_{0}$ is the refractive index of air near the road a $= 1.5 \times 10^{- 6}$ /m. What is the apparent length of the road man is able to sec?

View Solution

A man of height 2 m stands on a straight road on a hot day. The vertical temperature in the air results in a variation of refractive index with height y as $μ = μ_{0} \sqrt{(1 + a y)}$ where $μ_{0}$ is the refractive index of air near the road and a= $2 \times 10^{- 6} / m$ . What is the actual length of the road, man is able to see

View Solution

What is the refractive index in a medium where the speed of light is $1.5 \times 10^{8}$ m/s ?

View Solution

A man of height $2.0 m$ is standing on a level road because of temprature variation the refractive index of air is varying as $μ = \sqrt{1 + a y},$ where y is height from road. If $a = 2.0 \times 10^{- 6} m^{- 1} .$ Then, find distant point that he can see on the road.

View Solution

Due to a vertical temperature gradient in the atmosphere, the index of refraction varies. Suppose index of refraction varies as $n = n_{0}$ $\sqrt{1 + a y}$ , where $n_{0}$ is the index of refraction at the surface and $a = 2.0 \times 10^{- 6} m^{- 1}$ . A person of height $h = 2.0 m$ stands on a level surface. Beyond what distance will he not see the runway?
ocr_image

View Solution

A long rectangular slab of transparent medium of thickness d placed on a table with its length parallel to the x-axis and width parallel to the axis. A ray of light travelling inair makes a near normal incidence on the slab as shown. Taking the point of incidence as orign (0,0,0). The refraction index $μ$ of the medium varies as $μ = \frac{μ_{0}}{1 - (\frac{x}{r})}$ where $μ_{1}$ and $r (> d)$ are constants. The refractive index of air is $μ_{0}$
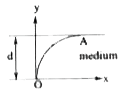
ocr_image
The x-coordinate of the point A where the ray intersects the upper surface of the slab air boundary is

View Solution

The apparent depth of an object O from AB is
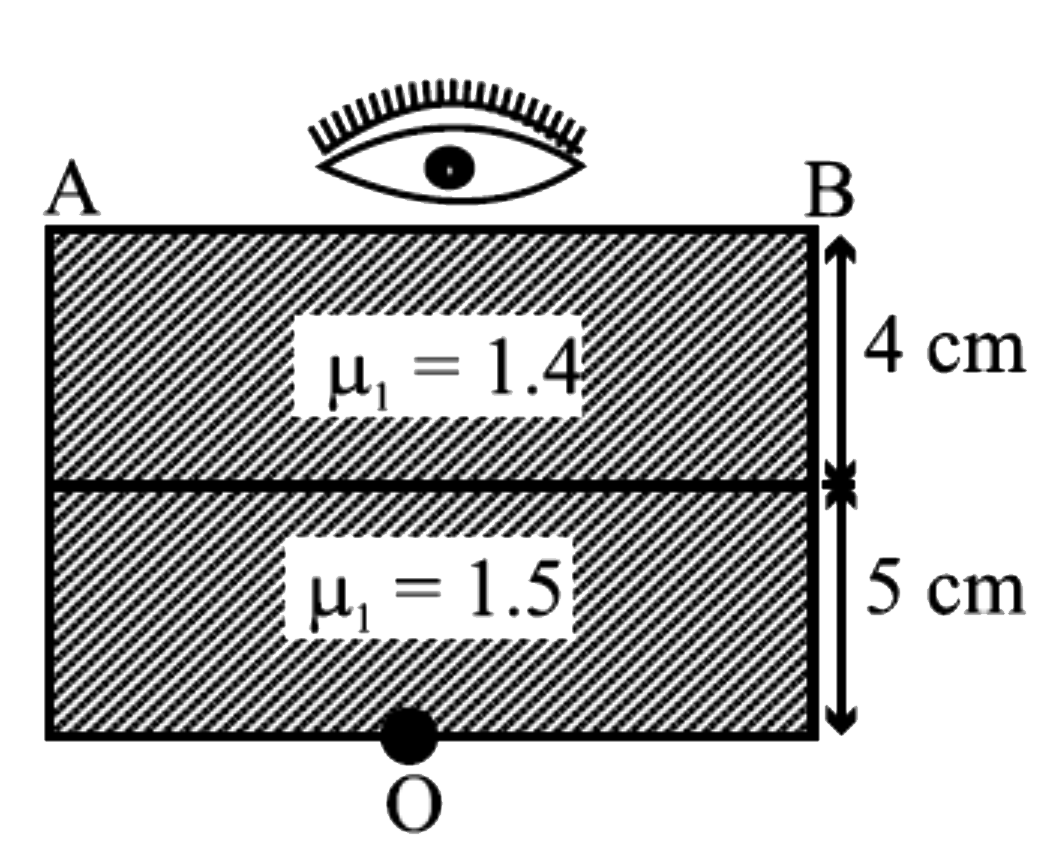ocr_image

View Solution

A ray hits the y-axis making an angle $θ$ with y-axis as shown in the figure. The variation of refractive index with x-coordinate is $μ = μ_{0} (1 - \frac{x}{d})$ for $0 \leq x \leq d (1 - \frac{1}{μ_{0}})$ and $μ = μ_{0}$ for $x < 0$ , where d is a positive constant. The maximum x-coordinate of the path traced by the ray is
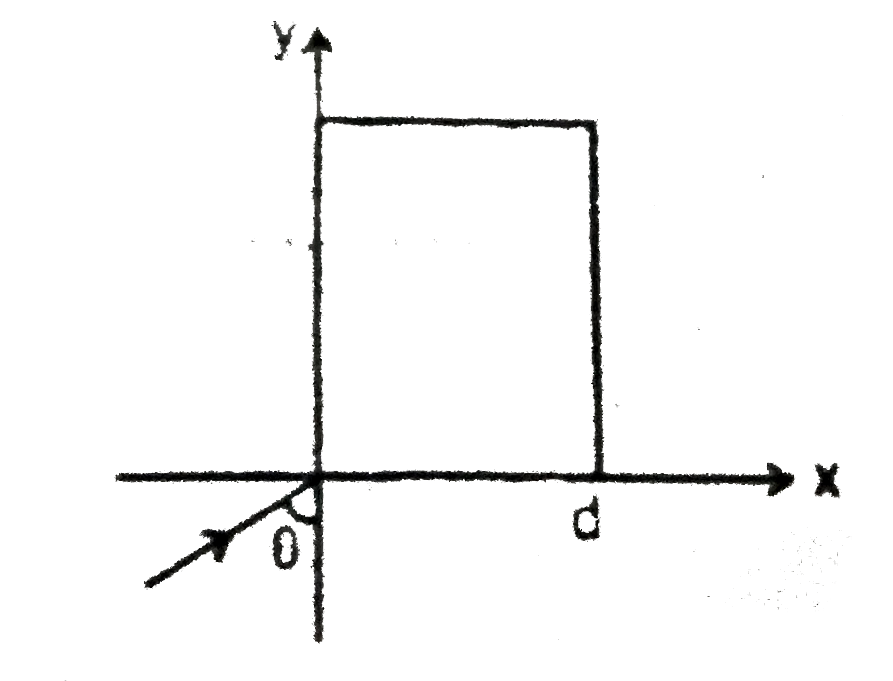ocr_image

View Solution

The figure shows a transparent slab of length m placed in air whose refractive index in x direction varies as $μ = 1 + x^{2} (0 < x < 1)$ . The optical path length of ray R will be
ocr_image

View Solution

The refractive index of an anisotropic medium varies as $μ = μ_{0} \sqrt{(x + 1)}$ , where $0 \leq x \leq a$ . A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium .
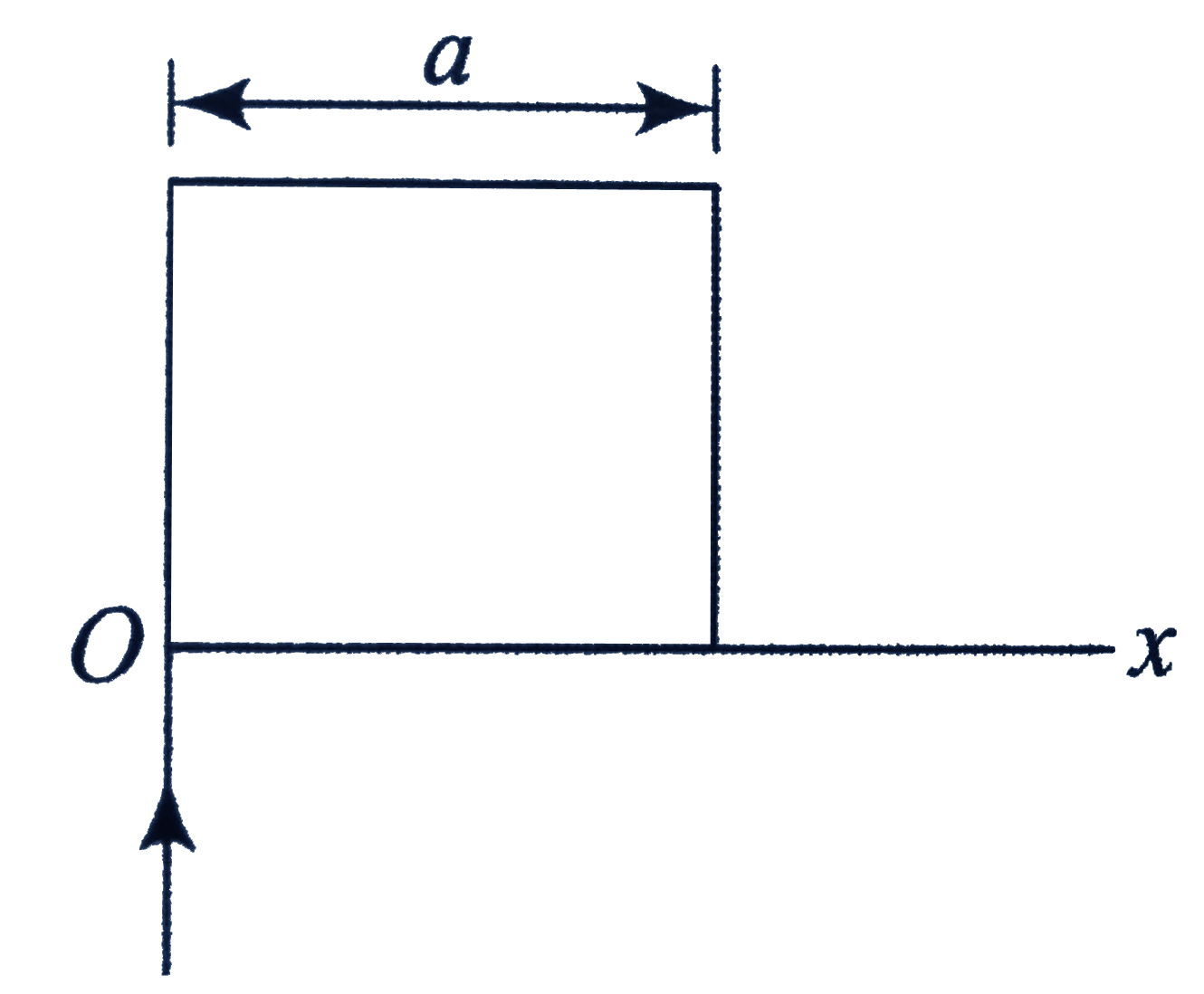ocr_image

View Solution

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

AAKASH SERIES-GEOMETRICAL OPTICS-LECTURE SHEET (EXERCISE-II (LEVEL-II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS))