A man wants to reach point B on the opposite bank of a river flowing at a speed u as shown in (Fig. 5.193). What minimum speed relative to water to water should the man have so that he can reach directly to point B ? In which direction should he swim ?
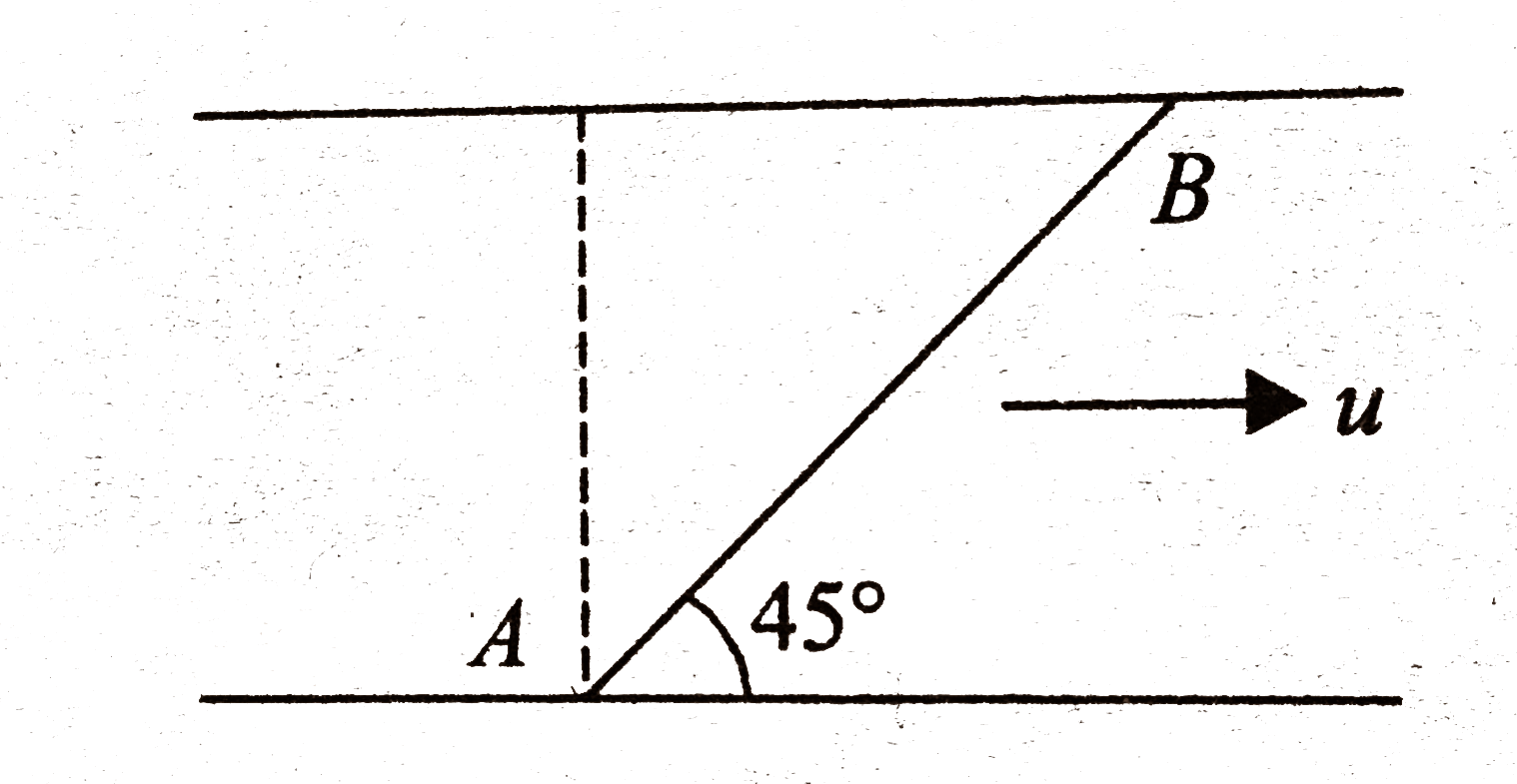 .
.
u,45∘ North-West
u,45∘ North-East
u√2,45∘ North-West
u√2,45∘ North-East
The correct Answer is:C
Let υ be the speed boatman in still water. Resultant of υ and u should be along AB. Components of vb (absolute velocity of boatman) along x and y directions are,
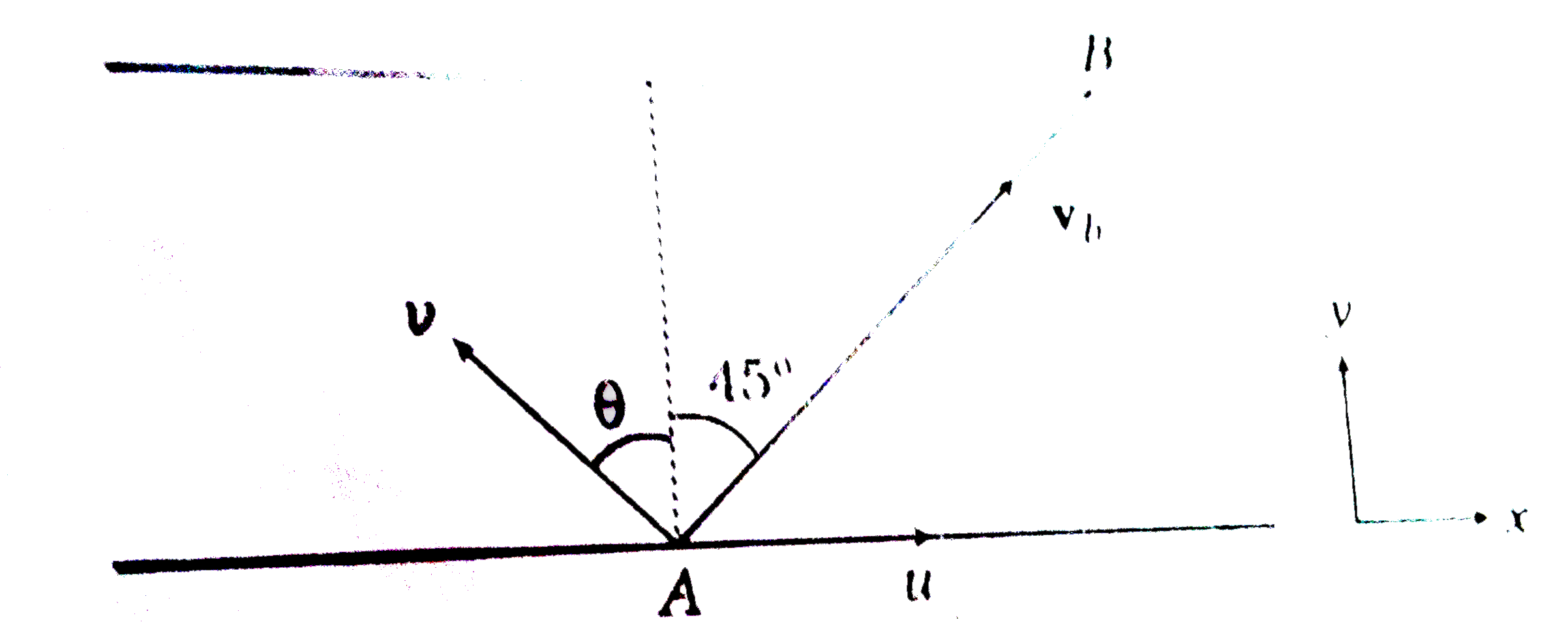
υx=u−υsinθ and υy=υcosθ
Further, tan45∘=υyυx or 1=υcosθu−υsinθ
∴υ=usinθ+coshη=u√2sin(θ+45∘)
υ is minimum at,
θ+45∘=90∘ or θ=45∘ and υmin=u√2
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - (A) Taking it together
75 Videos
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Assertion and reason)
19 Videos
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.6
20 Videos
- MOTIONBOOK - DC PANDEYCHAPTER - MOTIONEXERCISE - Medical entrances gallery
19 Videos
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
Similar Questions
A man wants to reach point B on the opposite bank of a river flowing at a speed 4m/s as shown in the fig 1E.125 (a) what minimum speed relative to water should the man have so that he can reach point B directly by swimming? In which direction should he swin?
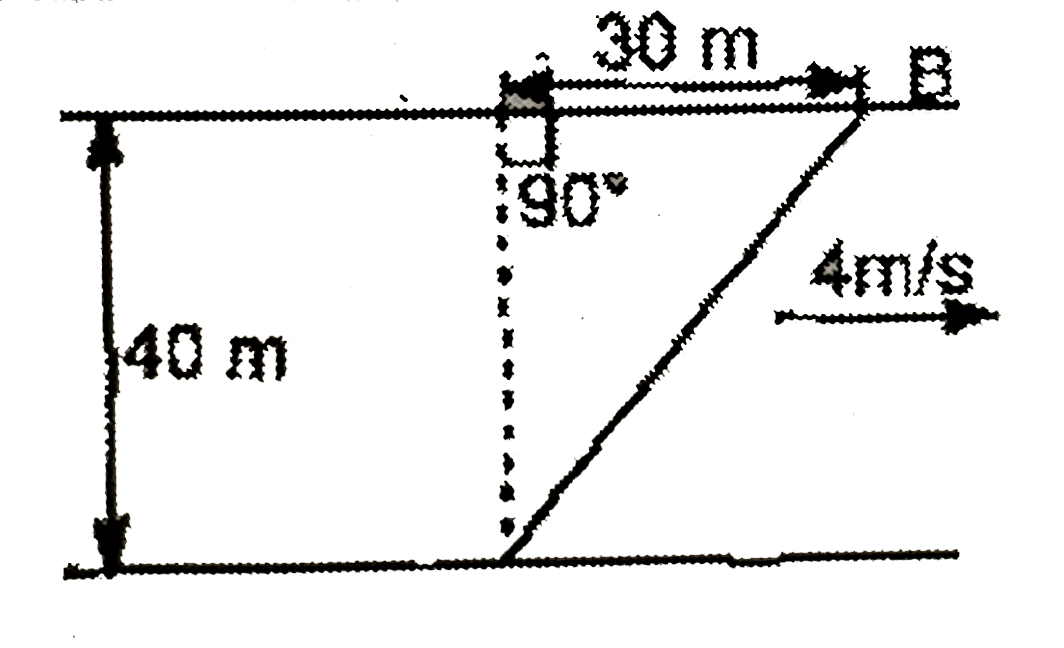
View SolutionA man wants to reach point B on the opposite bank of a river flowing at a speed as shown in figure. What minimum speed relative to water should the man have so that he can reach point B? In which direction should he swim?
View Solution
Knowledge Check
A man wants to reach point B on the opposite bank of a river flowing at a speed 4m/s as shown in the figure. What minimum speed relative to water should the man have so that he can reach point B directly by swimming?
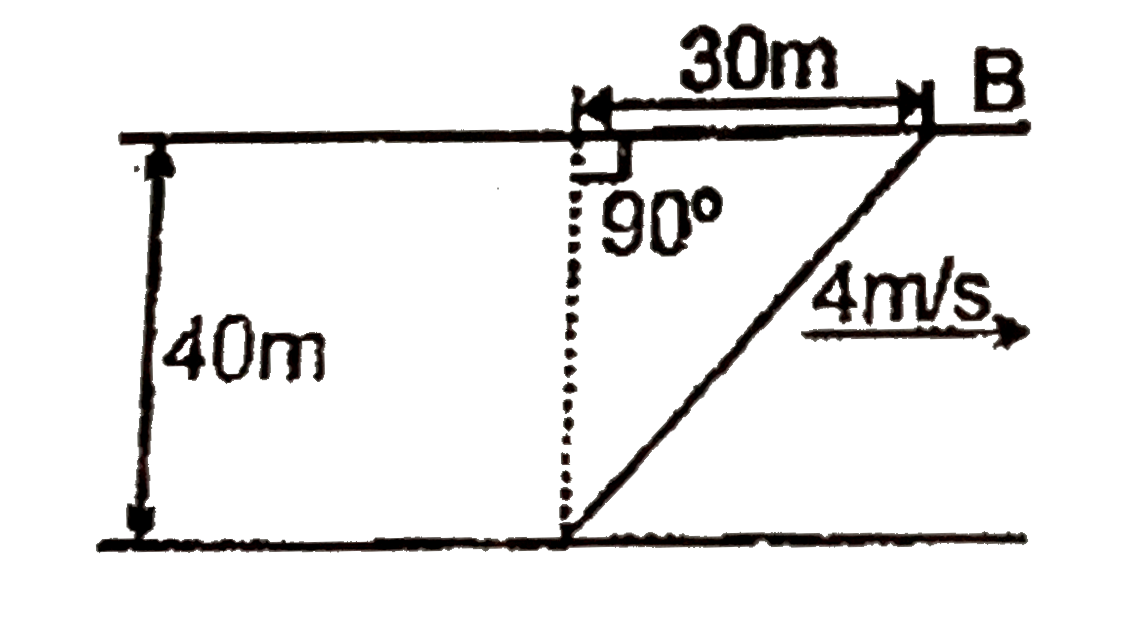 A8m/sB3.2m/sC6.5m/sD7√2m/s
A8m/sB3.2m/sC6.5m/sD7√2m/sA man in a row boat must get from point A to point B on the opposite bank of the river (see figure).The distance BC=a.The width of the river AC=b.At what minimum speed u relative to the still water should the boat travel to reach the point B?The velocity of flow of the river is v0
 Av0b√a2+b2Bv0a√a2+b2Cv0b√2aDv0a√2b
Av0b√a2+b2Bv0a√a2+b2Cv0b√2aDv0a√2bA man who can swim at a velocity v relative to water wants to cross a river of width b, flowing with a speed u.
AThe minimum time in which he can cross the river is bvBHe can reach a point exactly opposite on the bank in time t=b√v2−u2ifv>uCHe cannot reach a point exactly opposite on the bank if u>vDHe cannot reach a point exactly opposite on the bank if v>u
A swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as hown. The velocity of the swimmer in still water is same as that of the water

(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity anf river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.
View SolutionA swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as shown. The velocity of the swimmer in still water is same as that of the water
(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity ? Calculate angle between his velocity and river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.

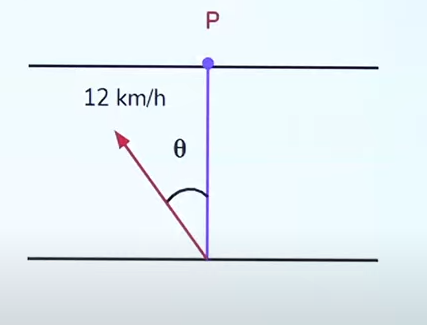
View SolutionA swimmer can swim with speed 12 m/s in still water. Speed of river is 6 m/s. Find angle at which he should swim with downstream so that he reaches directly opposite point on other side
View Solution(a) In which direction should the motorboat given in Illustration 5.46 head in order to reach a point on the opposite bank directly east from the starting point ? The boat's speed relative to the water remains 4ms−1.
(b) What is the velocity of the boat relative to the earth ?
( c) How much time is required to cross the river ?
View SolutionA man swims from a point A on the bank of a river if width 100m. When he swims perpendicular to the water current, he reaches the other bank 50m downstream. The angle to the bank at which he should swim, to reach the directly opposite point B on the other bank is.
 .
.
View Solution
