A mass attached to a string rotates about a fixed centre with an angular velocity ω in a horizontal plane ,The length of the string and the angular velocity are now doubled .IF T0 is the initial tension in the string , then the new tension will be
2T0
4T0
8T0
6T0
The correct Answer is:C
TT0=mr2ω22mr1ω21=8
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - MARVEL PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - TEST YOUR GRASP-1
1 Videos
- CIRCULAR MOTIONBOOK - MARVEL PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - TEST YOUR GRASP-2
1 Videos
- ATOMS, MOLECULES AND NUCLEI BOOK - MARVEL PUBLICATIONCHAPTER - ATOMS, MOLECULES AND NUCLEI EXERCISE - TEST YOUR GRASP
30 Videos
- COMMUNICATION SYSTEMS BOOK - MARVEL PUBLICATIONCHAPTER - COMMUNICATION SYSTEMS EXERCISE - TEST YOUR GRASP -20
10 Videos
Similar Questions
Knowledge Check
A mass is supported on a frictionless horizontal surface. It Is attached to a string and rotates about a fixed center at an angular velocity ω0.If the length of the string and angular velocity both are doubled, the tension in the string which was initially T0 is now
AT0BT0/2C4T0D8T0A stone is tied to one end of a steing and rotated in horizontal circle with a uniform angular velocity. The tension in the string is T, if the lrngth of the string is halved and its angular velocity is doubled , the tension in the string will be
A4 TBT/2CT/4D2 TA particle attached to a string is rotating with a constant angular velocity and its angular momentum is L. If the string is halved and angular velocity is kept constant, the angular momentum will be
AL/4BL/2CLD2L
A ring of mass m and radius R is being rotated about its axis with constant angular velocity ω in the gravity free space. Find tension in the ring.
View SolutionA mass is whirled in a circular path with an angular momentum L. If the length of string and angular velocity, both are doubled, the new angular momentum is
View SolutionA rod is rotating with angular velocity ω about axis AB. Find cosθ.

View SolutionA mass is whirled in a circular path with an angular momentum L. If the length of string is now halved keeping the angular velocity same, the new angular momentum is
View SolutionA uniform rod AB of length l rotating with an angular velocity ω while its centre moves with a linear velocity v=ωl6 If the end A of the rod is suddenly fixed, the angular velocity of
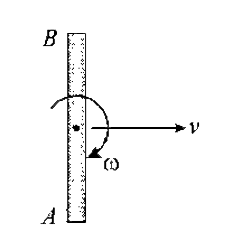
View Solution
