A mass of 6 kg is suspended by a rope of length 2 m from the ceilling A force of 50 N in the horizontal direction is applied at the mid - point P of the rope as shown . What is the angle the rope makes with the vertical in equilibrium ? (Take = 10ms−2) . Neglect mass of the rope .
To solve the problem, we will analyze the forces acting on the mass and the rope. Here's a step-by-step solution:
Step 1: Identify the Forces Acting on the Mass
The mass of 6 kg creates a gravitational force acting downward, which can be calculated as:
Fg=m⋅g
Where:
- m=6kg
- g=10m/s2
Calculating the gravitational force:
Fg=6kg⋅10m/s2=60N
Step 2: Draw the Free Body Diagram (FBD)
At point P (the midpoint of the rope), we have:
- A tension T1 acting along the rope on one side.
- A tension T2 acting along the rope on the other side.
- A horizontal force of 50 N acting at point P.
Step 3: Set Up the Equations of Equilibrium
In equilibrium, the sum of forces in both the horizontal and vertical directions must equal zero.
Vertical Forces:
The vertical component of the tension must balance the weight of the mass:
T2=60N
Horizontal Forces:
The horizontal component of the tension must balance the applied force:
T1sinθ=50N
Step 4: Relate the Tensions
The vertical component of the tension must balance the weight:
T1cosθ=T2=60N
Step 5: Solve for the Angles
Now we have two equations:
1. T1sinθ=50N (1)
2. T1cosθ=60N (2)
We can divide equation (1) by equation (2):
T1sinθT1cosθ=5060
This simplifies to:
tanθ=5060=56
Step 6: Calculate the Angle
To find the angle θ:
θ=tan−1(56)
Using a calculator:
θ≈40.6∘
Final Answer
The angle the rope makes with the vertical in equilibrium is approximately 40.6∘.
---
The mass of 6 kg creates a gravitational force acting downward, which can be calculated as:
Fg=m⋅g
Where:
- m=6kg
- g=10m/s2
Fg=6kg⋅10m/s2=60N
At point P (the midpoint of the rope), we have:
- A tension T1 acting along the rope on one side.
- A tension T2 acting along the rope on the other side.
- A horizontal force of 50 N acting at point P.
In equilibrium, the sum of forces in both the horizontal and vertical directions must equal zero.
The vertical component of the tension must balance the weight of the mass:
T2=60N
The horizontal component of the tension must balance the applied force:
T1sinθ=50N
The vertical component of the tension must balance the weight:
T1cosθ=T2=60N
Now we have two equations:
1. T1sinθ=50N (1)
2. T1cosθ=60N (2)
T1sinθT1cosθ=5060
This simplifies to:
tanθ=5060=56
To find the angle θ:
θ=tan−1(56)
θ≈40.6∘
The angle the rope makes with the vertical in equilibrium is approximately 40.6∘.
Topper's Solved these Questions
Similar Questions
See Fig 5.8 .A mass of 6 kg is suspended by a rope of length 2m from the ceiling . A force of 50 N in the horizontal direction is applied at the mid-point P of the rope, as shown. What is the angle the rope makes with the vertical in equilibrium ? (Take g = 10 m s−2). Neglect the mass of the rope.
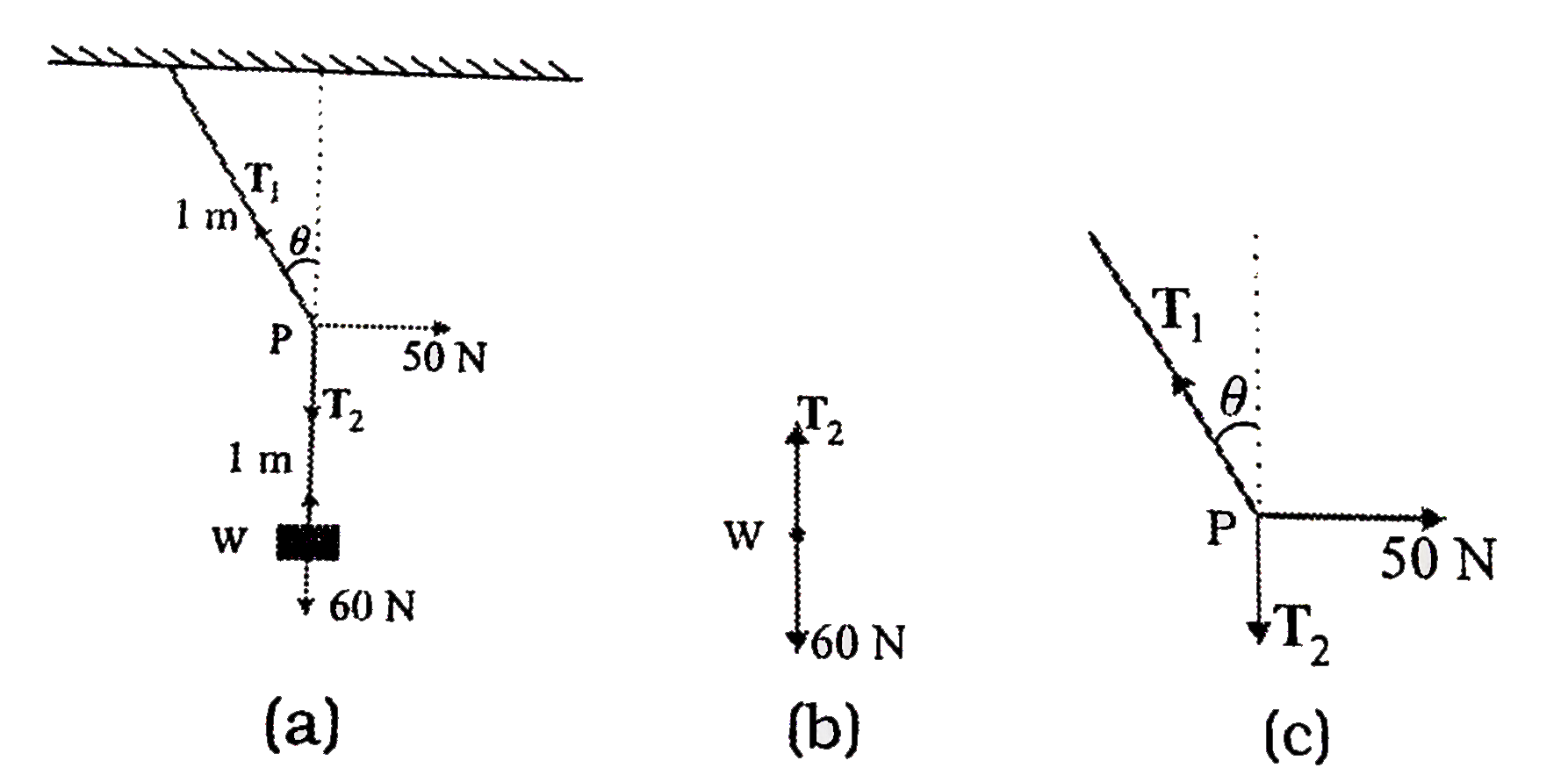
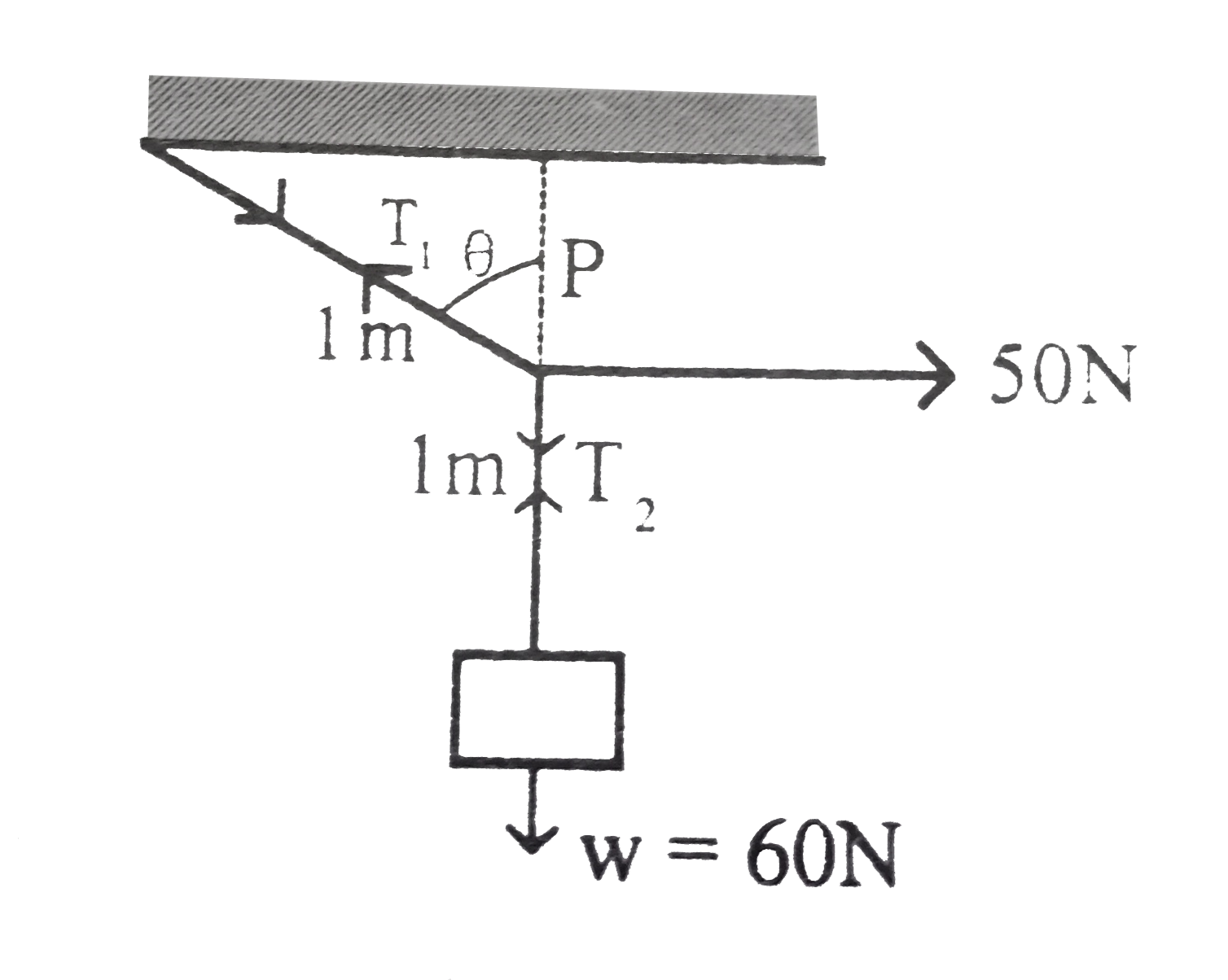
View SolutionA mass of 6 kg is suspended by a rope of length 2m from a celling. A force of 50N is applied in horizontal direction at the mid point of the rope. What is the angle of the rope with the verticle in equilibrium:-
View Solution
Knowledge Check
A block fof mass 5kg is suspended by a massless rope of length 2 m from the ceilling. A force of 50 N is applied in the horizontal direction at the midpoint P of the rope, as shown in the figure. The angle made by the rope with the vertical in equilibrium is (Take g=10ms−2m .
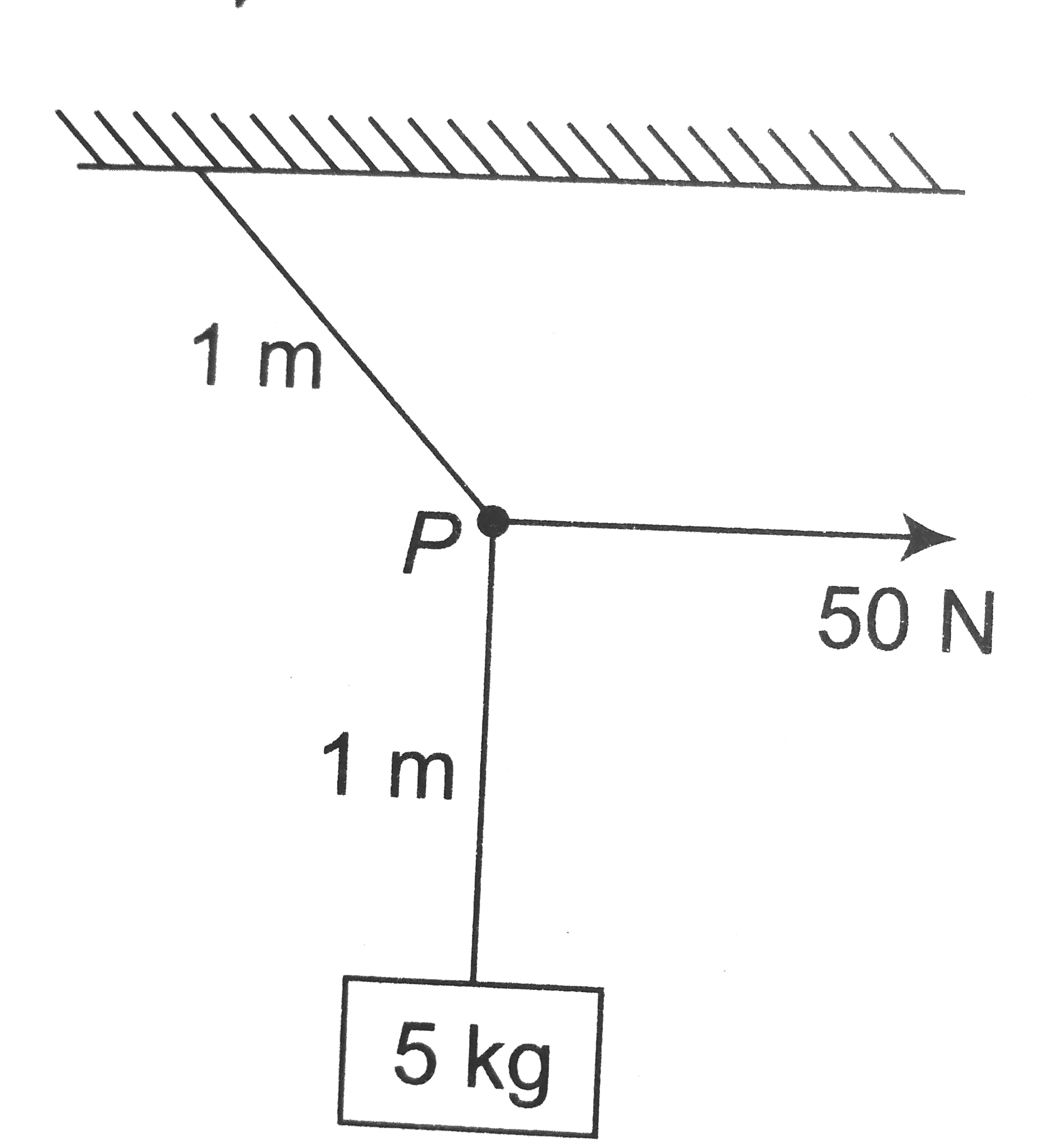 A30∘B40∘C60∘D45∘
A30∘B40∘C60∘D45∘
A mass of 10 kg is suspended vertically by a rope from the roof. When a horizontal force is applied on the rope at some point, the rope deviated at an angle of 45∘ at the roof point. If the suspended mass is at equilibrium, the magnitude of the force applied is (g=10ms−2)
View SolutionA mass of 10 kg is suspended vertically by a rope from the roof. When a horizontal force is applied on the rope at some point, the rope deviated at an angle of 45∘ at the roof point. If the suspended mass is at equilibrium, the magnitude of the force applied is (g=10ms−2)
View SolutionA mass M is suspended by a rope from a rigid support at A as shown in figure. Another rupe is tied at the end B, and it is pulled horizontally with a force. If the rope AB makes an angle θ with the vertical in equilibrium then the tension in the string AB is
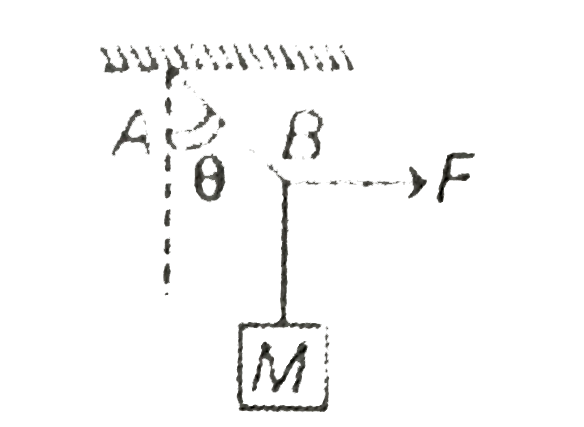
View SolutionA 10 kg body is suspended by a rope is pulled by means of a horizontal force to make 60° by rope to vertical. The horizontal force is
View SolutionA horizontal uniform rope of length L, resting on a frictionless horizontal surface, is pulled at one end by force F. What is the tension in the rope at a distance l from the end where the force is applied?
View SolutionA block of mass 10 kg lying on a smooth horizontal surface is being pulled by means of-a rope of mass 2 kg. If a force of 36N is applied at the end of the rope, the tension at the mid point of the rope is,
View SolutionA block is lying on the horizontal frictionless surface. One end of a uniform rope is fixed to the block which is pulled in the horizontal direction by applying a force F at the other end. If the mass of the rope is half the mass of the block. The tension in the middle of the rope will be
View Solution
