A mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the UV to the end of the red visible spectrum. In our experiment with rubidium photocell, the following lines from a mercury source were used: $λ_{1} = 3650 A^{\circ}, λ_{2} = 4047 A^{\circ}, λ_{3} = 4358 A^{\circ}, λ_{4} = 5461 A^{\circ}, λ_{5} = 6907 A^{\circ}$ The stopping voltages, respectively were measured to be:
$V_{01} = 1.28 V, V_{02} = 0.95 V, V_{03} = 0.74 V, V_{04} = 0.16 V, V_{05} = 0 V$ .
(a) Determine the value of Planck's constant h.
(b) Estimate the threshold frequency and work function for the material.

Video Solution

Text Solution

Verified by Experts

Einstein's photoelectric equation is given as:
$e V_{0} = h v - ϕ_{0}$
$V_{0} = \frac{h}{e} v - \frac{{(ϕ)}_{0}}{e} ... . (1)$
Where,
$V_{0}$ = Stopping potential
$h =$ planck's constant
$e =$ Charge on an electron
$v =$ Frequency of radiation
$ϕ_{0}$ = work function of a material
It can be concluded from equation (1) that potential $V_{0}$ is directly proportional to frequency v.
Frequency is also given by the relation:
$v = \frac{Speed of light (c)}{Wavelength (λ)}$
This relation can be used to obtain the frequencies of the various lines for the given wavelengths.
$v_{1} = \frac{c}{{(λ)}_{1}} = \frac{3 \times 10^{8}}{3650 \times 10^{- 10}} = 8.219 \times 10^{14} H z$
$v_{2} = \frac{c}{{(λ)}_{2}} = \frac{3 \times 10^{8}}{4047 \times 10^{- 10}} = 7.412 \times 10^{14} H z$
$v_{3} = \frac{c}{{(λ)}_{3}} = \frac{3 \times 10^{8}}{4358 \times 10^{- 10}} = 6.884 \times 10^{14} H z$
$v_{4} = \frac{c}{{(λ)}_{4}} = \frac{3 \times 10^{8}}{5461 \times 10^{- 10}} = 5.493 \times 10^{14} H z$
$v_{5} = \frac{c}{{(λ)}_{5}} = \frac{3 \times 10^{8}}{6907 \times 10^{- 10}} = 4.343 \times 10^{14} H z$
The given quantities can be listed in tabular form as:

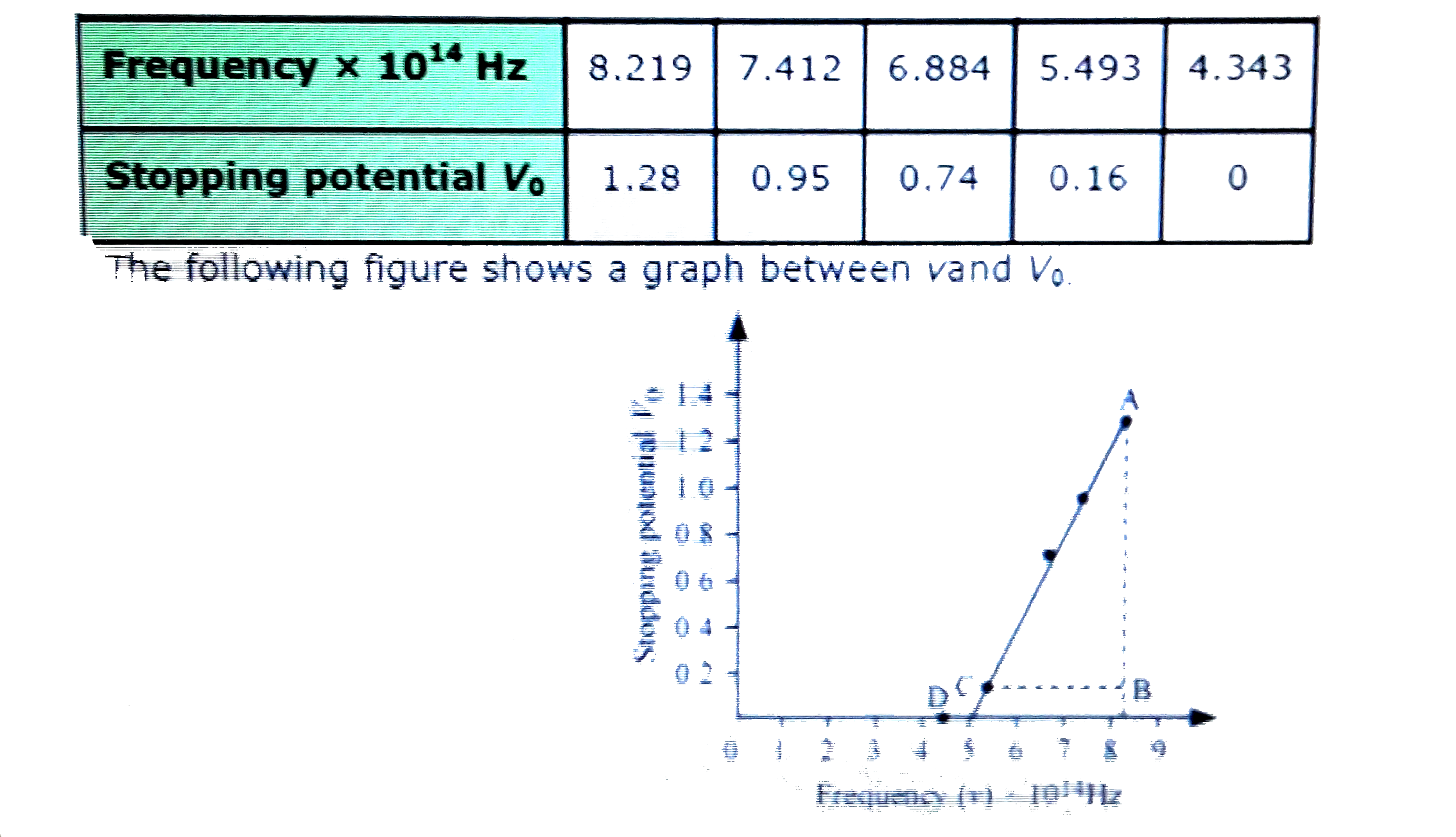
The following figures shows a graph between v and $V_{0}$ .
It can be observed that the obtained curve is a stright line. It intersects the v-axis at $5 \times 10^{14} H z$ , which is the threshold frequency $(v_{0})$ of the material. Point D corresponds to a frequency less than the threshold frequency. Hence, there is no photoelectric emission for the $λ_{5}$ line, and therefore, no stopping voltages is required to stop the current.
Slope of the straight line $= \frac{A B}{C B} = \frac{1.28 - 0.16}{(8.214 - 5.493) \times 10^{14}}$
From equation (1), the slope $\frac{h}{e}$ can be written as:
$\frac{h}{v} = \frac{1.28 - 0.16}{(8.214 - 5.493) \times 10^{14}}$
$∴ h = \frac{1.12 \times 1.6 \times 10^{- 19}}{2.726 \times 10^{14}}$
$= 6.573 \times 10^{- 34} J s$
The work fuction of the metal is given as:
$ϕ_{0} = h v_{0}$
$= 6.573 \times 10^{- 34} \times 5 \times 10^{14}$
$= 3.286 \times 10^{- 19} J$
$= \frac{3.286 \times 10^{- 19}}{1.6 \times 10^{- 18}} = 2.054 e V$

Updated on:21/07/2023