A metal rod of cross sectional area 1.0cm2 is being heated at one end. At one time , the temperature gradient is 5.0∘Ccm−1 at cross section A and is 2.5∘Ccm−1 at cross section B. calculate the rate at which the temperature is increasing in the part AB of the rod. The heat capacity of the part AB=0.40J∘C−1 , thermal conductivity of the material of the rod. K=200Wm−1C−1 . Neglect any loss of heat to the atmosphere.
The correct Answer is:A, B, C
The rate of heat flow per sec
dQAdt=KAd(θA)dl
The rate of heat flow per sec
dQBdt=KAd(θB)dl
the part of heat is absorbed by the rod.Qt=msΔθdt
where dθdt= Rate of tempareture variation .
⇒msΔθdt=KAd(θA)dl−KAd(θB)dl,
⇒msdθdt=KA(d(θA)dl−d(θB)dl)
⇒0.4dθdt=200×2.5×10−4
(5−2.5)∘C/cm.
⇒dθdt=200×2.5×10−40.4×10−2
=1250×10−2=12.50Cs.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - QUESTIONS FOR SHORT ANSWER11videos
HEAT TRANSFER
- BOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - OBJECTIVE II6videos
HEAT TRANSFER
- BOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 26videos
HEAT AND TEMPERATURE
- BOOK - HC VERMA ENGLISHCHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Question for short Answer4videos
INTRODUCTION TO PHYSICS
Similar Questions
Find the rate of heat flow through a cross section of the rod shown in figure (θ2>θ1) . Thermal conductivity of the material of the rod is K.
 View Solution
View SolutionA metal rod of length 'L' and cross-sectional area 'A' is heated through 'T'∘C What is the force required to prevent the expansion of the rod lengthwise ?
View SolutionFind the thermal resistance of an aluminium rod of length 20cm and area of cross section 1cm2 . The heat current is along the length of the rod. Thermal conductivity of aluminium =200Wm−1K−1 .
View SolutionAn irregular rod of same uniform material as shown in figure is conducting heat at a steady rate. The temperature gradient at various sections versus area of cross section graph will be
_S01_094_Q01.png) View Solution
View SolutionThe left end of a copper rod (length=20cm, Area of cross section=0.2cm2) is maintained at 20∘C and the right end is maintained at 80∘C . Neglecting any loss of heat through radiation, find (a) the temperature at a point 11cm from the left end and (b) the heat current through the rod. thermal conductivity of copper =385Wm−1C−1 .
View SolutionDue to a spatial variation in purity, the thermal conductivity of a metal bar (cross sectional area 4×10−4m2, length 1m) decreases linearly along its length from 400 Wm−1K−1 at one end, to 200 Wm−1K−1 at the other. Calculate the rate at which heat flows through the bar if the hot end is maintained at 200∘C and the cold end at 0∘C
View SolutionTwo rods A and B of same cross-sectional area A and length l are connected in series between a source (T1=100∘C) and a sink (T2−0∘C) as shown in figure. The rod is laterally insulated.
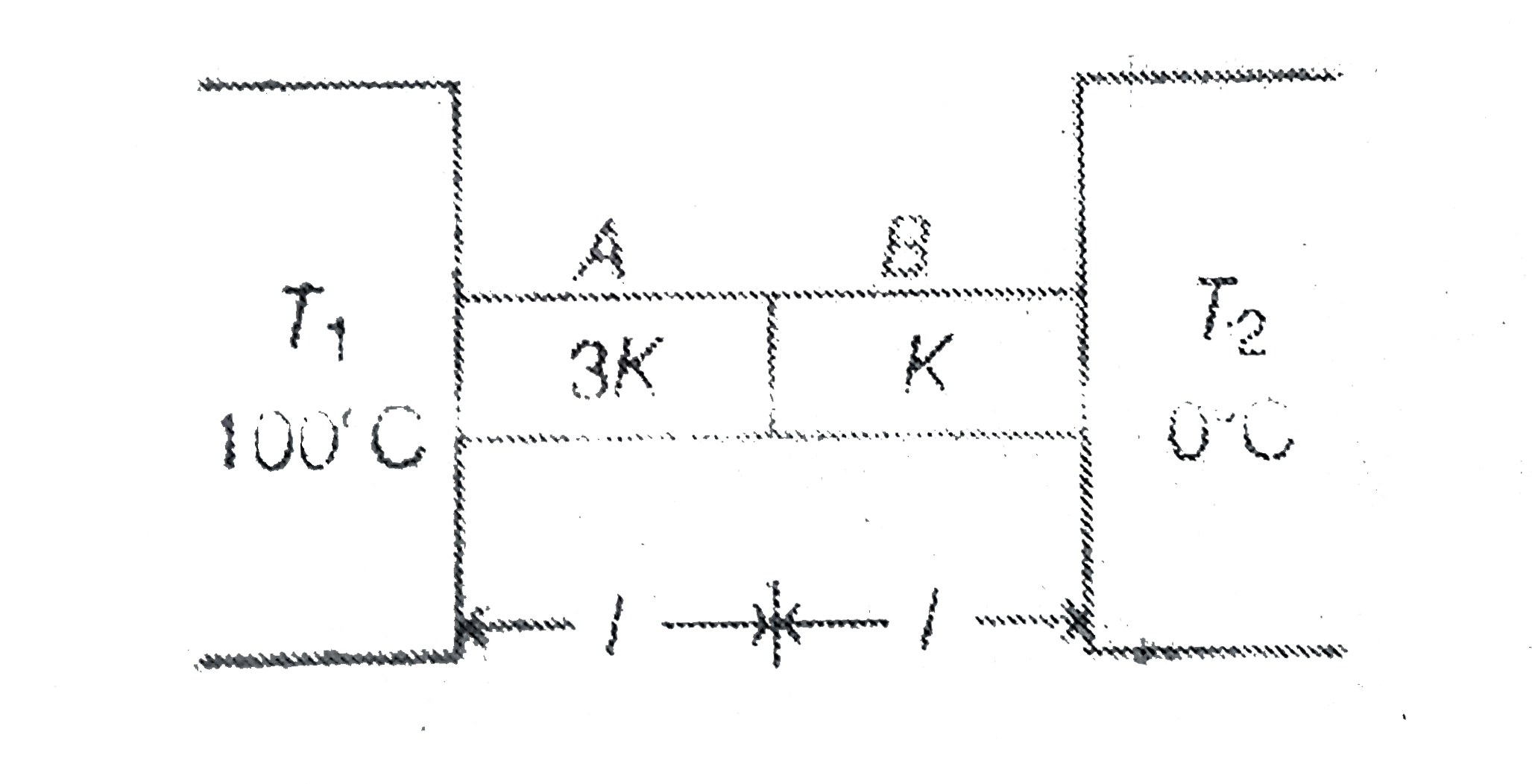
If GA and GB are the temperature gradients across the rod A and B, thenView SolutionThree rods of material x and three of material y are connected as shown in figure. All the rods are identical in length and cross sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C , calculate the temperature of the junction B. The thermal conductivity of x is 800Wm−1C−1 and that of y is 400Wm−1C−1 .
 View Solution
View SolutionThree rods of material x and three of material y are connected as shown in figure. All the rods are identical in length and cross sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C , calculate the temperature of the junction B. The thermal conductivity of x is 800Wm−1.∘C−1 and that of y is 400Wm−1.∘C−1 .
 View Solution
View SolutionThe ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.
View Solution

