A mild steel wire of length 1.0 m and cross-sectional are 0.5×10−20cm2 is streached, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid point of the wire, calculate the depression at the mid point.
g=10ms−2,Y=2×1011Nm−2.
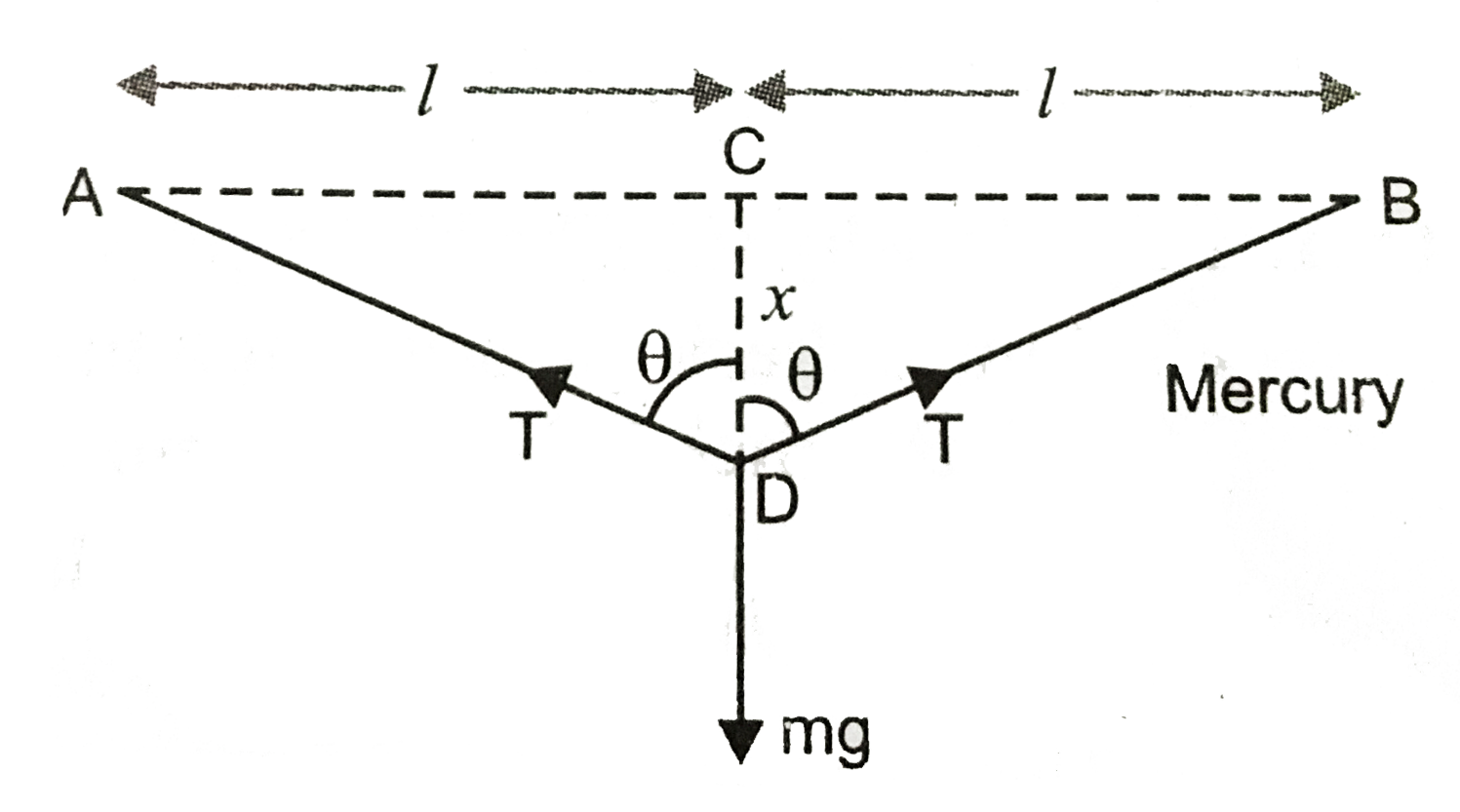
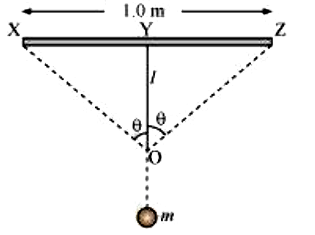
Length of the steel wire = 1.0 m
Area of cross-section, A = 0.50 ×10−2cm2=0.50×10−6m2
A mass 100 g is suspended from its midpoint.
m = 100 g = 0.1 kg
Hence, the wire dips, as shown in the given figure.
Original length = XZ
Depression = l
The length after mass m, is attached to the wire = XO + OZ
Increase in the length of the wire:
Δl=(XO+OZ)−XZ
Where, XO=OZ=[(0.5)2+l2]12
∴Δl=2[(0.5)2+(l)2]12−1.0
2×0.5[1+(l0.5)2]12−1.0
Expanding and neglecting higher terms, we get:
Δl=l20.5
Strain = Increase in lengthOriginal length
Let T be the tension in the wire.
∴mg=2Tcosθ
Using the figure, it can be written as:
cosθ=l((0.5)2+l2)12
=l(0.5)(1+(l0.5)2)12
Expanding the expression and eliminating the higher terms:
cosθ=l(0.5)(1+l22(0.5)2)
(1+l20.5)≅1 for small l
∴cosθ=l0.5
∴T=mg2(l0.5)=mg×0.52l=mg4l
Stress = TensionArea=mg4l×A
Young's modulus = =StressStrain
Y=mg×0.54l×A×l2
l=3√mg×0.54YA
Young’s modulus of steel, Y= 2×1011 Pa
∴l=√0.1×9.8×0.54×2×1011×0.50×10−6
= 0.0106 m
Hence, the depression at the midpoint is 0.0106 m.
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE21videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NCERTCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - EXERCISE31videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NCERTCHAPTER - MOTION IN A PLANE EXERCISE - EXERCISE32videos
MOTION IN A PLANE
Similar Questions
A steel wire of length 4.7m and cross-sectional area 3×10−6m2 stretches by the same amount as a copper wire of length 3.5m and cross-sectional area of 4×10−6m2 under a given load. The ratio of Young's modulus of steel to that of copper is
08:31View SolutionExplain why (a) the blood pressure is humans is greater at the feet than at the brain.
(b) Atmospheric pressure at a height of about 6 km decreases to nearly half its value at the sea level through the 'height' of the atmospheric is more than 100 km.
(c) Hydrostatic pressure is a scalar quantity even though pressure is force divided by area , and force is a vector.15:12View SolutionState, for each of the following physical quantities, if it is a scalar or a vector. Volume, mass speed acceleration, density, number of moles, velocity, angular frequency, displacement, angular velocity.
02:37View SolutionA mild steel wire of length 1.0 m and cross-sectional are 0.5 xx 10^(-20)cm^(2) is streached, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid point of the wire, calculate the depression at the mid point. g = 10ms^(-2), Y=2 xx 10^(11)Nm^(-2 .
View SolutionA mild steel wire of length 1.0m and cross sectional area 5.0×10−2cm2 is stretched, within its elastic limit horizontally between two pillars. A mass of 100g is suspended form the midpont of the wire. Calculate the depression at the midpoint (Ysteel=200GPa)
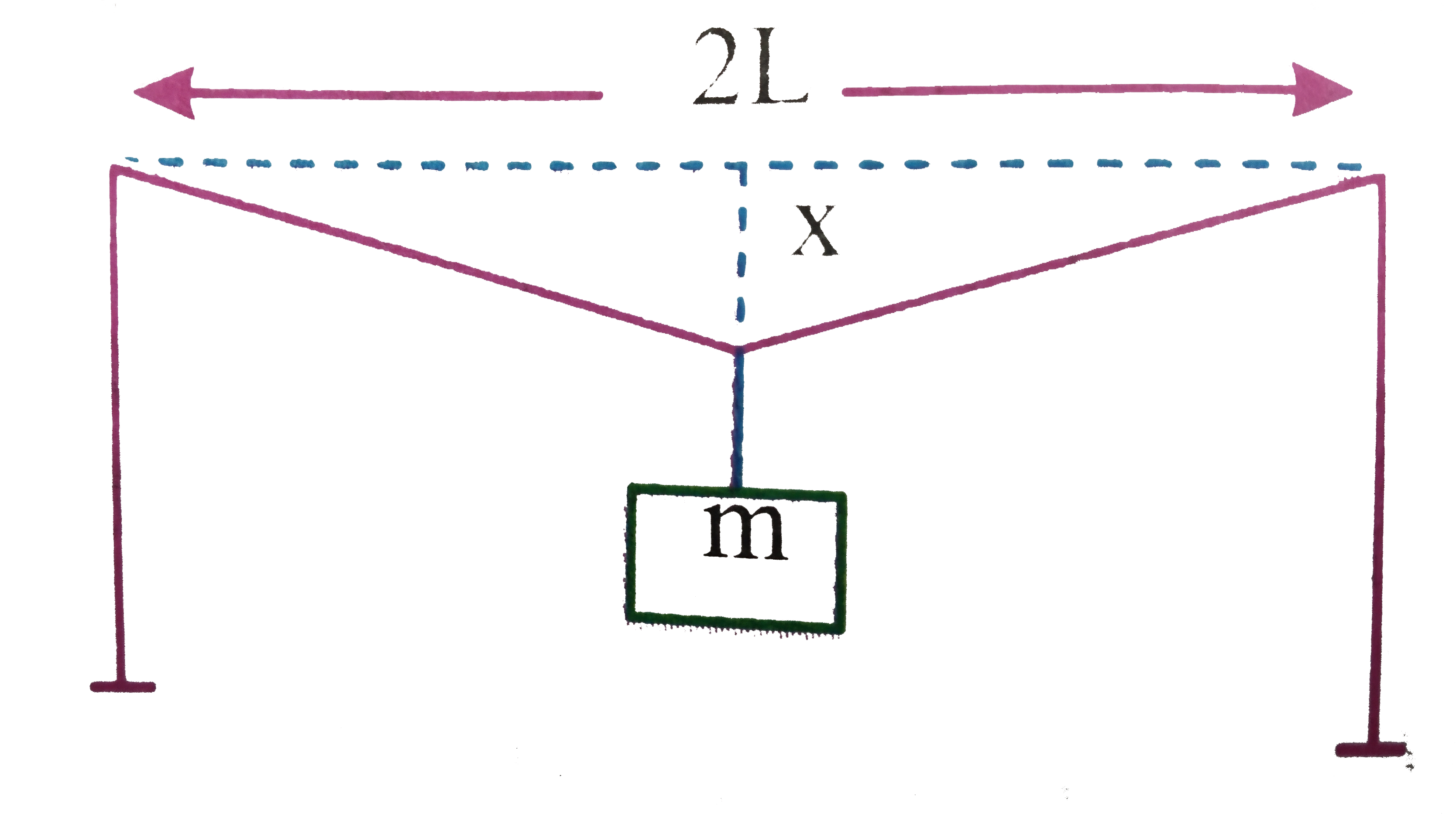
View SolutionA mild steel wire of length 1.0m and cross sectional area 2L is strethched, within its elastic limit horizontally between two pillars(figure). A mass of m is suspended form the midpont of the wire. Strain in the wire is
View SolutionA mild steel wire of Length 2L and cross sectional Area A is stretched well within elastic limit, horizontally between two pillars. A man m is suspended from the mid point of the wire strain in the wire is
View SolutionA mild steel wire of length 1.0 m and cross sectional area 0.50 times 10^-2 (cm)^2 is stretched , well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid-point of the wire. Calculate the depression at the mid -point.
View SolutionA mild steel wire of length 1.0 m and cross - sectional area 0.50xx10^(-2)" cm"^(2) is stretched, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid - point of the wire. Calculate the depression at the mid point.
07:17View SolutionA mild steel wire of length 1.0 m and cross - sectional area 0.50xx10^(-2)" cm"^(2) is stretched, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid - point of the wire. Calculate the depression at the mid point.
10:10View SolutionA mild steel wire of length 1.0 m and cross - sectional area 0.50×10−2 cm2 is stretched, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid - point of the wire. Calculate the depression at the mid point.
04:42View SolutionA mild steel wire of length 1.0 m and cross - sectional area 0.50xx10^(-2)" cm"^(2) is stretched, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid - point of the wire. Calculate the depression at the mid point.
05:58View SolutionA mild steel wire of length 1.0 m and cross sectional area 0.50×10−2cm2 is stretched, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid-point of the wire. Calculate the depression at the midpoint.
07:28View SolutionA mild steel wire of length 2L and crosssectional area A is stretched, well within elastic limit, horizontally between two pillars as shown in figure. A mass m is suspended from the mid point of the wire, the mid point lower by distance x. Then strain in the wire is ......
View SolutionA mild steel wire of length 1.0m and cross sectional area 2L is strethched, within its elastic limit horizontally between two pillars(figure). A mass of m is suspended form the midpont of the wire. Strain in the wire is
 View Solution
View SolutionA mild steel wire of length 2L and cross sectional area A is stretched, well within elastic limit, horizontally between two pillars. A mass m is suspended from the mid point of the wire. The mid point is lowered by x. Strain in the wire is
View Solution

