A nail is fixed up perpendicularly at the centre of a circular wooden plate. Keeping the nail at bottom, the circular plate is made of float in water. What should be the maximum ratio of the radius of the plate and length of the nail so that the nail wil be out of vision? Refractive index of water = .
AB is the circular wooden plate and CD is the nail. Suppose, radius of the plate = r and the length of the nail = h [Fig. 2.30]. Since the nail is not seen from air, the angle of incidence of the ray DA will be greater than and the ray will be totally reflected.
This is the required ratio. 
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - HIGHER ORDER THINKING SKILL (HOTS QUESTION)
25 Videos
- REFRACTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - SECTION RELATED QUESTION
18 Videos
- REFLECTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFLECTION OF LIGHTEXERCISE - INTEGER ANSWER TYPE
3 Videos
- SEMICONDUCTORS AND ELECTRONICS BOOK - CHHAYA PUBLICATIONCHAPTER - SEMICONDUCTORS AND ELECTRONICS EXERCISE - CBSE SCANNER
31 Videos
Similar Questions
A microscope is focussed on a coin lying at the bottom of a beaker. The microscope is now raised up by 1cm. To what depth should the water be poured into the beaker so that coin is again in focus ? (Refration index of water is 4/3)
View SolutionA beam of light travelling in water strikes a glass plate, which is also immersed in water. When the angle of incidence is 51∘, the reflected beam is found to be plane polarised . What is the refractive index of glass if the refractive index of water is 43? [tan51∘=1.235]
View Solution
Knowledge Check
A microscope is focused on a coin lying at the bottom of a beaker. The microscope is now raised up by 1cm. To what depth should the water be poured into the beaker so that coin is again in focus ? (Refractive index of water is 4/3)
A1cmB4/3cmC3cmD4cmA beam of light travelling in water strikes a glass plate, which is also immersed in water. When the angle of incidence is 51∘, the reflected beam is found to be plane polarised . What is the refractive index of glass if the refractive index of water is 43? [tan51∘=1.235]
A1.646B1.325C2.123D1.987
A container contains water up to a height of 20 cm and there is a point source at the centre of the bottom of the container. A rubber ring of radius r floats centrally on the water. The ceiling of the room is 2.0 m above the water surface. (a) Find the radius of the shadow of the ring formed on the ceiling if r = 15 cm. (b) Find the maximum value of r for which the shadow of the ring is formed on the ceiling. Refractive index of water =4/3.
View SolutionA container contains water up to a height of 20 cm and there is a point source at the centre of the bottom of the container. A rubber ring of radius r floats centrally on the water. The ceiling of the room is 2.0 m above the water surface. (a) Find the radius of the shadow of the ring formed on the ceiling if r = 15 cm. (b) Find the maximum value of r for which the shadow of the ring is formed on the ceiling. Refractive index of water =4/3.
View SolutionA small object is placed at the centre of the bottom of a cylindrical vessel of radius 3 cm and height 4 cm filled completely with water. Consider the ray leaving the vessel through a corner. Suppose this ray and the ray along the axis of the vessel are used to trace the image. Find the apparent depth of the image and the ratio of real depth to the apparent depth under the assumptions taken. Refractive index -of water = 1-33.
View SolutionA small object is placed at the centre of the bottom of a cylindrical vessel of radius 3 cm and height 4 cm filled completely with water. Consider the ray leaving the vessel through a corner. Suppose this ray and the ray along the axis of the vessel are used to trace the image. Find the apparent depth of the image and the ratio of real depth to the apparent depth under the assumptions taken. Refractive index -of water = 1-33.
View SolutionA cubical vessel with non-transparent walls is so located that the eye of an observer does not see its bottom but sees all of the wall CD.
To what height should water be poured into the vessel for the observer to see an object F arranged at a distance of b=10cm from corner D? The face of the vessel is a=40cm. Refractive index of water is 43.
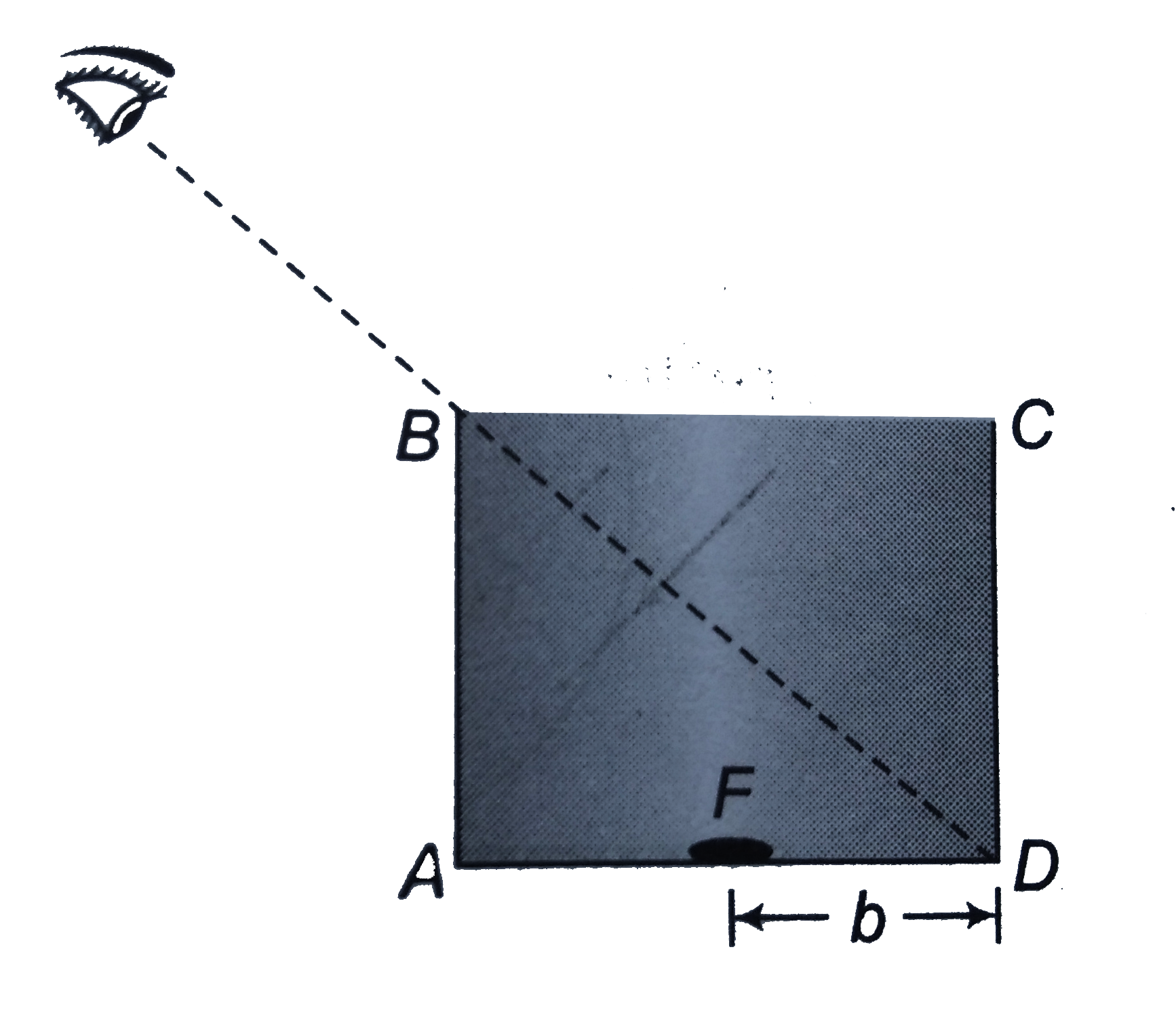
View SolutionA cubical vessel with non-transparent walls is so located that the eye of an observer does not see its bottom but sees all of the wall CD.
To what height should water be poured into the vessel for the observer to see an object F arranged at a distance of b=10cm from corner D? The face of the vessel is a=40cm. Refractive index of water is 43.

View Solution
