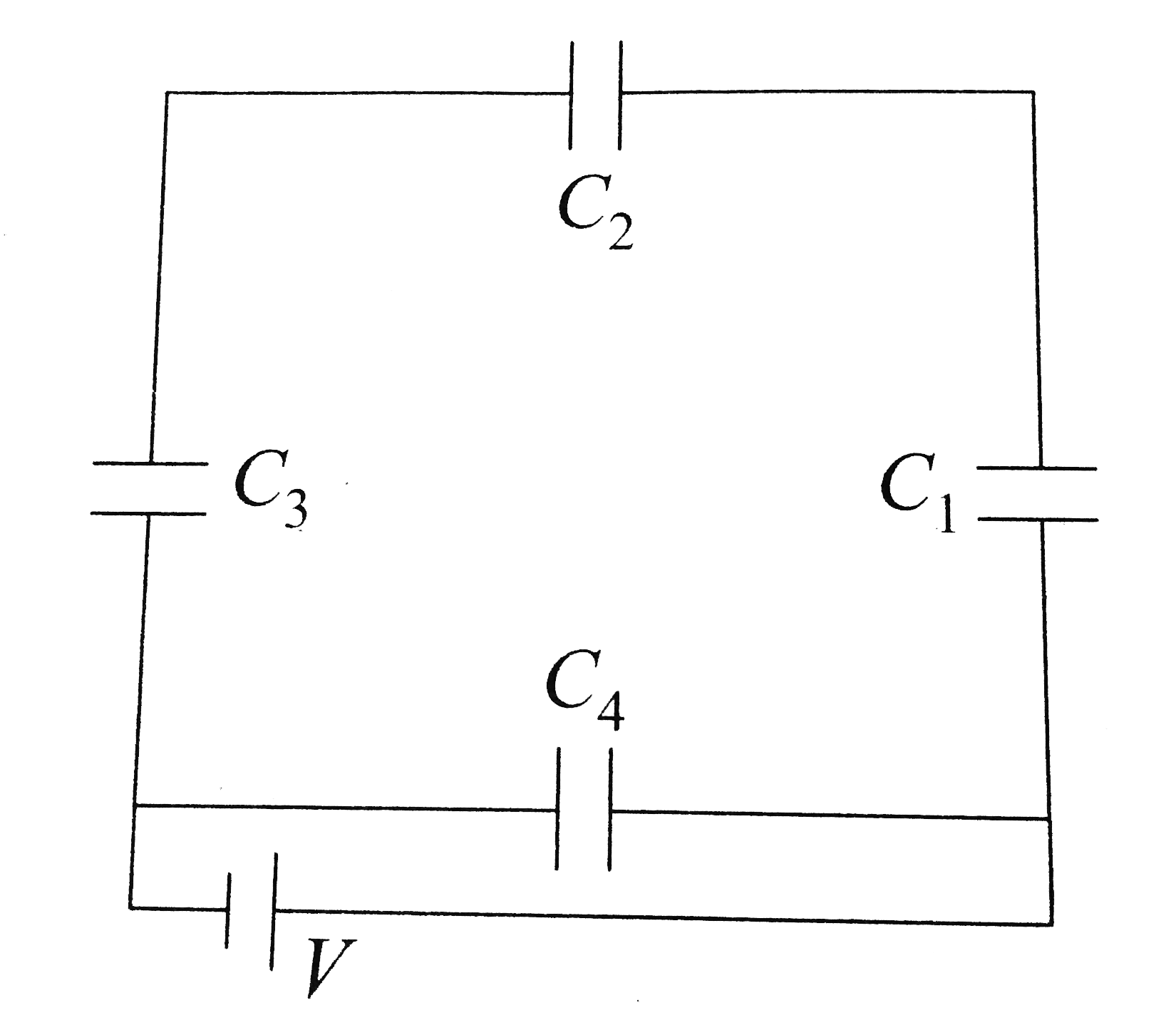
A network of four capacitors of capacity equal to C1=C,C2=2C,C3=3C and C4=4C are connected to a battery as shown in the figure. The ratio o fthe charges on C2 an C4 is
47
322
74
223
The correct Answer is:B

C1,C2,C3 are in series,
∴1CS=1C+12C+13C
=6+3−26C=116C
∴CS=6C11
When the capacitors are in series, each capacitor has the same charge.
Thus, q1=q2=q3=CS×V=6CV11
and the charge on C4 is Q4=(4C)V=4CV
∴q2q4=6CV11×14CV=322.
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - TEST YOUR GRASP20videos
ELECTROSTATICS
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTRONS AND PHOTONS EXERCISE - TEST YOUR GRASP - 1715videos
ELECTRONS AND PHOTONS
- BOOK - MARVEL PUBLICATIONCHAPTER - GRAVITATION EXERCISE - TEST YOUR GRASP -220videos
GRAVITATION
Similar Questions
Knowledge Check
- Question 1 - Select One
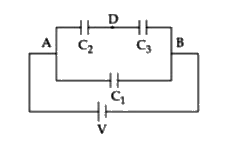
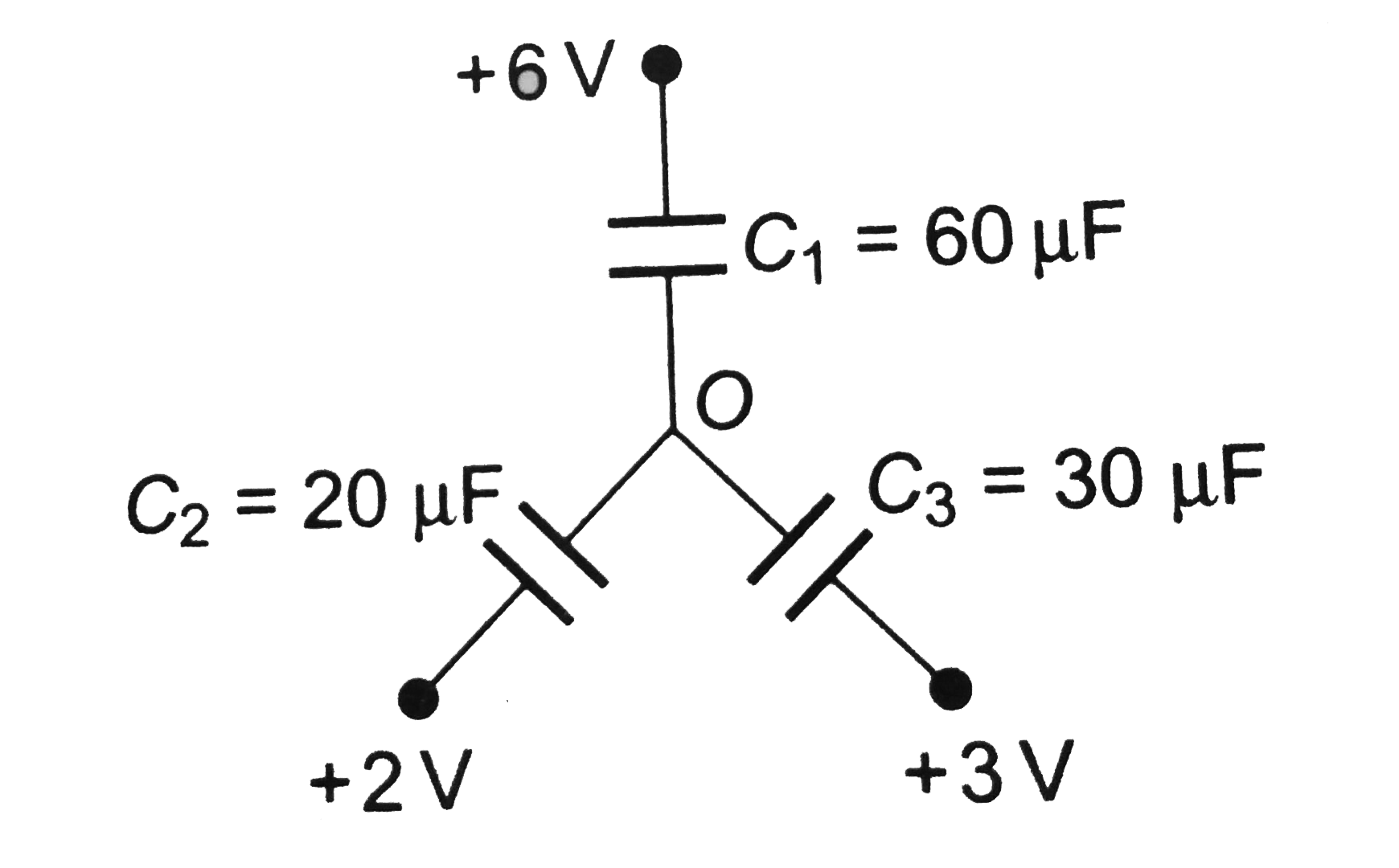
Three uncharged capacitors of capacitance C1,C2 and C3 are connected to one another as shown in figure. The potential at O will be
 A3VB4911VC4VD311V
A3VB4911VC4VD311V - Question 2 - Select One
Find the charge on capacitor C3
Given, then C1=C2andC3=C4 = 3 C .
 A32 CVBCV2C3 CVD2CV
A32 CVBCV2C3 CVD2CV - Question 3 - Select One or More
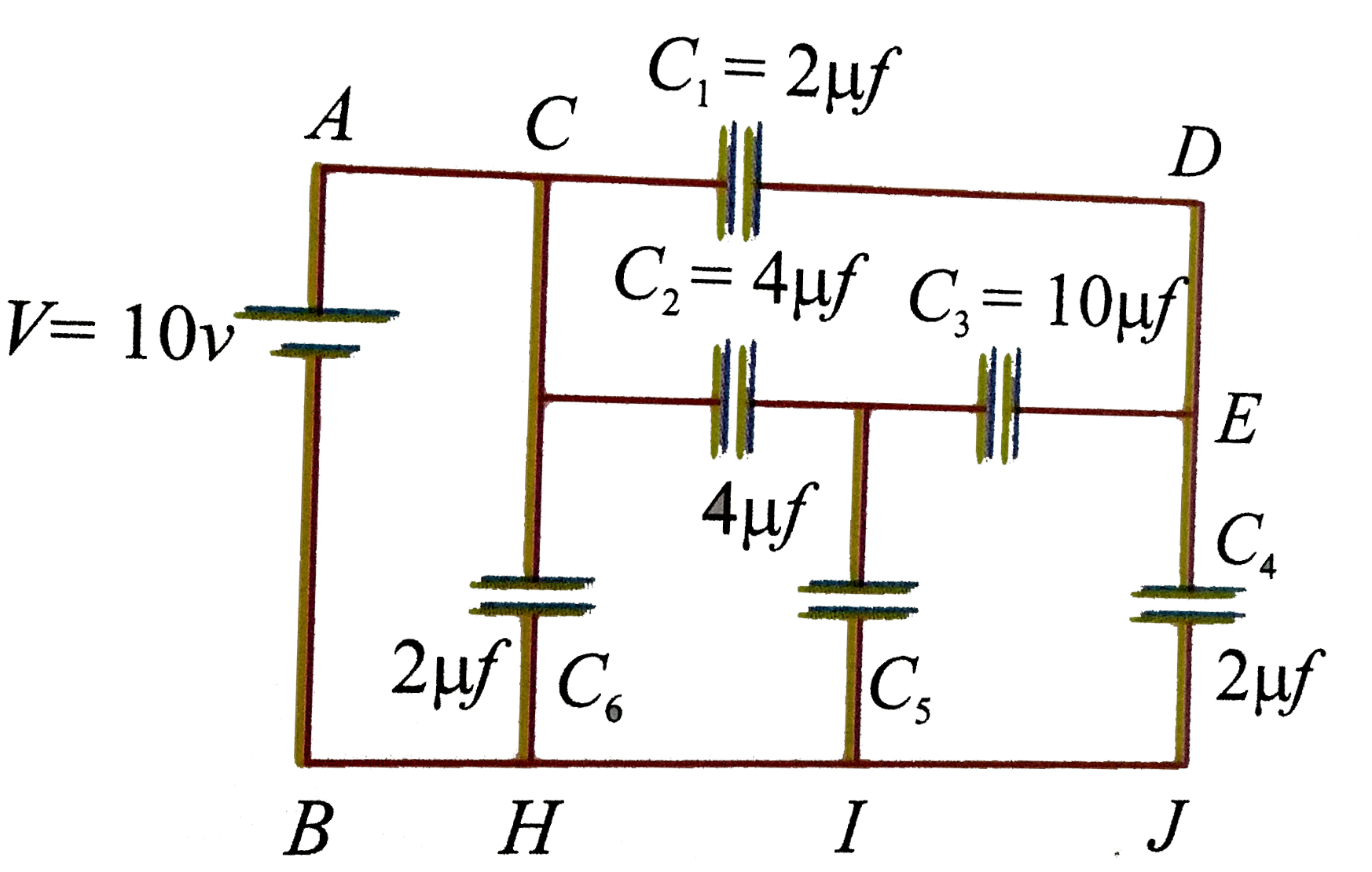
In the given circuit, find the charge on C1,C2,C3,C4 and C5. A battery is connected as shown in the figure.
 .
.
Select of correct options.AThe charge on C1=10μCBThe charge on C2=20μCCThe charge on C3=zeroDThe charge on C4=10μC
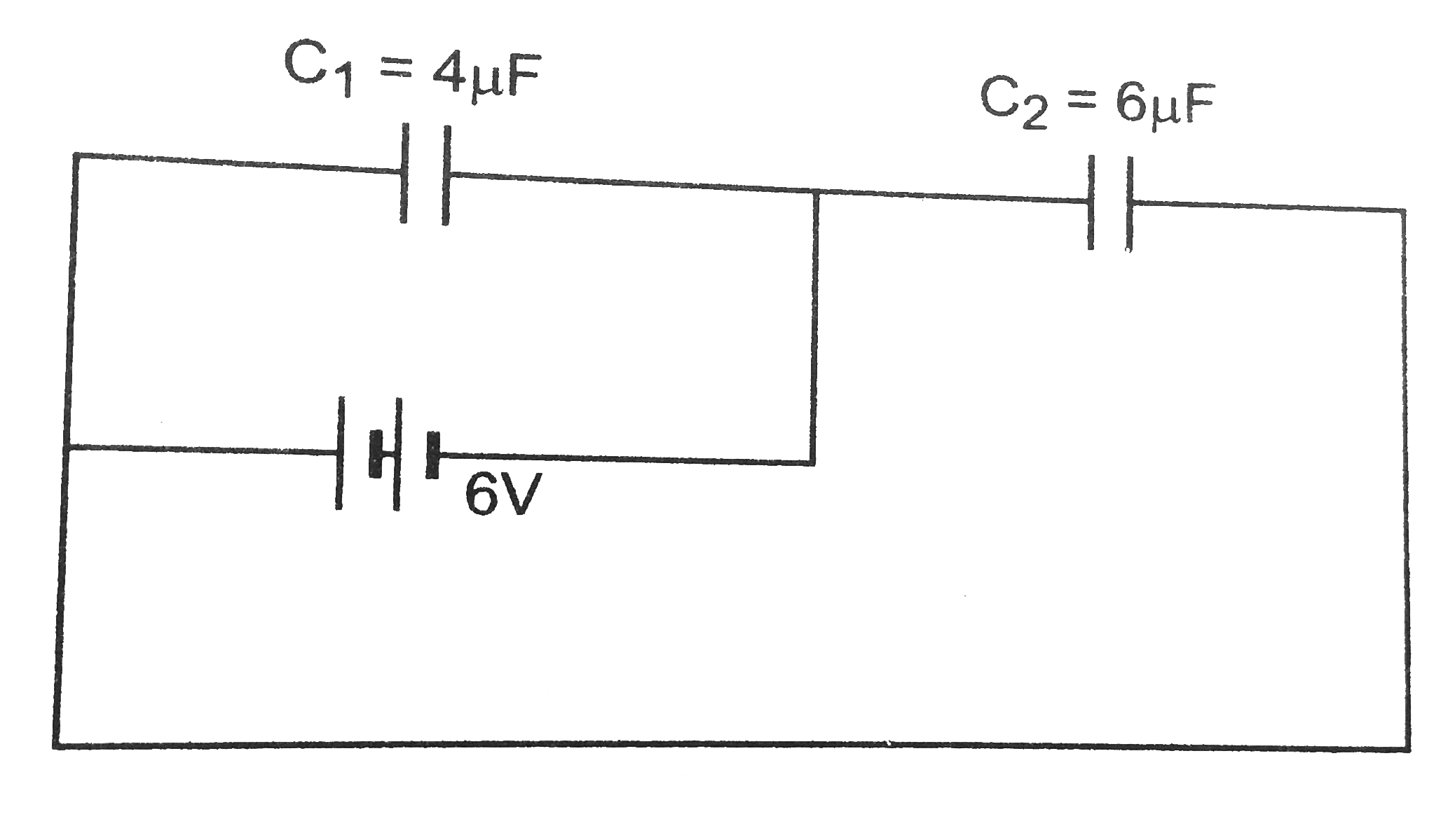
Three capacitors C1,C2andC3 are connected to a 6 V battery, as shown in Fig. Find the charges on the three capcitors.
 View Solution
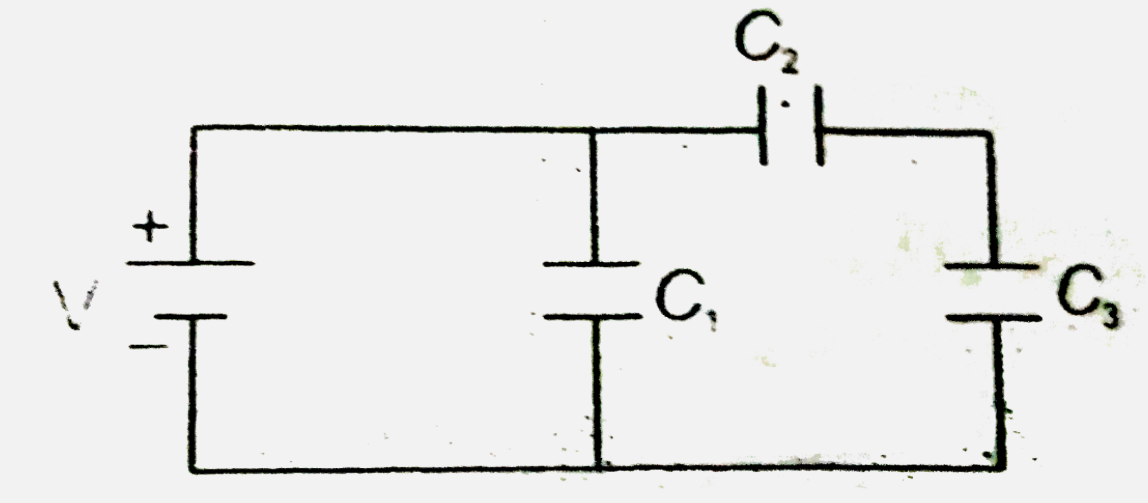
View SolutionThree capacitors C1,C2 and C3 are connected to a battery as shown in the figure . The three capacitors have equal capacitances. Which capacitor stores the most energy ?
 View Solution
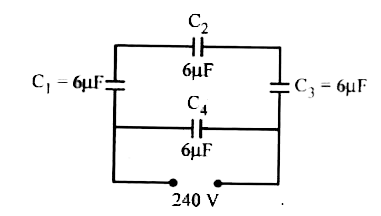
View SolutionA network of 4 capacitors, each of 6μF is connected to a 240 V supply as shown in the figure. What are the charges on the capacitor C2andC4 ?
 View Solution
View SolutionFour capacitors C1=8μF,
C2=2μf,C3=6μF, and C4=6,μF are arranged as shown in. Find the charge on all the capacitors in the circuit.
 .View Solution
.View SolutionFive capacitors of capacitances C1=C5=1μF,C2=C3=C4=2μF are connectes as shown in Fig. Calculate equivalent capacitance of the system between points A and B.
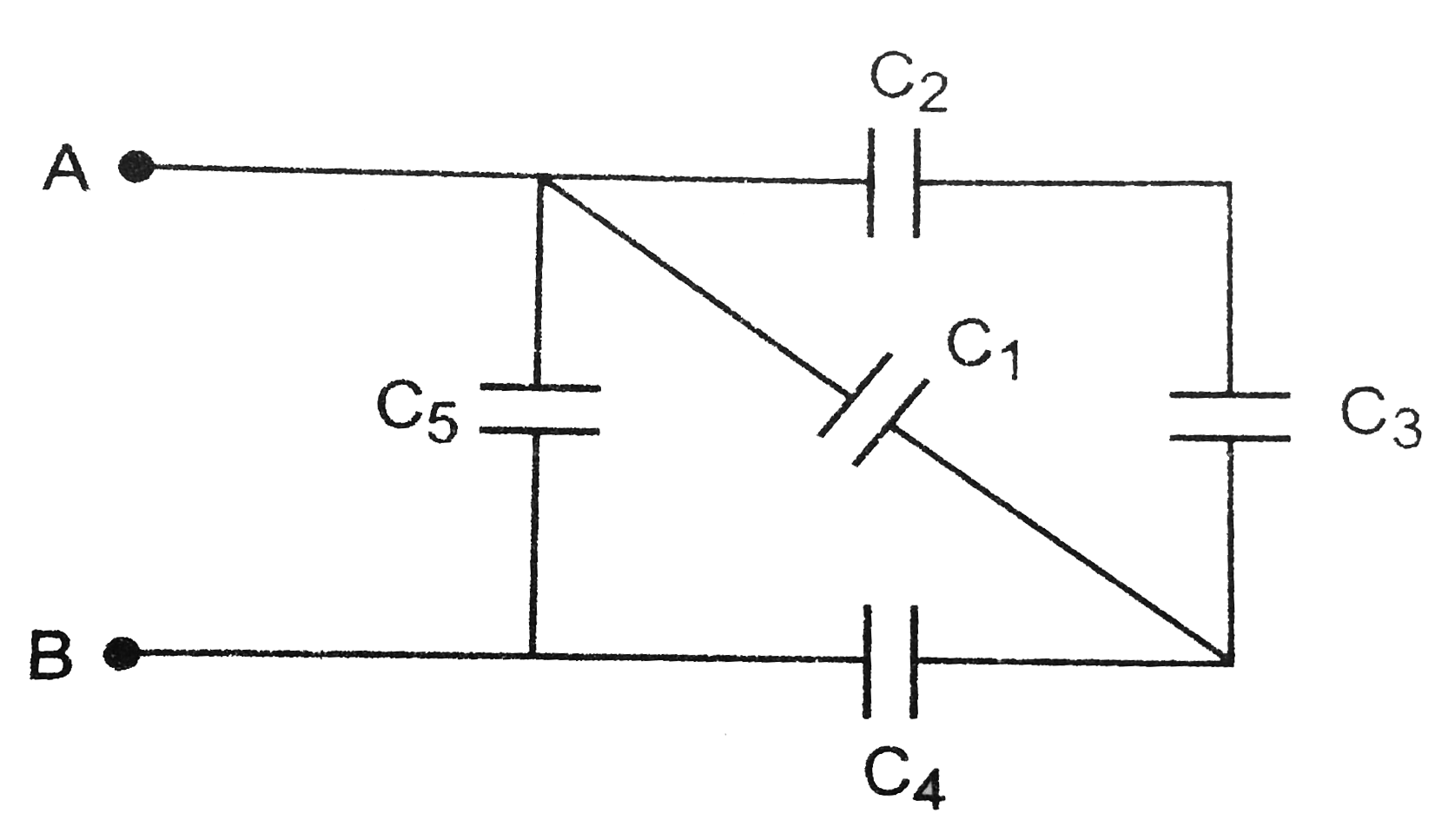 View Solution
View Solution