A nuclear reaction is given as
$A + B \to C + D$
Binding energies of $A, B, C,$ and $D$ , are given as $B_{1}, B_{2}, B_{3}$ and $B_{4}$ . Find the energy released in the reaction.

Video Solution

Text Solution

Verified by Experts

$(B_{3}_B_{4}) - (B_{1} + B_{2})$

Updated on:21/07/2023

In the reaction sequences
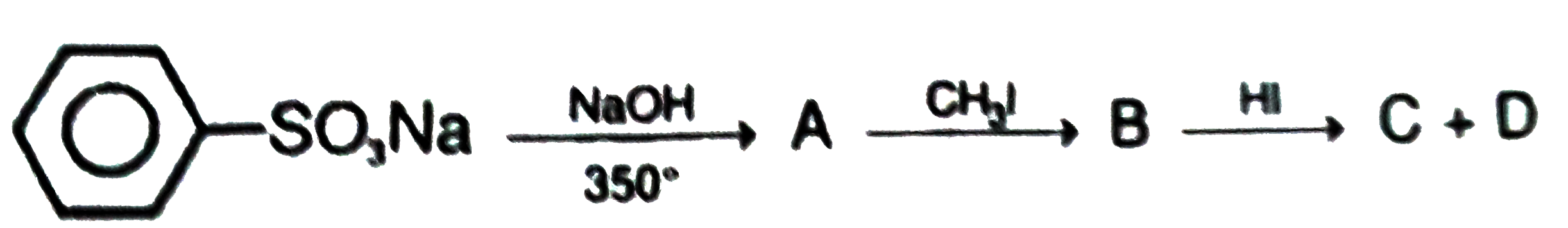
A,B,C and D are given by the set:
ASodium phenate, anisole, $C_{6} H_{5} l, C H_{3} O H$
BSodium phentate, phenitole, $C_{2} H_{5} l, C_{6} H_{5} O H$
CSodium phenate, anisole, $C_{6} H_{5} O H, C H_{3} l$
DSodium phenate, phenitole, $C_{6} H_{5} l, C_{2} H_{5} O H$
Consider the nuclear reaction $X^{200} \to A^{110} + B^{80}$ . The binding energy per nucleon for X, A and B are 7.4 MeV, 8.2 MeV and 8.1 MeV respectively. What is the energy released in the nuclear reaction ?
Aa) 380 MeV
Bb) 190 MeV
Cc) 100 MeV
Dd) 70 MeV
In the reaction $._{1}^{2} H + ._{1}^{3} H \to ._{2}^{4} H e + ._{0}^{1} n$ , if the binding energies of $._{1}^{2} H, ._{1}^{3} H$ and $._{2}^{4} H e$ are respectively $a, b$ and $c$ (in MeV), then the energy (in MeV) released in this reaction is.
A $c + a - b$
B $c - a - b$
C $a + b + c$
D $a + b - c$