A particle is thrown with a velocity 10m/s and its horizontal range is 5m. Find angle/angles of the projection.
R=u2gsin2θ
5−(10)210=sin2θ⇒2θ=12=sin30∘
2θ=30∘⇒θ=15∘
Another angle of projection will be 90−θ=75∘.
Angles of projection: 15∘ and 75∘.
Topper's Solved these Questions
Similar Questions
A ball projected with a velocity of 28 m/sec has a horizontal range 40 m. Find the two angles of projection.
View SolutionA particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View Solution
Knowledge Check
A particle is thrown with the velocity v with the angle α from the horizontal plane and its range on the horizontal plane is twice to the maximum height gained. Thentanα is equal to
A9B5C2D1A particle is thrown with the velocity v with the angle α from the horizontal plane and its range on the horizontal plane is twice to the maximum height gained. Thentanα is equal to
A9B5C2D1A particle is thrown at time t=0 with a velocity of 10 m/s at an angle of 60∘ with the horizontal from a point on an incline plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is :
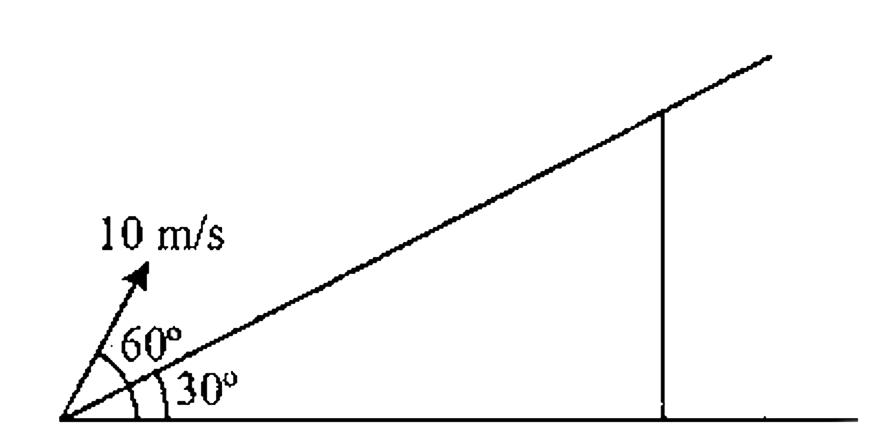 A2√3 secB1√3 secC√3 secD12√3 sec
A2√3 secB1√3 secC√3 secD12√3 sec
A ball is thrown such that the time of flight is 5s and the horizontal range is 200m. Find the magnitude and direction of velocity of projection.
View SolutionWhat are the two angles of projection of a projectile projected with velocity of 30m/s, so that the horizontal range is 45m. Take, g=10m/s2.
View SolutionA particle is projected with a velocity of 30m/s at an angle 60∘ above the horizontal on a slope of inclination 30∘. Find its range, time of flight and angle of hit.
View SolutionA projectile is thrown with a velocity of 20 m/s, at an angle of 60∘ with the horizontal. After how much time the velocity vector will make an angle of 45∘ with the horizontal (in upward direction) is (take g=10m/s2)−
View SolutionA projectile is thrown with velocity u making an angle θ with the horizontal. Its time of flight on the horizontal ground is 4 second. The projectile is moving at angle of 45∘ with the horizontal just one second after the projection. Hence the angle θ is (take g=10m/s2)
View Solution
