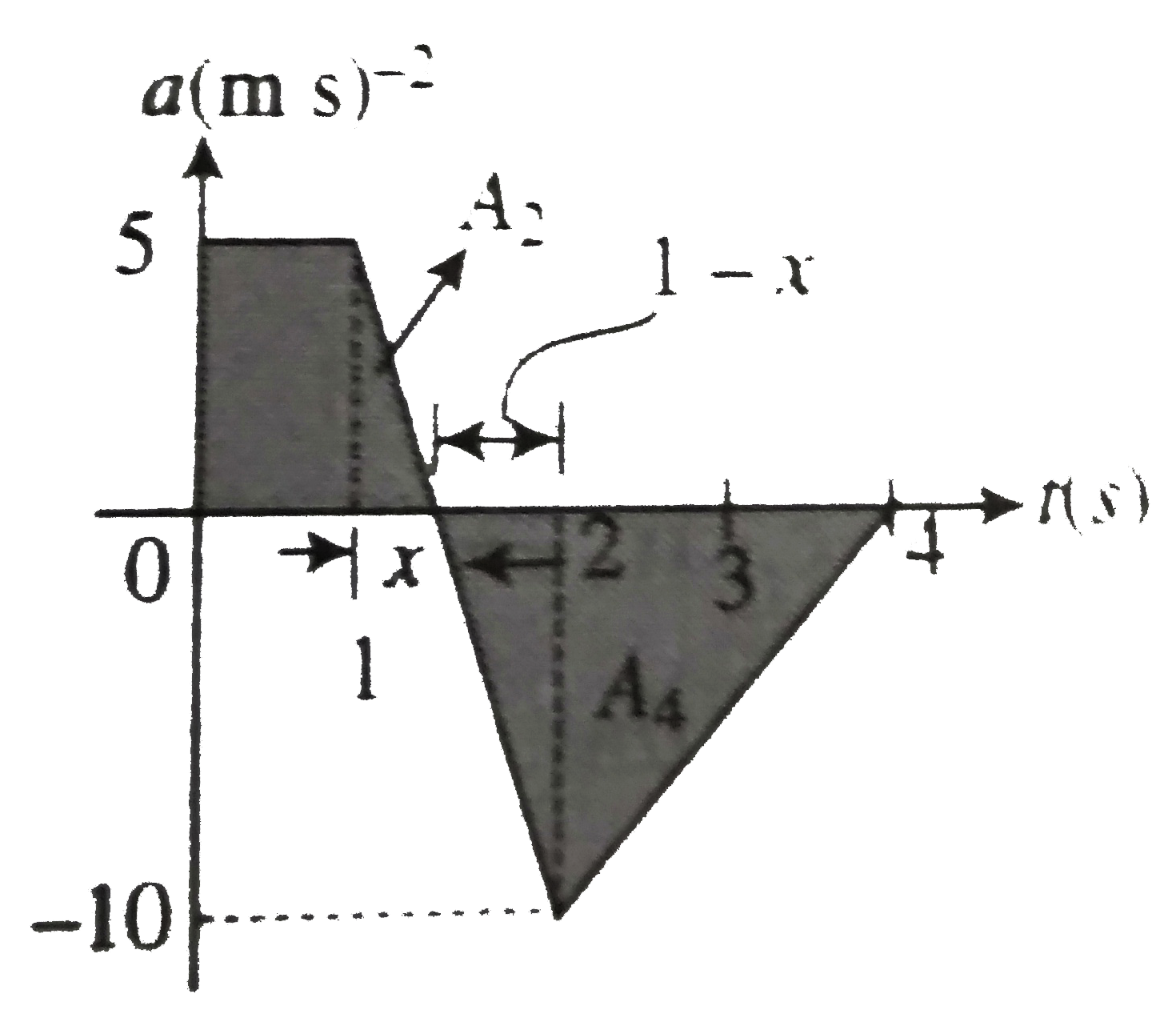
A particle moves vertically with an upwards initial speed v0=10.5ms−1. If its acceleration varies with time as shown in a-t graph in figure, find the velocity of the particles at t = 4s.

The correct Answer is:3
The velocity of the particle at
t = 4 s can be given as
→v4=→v0+Δ→v ……..(i)
where Δ→v≡A(= area under a-t
graph during first 4 s)
Referring to a -t graph (shown in
figure), we have
A=A1+A2−A3−A4
where
A1=5×1=5,A2=12×x×5
A3=12×(1−x)×10andA4=12×2×10=10
We can find the value of x as follows:
Using properties of similar triangles, we have x5=1−x10.
This yields x=13
Substituting x=13inA2=12×x×5andA3=12(1−x)×
10, we have A2=5/6and A3=10/3.
Then substituting A1,A2,A3and A4 in Eq. (ii), we have
A=−7.5⇒Δv=−7.5and→v0=10.5ms−1.
hence, we have v4=v0+Δv=10.5−7.5=3ms−1.
Topper's Solved these Questions
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Fill in the blanks
4 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - True or False
2 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Linked Comprehension Type
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
A particle moves aling x-axis with an initial speed v0=5ms−1. If its acceleration varies with with time asshown in a−t graph in .
 .
.
a. Find the time when the particle starts moving along - x direction
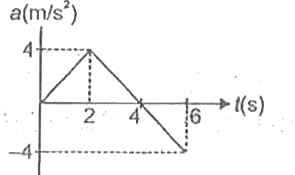
View SolutionFor the acceleration - time (a - t) graph shown in figure, the change in velocity of particle from t = 0 to t = 6 s is
View SolutionIf acceleration a(t)=3t2 and initial velocity u=0 m/s , then the velocity of the particle after time t=4 s
View SolutionA graph of acceleration versus time of a particle starting from rest at t=0 is as shown in figure. The speed of the particle at t=14s is

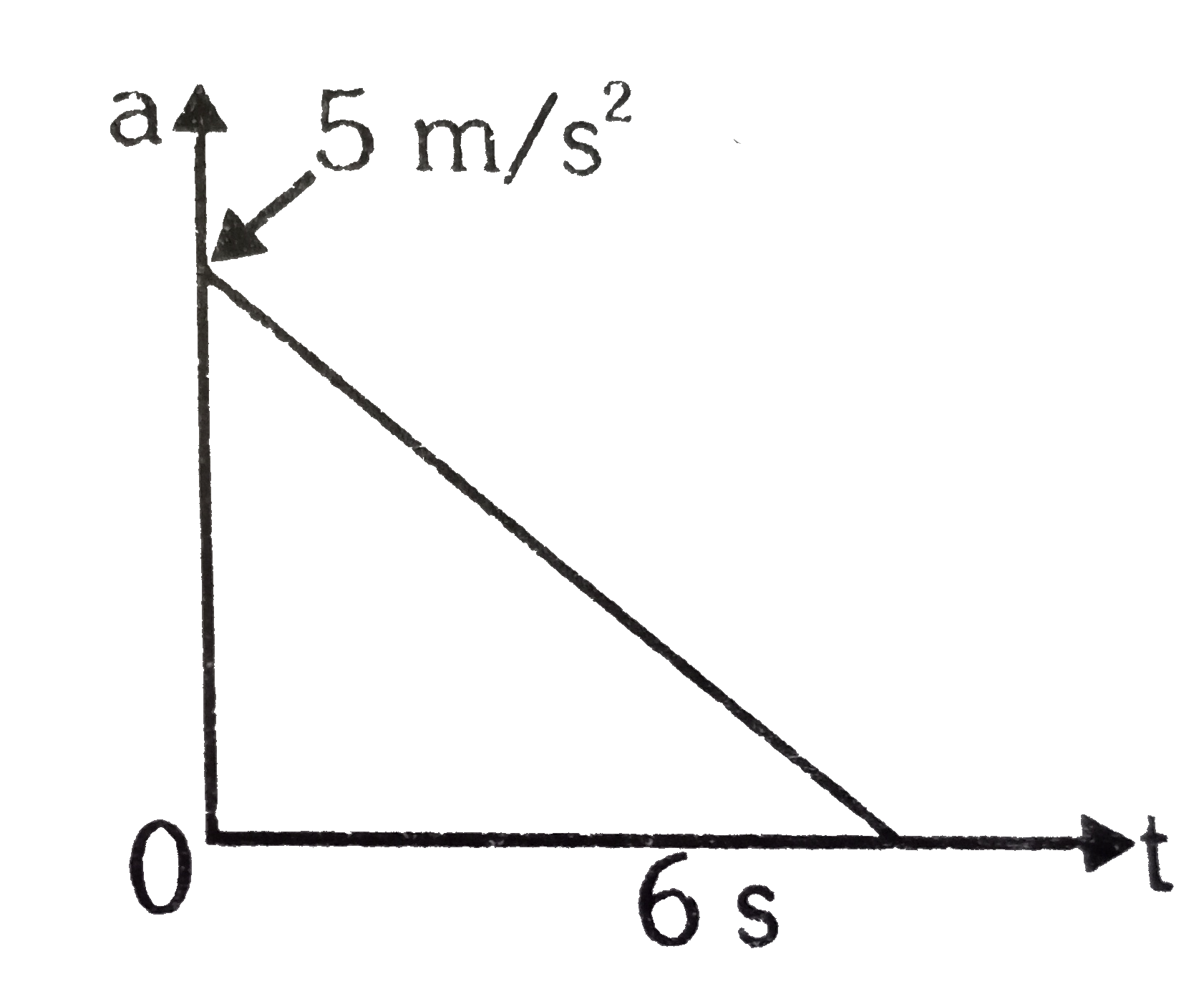
View SolutionA particle starts from rest. Its acceleration at time t=0 is 5m/s2 which varies with time as shown in the figure. The maximum speed of the particle will be
View SolutionA particle starting from rest. Its acceleration (a) versus time (t) is as shown in the figure.
The maximum speed of the particle will be.
View SolutionA particle starting from rest. Its acceleration (a) versus time (t) is as shown in the figure.
The maximum speed of the particle will be.

View SolutionThe acceleration of paticle varies with time as :
a(t)=3t2+4
If the initial velocity of particle is 2m/s, find the velocity of particle at t=3sec.
View SolutionIf a particle starts moving with initial velocity u=1ms−1 and acceleration a=2ms−2, the veloctiy of the particle at any time is given by v=u+at=1+2t. Plot the velocity-time graph of the particle.
View SolutionA particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?

View Solution
