A particle moving with uniform acceleration has average velocities ν1,ν2 and ν3 over the successive intervals of time t1,t2 and t3 respectively. The value of ν1−ν2ν2−ν3 will be
(υ1−υ2):(υ2−υ3)=(t1−t2):(t2+t3)
(υ1−υ2):(υ2−υ3)=(t1+t2):(t2+t3)
(iψlon1−υ2):(υ2−υ3)=(t1−t2):(t1−t3)
(υ1−υ2):(υ2−υ2−υ3)=(t1−t2):(t2−t3)
The correct Answer is:B
Average velocity in uniformly accelerated motion is given by,
υav=st=ut+12at2t=u+12at
Now, υ1=u+12at1,υ2=(u+at1)+12at2
and υ3=u+a(t1+t2)+12at3
∴υ1−υ2:υ2−υ3=(t1+t2):(t2+t3)
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Assertion and reason)19videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Mathch the columns)6videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.715videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrances gallery19videos
MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective10videos
PROJECTILE MOTION
Similar Questions
A particle moving with uniform acceleration has average velocities ν1,ν2 and ν3 over the successive intervals of time t1,t2 and t3 respectively. The value of ν1−ν2ν2−ν3 will be
View SolutionA particle moves in a straight line with uniform acceleration. Its velocity at time t=0 is v1 and at time t=t is v2. The average velocity of the particle in this time interval is v1+v22 . Is this statement true or false?
View Solution
Knowledge Check
- Question 1 - Select One
A point moves with a uniform acceleration and v1,v2,v3 denote the average velociies in the three succellive intervals of time t1 ,t2 and t3. Find the ratio of ( v1 - v2) and ( v2 - v3).
At1−t2t2−t3Bt1−t3t2+t3Ct1+t2t2−t3Dt1+t2t2+t3
A body is moving with variable acceleartion (a) along a straight line. The average acceleration of body in time interval t1 to t2 is :-
View SolutionA particle moves rectilinearly possessing a parabolic s-t graph. Find the average velocity of the particle over a time interval from t=12s→t=1.5s.
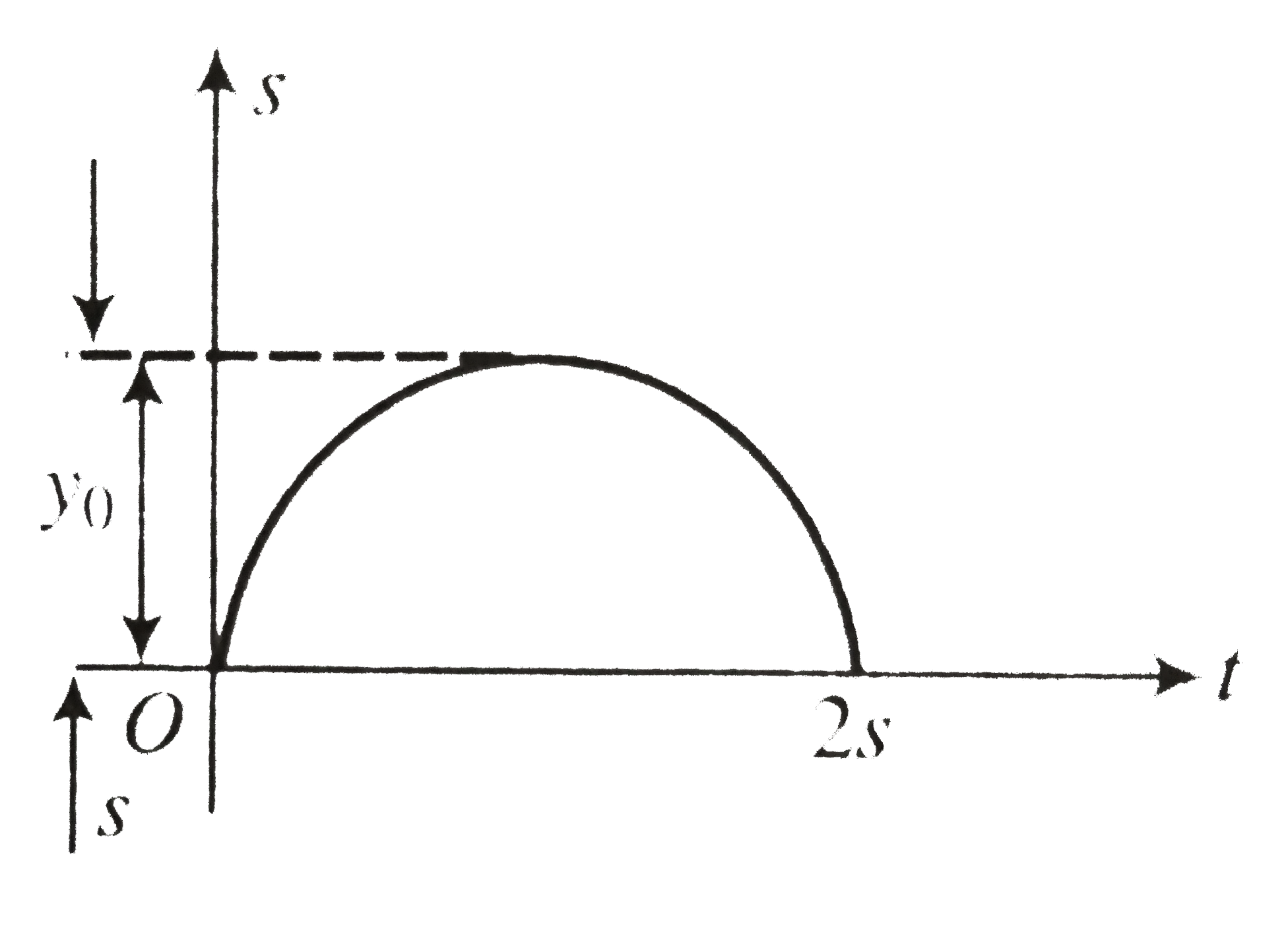 View Solution
View SolutionA particle moves in a straight line with uniform acceleration. Its velocity at time t=0 is v1 and at time t=t is v2. The average velocity of the particle in this time interval is v1+v22 . Is this statement true or false?
View SolutionPosition of a particle at any instant is given by x=3t2+1 , where x is in m and t in sec. Its average velocity in the time interval t=2 sec to t=3 sec will be :
View SolutionFind the average velocity for the time intervals Δt=t2−0.75 when t2 is 1.75 ,1.25 and 1.0 s. What is the instantaneous velocity at t=0.75 s?
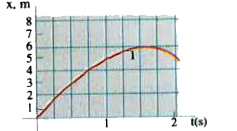 View Solution
View SolutionA particle is describing uniform circular motion in the anti-clockwise sense such that its time period of revolution is T. At t = 0 the particle is observed to be at A. If θ1 be the angle
between acceleration vector at t=T4 and average velocity vector in the time interval 0 to T/4 and θ2 be the angle between acceleration vector at t=T4 and the vector representing change in velocity in the time interval 0 to T/4, then :
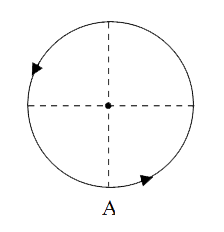 View Solution
View SolutionA particle move with velocity v1 for time t1andv2 for time t2 along a straight line. The magntidue of its average acceleration is
View Solution
