A particle starts with an initial velocity and passes successively over the two halves of a given distance with constant accelerations a1anda2 respectively. Show that the final velocity is the same as if the whole distance is covered with a uniform acceleration a1+a22.
In the first case,
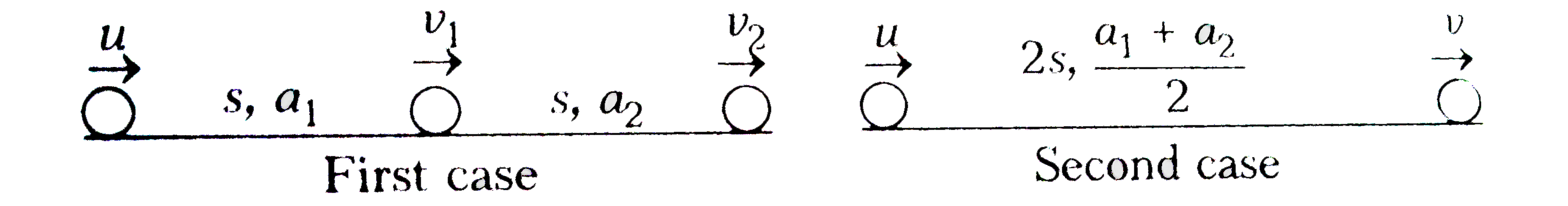
v21=u2+2a1s …..(i)
v22=v21+2a2s ….(ii)
Adding Eqs. (i) and (ii), we have
v22=u2+2(a1+a22)(2s) ….(iii)
In the second case
v2=u2+2(a1+a22)(2s) ...(iv)
From Eqs. (iii) and (iv) we can see that
v2=v
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.1
10 Videos
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.2
10 Videos
- MOTIONBOOK - DC PANDEYCHAPTER - MOTIONEXERCISE - Medical entrances gallery
19 Videos
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
Similar Questions
Knowledge Check
Starting from rest a particle is first accelerated for time t1 with constant acceleration a1 and then stops in time t2 with constant retardation a2. Let v1 be the average velocity in this case and s1 the total displacement. In the second case it is accelerating for the same time t1 with constant acceleration 2a1 and come to rest with constant retardation a2 in time t3. If v2 is the average velocity in this case and s2 the total displacement, then
Av2=2v1B2v1<v2<4v1Cs2=2s1D2s1<s2<4s1A and B participate in a race with acceleration a1anda2 , respectively . A reaches t times earlier than B at finish line and their velocities at finish line are v1andv2 , respectively. If difference between their velocities is v , then find the value of v
Aa1+a22tB√a1a2tCa1a2a1+a2tD2a1a2a1+a2tA body A starts from rest with an acceleration a1. After 2 seconds, another body B starts from rest with an acceleration a2. If they travel equal distances in the 5th second, after the start of A, then the ratio a1:a2 is equal to :
A5:9B5:7C9:5D9:7
In a car race, car A takes a time t less than car B at the finish and passes the finishing point with speed v more than that of the car B. Assuming that both the cars start from rest and travel with constant acceleration a1anda2 respectively. Show that v=√a1a2t.
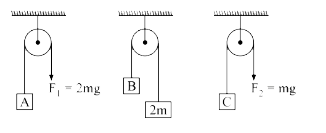
View SolutionIn the figure, blocks A, B and C of mass m each have acceleration a1, a2 and a3 respectively. F1 and F2 are external forces of magnitudes 2mg and mg respectively, then :
View SolutionIn a car race, car A takes t0 time less to finish than car B and passes the finishing point with a velocity v0 more than car B. The cars start from rest and travel with constant accelerations a1anda2. Then the ratio v0t0 is equal to.
View SolutionA body A starts from rest with an acceleration a1. After 2 seconds, another body B starts from rest with an acceleration a2. If they travel equal distances in the 5th second, after the start of A, then the ratio a1:a2 is equal to :
View SolutionA particle moves along x axis in such a way that its coordinate x varies with time t according to the equation x=A0−A1t+A2t2. The initial velocity of the particle is.
View Solution
