A pendulum has time period T in air when it is made to oscillate in water it acquired a time period T=√2T The density of the pendulum bob is equal to (density) of water =1)
√2
2
2√2
none of these
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Understand the time period of a pendulum
The time period T of a simple pendulum in air is given by the formula:
T=2π√Lg
where L is the length of the pendulum and g is the acceleration due to gravity.
Step 2: Time period in water
When the pendulum is oscillating in water, the effective acceleration due to gravity g′ is modified due to the buoyant force acting on the pendulum bob. The modified acceleration is given by:
g′=g(1−σρ)
where σ is the density of the fluid (water in this case) and ρ is the density of the pendulum bob.
Step 3: Write the time period in water
The time period T′ of the pendulum in water can be expressed as:
T′=2π√Lg′
Step 4: Relate the time periods
According to the problem, the time period in water is given by:
T′=√2T
Step 5: Set up the equation
Using the expressions for T and T′, we can set up the equation:
√2T=2π
⎷Lg(1−σρ)
Substituting T:
√2⋅2π√Lg=2π
⎷Lg(1−σρ)
Step 6: Simplify the equation
Cancel 2π√L from both sides:
√2⋅1√g=1√g(1−σρ)
Step 7: Square both sides
Squaring both sides gives:
2⋅1g=1g(1−σρ)
Step 8: Cross-multiply
Cross-multiplying leads to:
2(1−σρ)=1
Step 9: Solve for density ratio
This simplifies to:
2−2σρ=1
2σρ=1
ρ=2σ
Step 10: Substitute the value of σ
Given that the density of water σ=1:
ρ=2⋅1=2
Conclusion
The density of the pendulum bob is ρ=2.
---
The time period T of a simple pendulum in air is given by the formula:
T=2π√Lg
where L is the length of the pendulum and g is the acceleration due to gravity.
When the pendulum is oscillating in water, the effective acceleration due to gravity g′ is modified due to the buoyant force acting on the pendulum bob. The modified acceleration is given by:
g′=g(1−σρ)
where σ is the density of the fluid (water in this case) and ρ is the density of the pendulum bob.
The time period T′ of the pendulum in water can be expressed as:
T′=2π√Lg′
According to the problem, the time period in water is given by:
T′=√2T
Using the expressions for T and T′, we can set up the equation:
√2T=2π
⎷Lg(1−σρ)
Substituting T:
√2⋅2π√Lg=2π
⎷Lg(1−σρ)
Cancel 2π√L from both sides:
√2⋅1√g=1√g(1−σρ)
Squaring both sides gives:
2⋅1g=1g(1−σρ)
Cross-multiplying leads to:
2(1−σρ)=1
This simplifies to:
2−2σρ=1
2σρ=1
ρ=2σ
Given that the density of water σ=1:
ρ=2⋅1=2
The density of the pendulum bob is ρ=2.
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective type
3 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A simple pendulum has a time period T in vacuum. Its time period when it is completely immersed in a liquid of density one-eight of the density of material of the bob is
View SolutionA simple pendulum has some time period T. What will be the percentage change in its time period if its amplitude is decreased by 5%
View SolutionA pendulum has time period T for small oscillations. An obstacle P is situated below the point of suspension O at a distance 3l4. The pendulum is released from rest. Throughout the motion, the moving string makes small angle with vertical. Time after which the pendulum returns back to its initial position is
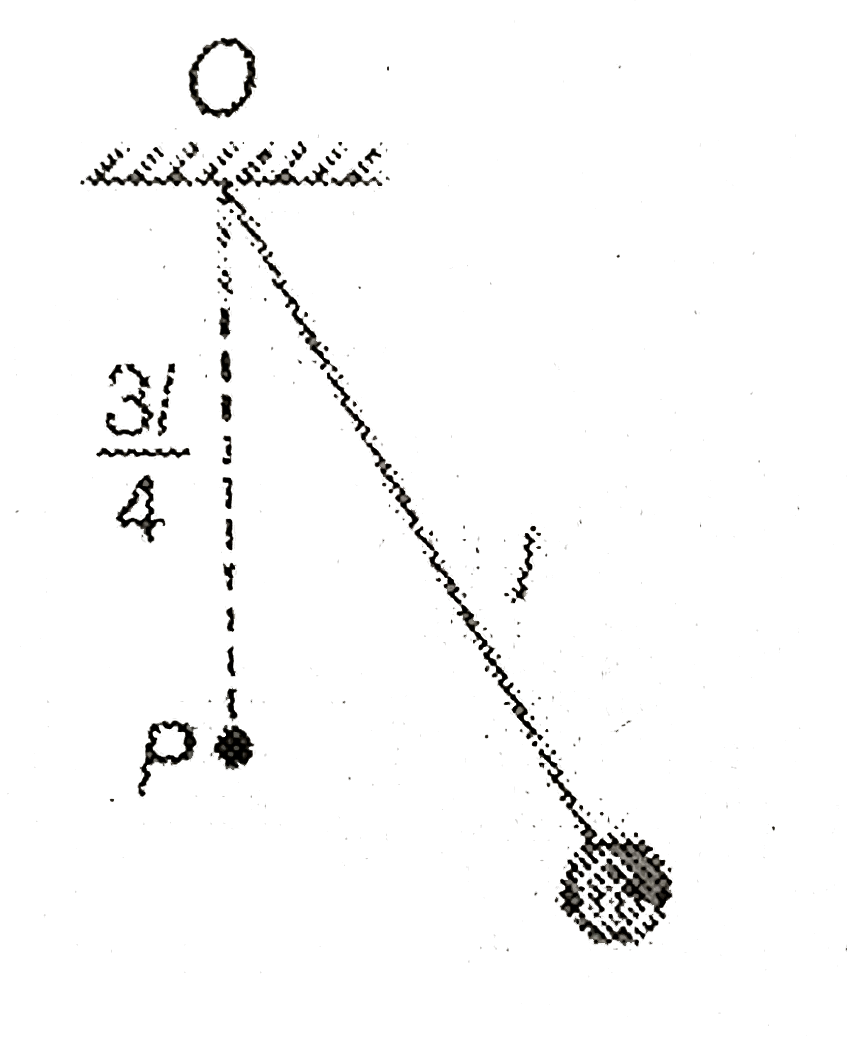
View SolutionA simple pendulum has time period T = 2s in air. If the whole arrangement is placed in a non viscous liquid whose density is 1/2 times the density of bob. The time period in the liquid will be
View SolutionA simple pendulum has time period T The bob is given negative charge and surface below it is given positive change new time period will be
View SolutionIn a simple pendulum the period of oscillation (T) is related to the length of the pendulum (L) as
View SolutionA pendulum is suspended in a lit and its period of oscillation is T0 when the lift is stationary.
(i) What will be the period T of oscillation of pendulum, if the lift begins to accelerates downwards with an acceleration equal to 3g4 ?
View SolutionThe graph between time period (T) and length (l) of a simple pendulum is
View SolutionA simple pendulum with a solid metal bob has a period T. What will be the period of the same pendulum if it is made to oscillate in a non - viscous liquid of density one - tenth of the of the metal of the bob ?
View SolutionA pendulum is suspended in a ligt and its period of oscillation when the lift is stationary is Ta. What must be the accleraion of the lift for the period of oscillation of the pendulum to be T0/2?
View Solution
