A person is looking at the flat surface of a transparent hemispher of refractive index μ−√2 . Half of the flat surface is coloured black and half of curved surface is coloured in six equally spaced strips as shown in Figure. Then
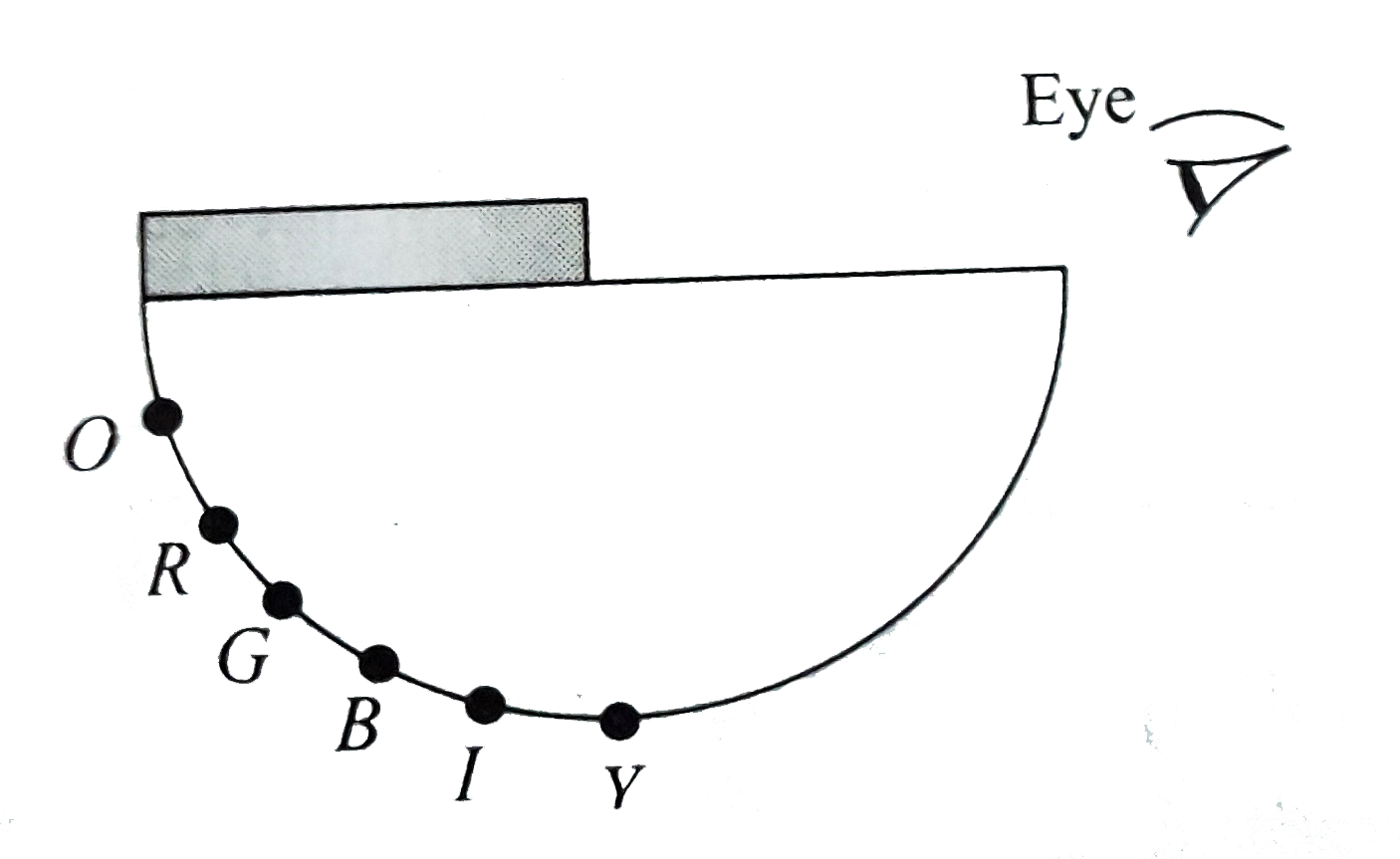
the person can see green, orange and red
the person can see only yellow, indigo and blue
the ray coming from red and organge strips will be totally reflected
the ray coming from yellow, indigo and blue stips will be totally reflected
The correct Answer is:b.,c.
Let C be the critical angle: sinC=1μ=1√2
C=45∘
For Y,I and B, angle of incidence at a point on QP can be less than C, so they will be refracted from QP and can be seen by person
But for G,R and O, angle of incidence at a point on QP will be more than C. Hence, they will be internally reflected.

Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK
1 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
Similar Questions
A parallel beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index 2.0 as shown in figure. The position of the image formed by refraction at the first surface is :

View SolutionA ray of light is incident on the surface of a transparent sphere of R.I.μ=√72. After refraction is is internally reflected and refracted out of the sphere as shown in the figure. Find the angle of incidence 'I' so that the total deviation produced is minimum. 'C' is the centre of the sphere.
 .
.
View Solution
Knowledge Check
A parallel narrow beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index μ=1.5 as shown. The position of the image formed by refraction at the image formed by refraction at the spherical surface only as
 AR2B3RCR3D2R
AR2B3RCR3D2RA ray of light is incident on the surface of a sphere of refractive index √72 other half of sphere is silvered. After refraction it is reflected and then refracted out of sphere again such that the total deviation is minimum then total deviation of the ray will be (sin410−√37)
 A1020B980C1360D1630
A1020B980C1360D1630Find the distance of object placed in the slab of refractive index μ from point P of the curved surface of radius R so that image is formed at infinity:
 A(μ−1)RμBμR(μ−1)CR(μ−1)D(μ−1)R2μ
A(μ−1)RμBμR(μ−1)CR(μ−1)D(μ−1)R2μ

A right angled triangular prism of refractive index μ1 is kept floating on a liquid (surface) having refractive index μ2. The condition such tat light incident normally passes through base of prism as shown in figure.
View SolutionLight ray is incident on a prism of angle A=60∘and refractive indexμ=√2.the angle of incidence at which the emergent ray grazes the surface is given by
View SolutionLight ray is incident on a prism of angle A=60∘ are refractive index μ=√2. The angle of incidence which the emergent rays grazes the surface is given
View SolutionHalf the surface of a transparent sphere of refractive index 2 is silvered. A narrow, paralel beam of light is incident on the unsilvered surface, symmetrically with respect to the silvered part. The light finally emerging from theh sphere will be a
View SolutionHalf the surface of a transparent sphere of refractive index 2 is silvered. A narrow, parallel beam of light is incident on the unsilvered surface, symmetrically with respect to the silvered part. The light finally emerging from the sphere will be a
View Solution
