A pipe of non uniform cross section has two distinct section 1 and 2 with areas 2cm2 and 4cm2 respectively. If the velocity of flowing liquid at section 1 is 5cm/s, determine the velocity at section 2.
To solve the problem of determining the velocity at section 2 of a pipe with non-uniform cross-section, we can use the principle of conservation of mass, which is represented by the continuity equation. Here’s a step-by-step solution:
Step 1: Identify the given values
- Cross-sectional area at section 1, A1=2cm2
- Cross-sectional area at section 2, A2=4cm2
- Velocity at section 1, V1=5cm/s
Step 2: Write the continuity equation
The continuity equation states that the product of the cross-sectional area and the velocity at any two points in a fluid flow must be equal. Mathematically, it is expressed as:
A1V1=A2V2
Step 3: Substitute the known values into the equation
Substituting the known values into the continuity equation:
2cm2×5cm/s=4cm2×V2
Step 4: Solve for V2
Now we can solve for V2:
10cm3/s=4cm2×V2
V2=10cm3/s4cm2=104cm/s=2.5cm/s
Step 5: Conclusion
Thus, the velocity at section 2, V2, is 2.5cm/s.
---
- Cross-sectional area at section 1, A1=2cm2
- Cross-sectional area at section 2, A2=4cm2
- Velocity at section 1, V1=5cm/s
The continuity equation states that the product of the cross-sectional area and the velocity at any two points in a fluid flow must be equal. Mathematically, it is expressed as:
A1V1=A2V2
Substituting the known values into the continuity equation:
2cm2×5cm/s=4cm2×V2
Now we can solve for V2:
10cm3/s=4cm2×V2
V2=10cm3/s4cm2=104cm/s=2.5cm/s
Thus, the velocity at section 2, V2, is 2.5cm/s.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples
7 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.1
11 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A horizontal pipe of varying cross-sectional area carries water flowing at a constant rate. The pressure at sections (1) and (2) are 50cm and 20cm of Hg. If the velocity of section (1) is 5m/s, what is the velocity of section (2). Also determine the ratio of areas at sections (1) and (2) (as shown in Fig.
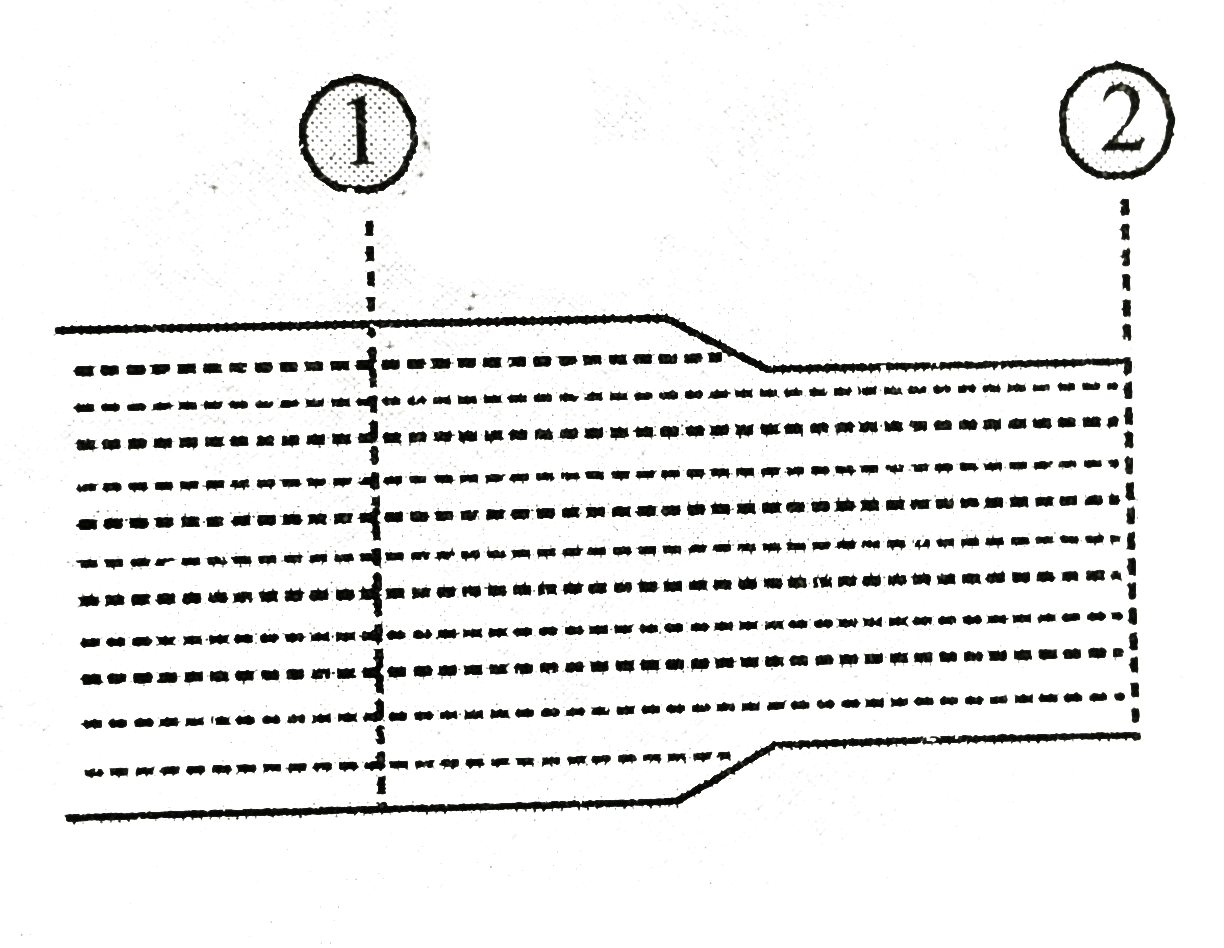
View SolutionThe area of cross-section of a current carrying conductor is A∘ and A∘4 at section (1) and (2) respectively If V1.V2 and E1.E2 be the drift velocity and electric field at section 1 and 2 respectively then
View Solution
Knowledge Check
An ideal fluid flows through a pipe of circular cross-section made of two sections with diameters 2.5cm and 3.75cm. The ratio of the velocities in the two pipes is
A9:4B3:2C√3:√2D√2:√3An ideal fluid flows through a pipe of circular cross-section made of two sections with diameters 2.5cm and 3.75cm. The ratio of the velocities in the two pipes is
A9:4B3:2C√3:√2D√2:√3
An ideal fluid flows through a pipe of circular cross-section made of two sections with diameters 2.5cm and 3.75cm. The ratio of the velocities in the two pipes is
View SolutionWater is flowing steadily through a horizontal pipe of non - uniform cross - section . If the velocity of water cross - section is 0.02m2 is 2m/s , what is the velocity of water at another point where the cross - section is 0.01m2 ?
View SolutionA liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross section A1 and A2 are v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h. Then

View SolutionWater flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are 5cm2and2cm2 respectively. The rate of flow of water through the tube is 500cm3s−1 . Find the difference of mercury levels in the U-tube.

View SolutionWater flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are 5cm2and2cm2 respectively. The rate of flow of water through the tube is 500cm3s−1 . Find the difference of mercury levels in the U-tube.

View SolutionWater flows through a horizontal tube as shown in figure. If the difference of height of water column in the vertical tubes in 2cm and the areas of corss-section at A and B are 4cm2 and 2cm2 respectively. Find the rate of flow of water across any section.
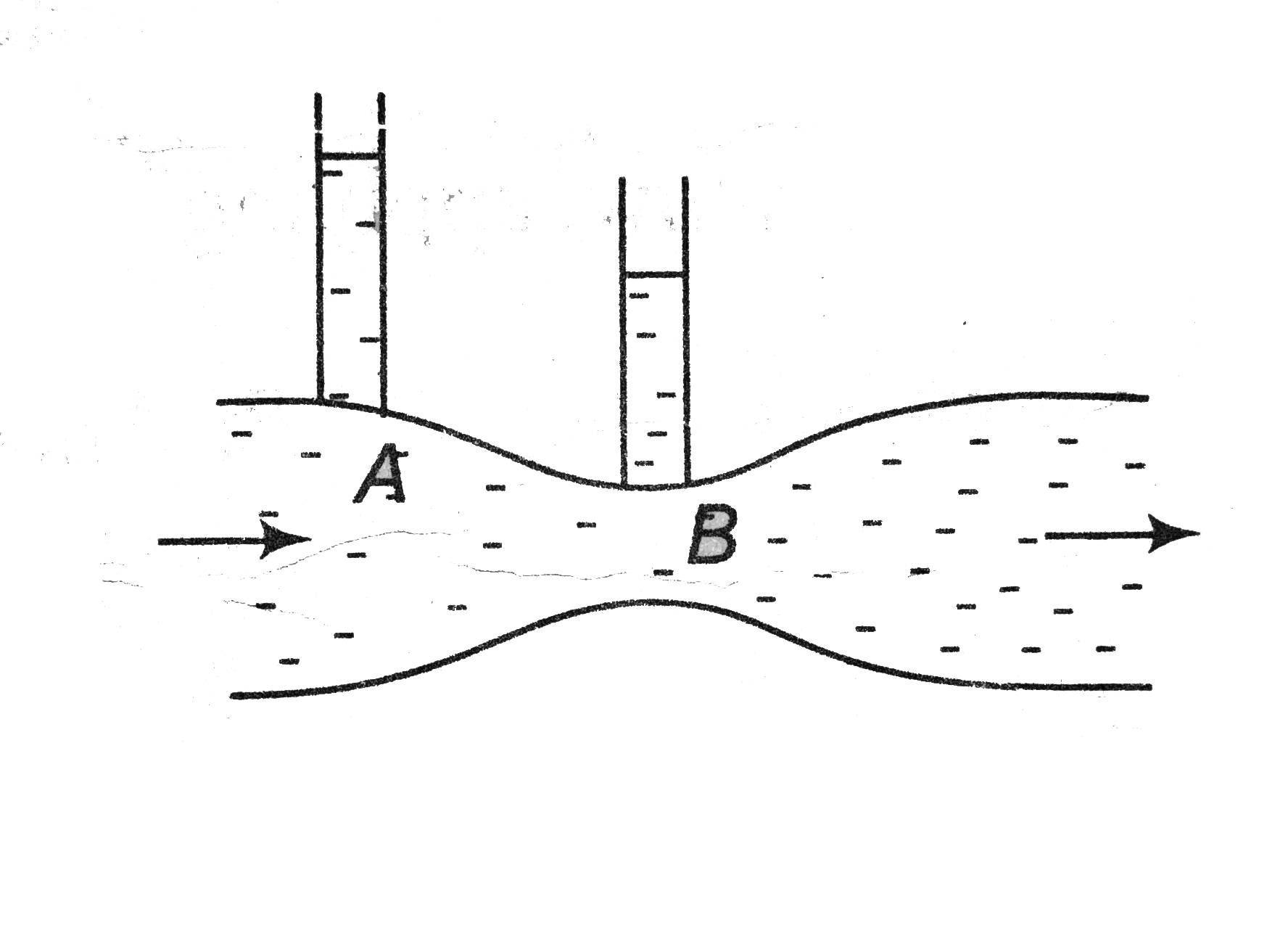 .
.
View Solution

