A planar coil having 12 turns carries 15 A current. The coil is oriented with respect to the uniform magnetic field B=0.2ˆiT such that its directed area is A=0.04ˆim2. the potential energy of the coil in the given orientation is
0
+0.72J
+1.44J
−1.44J
The correct Answer is:d
To find the potential energy of the coil in the given magnetic field, we can follow these steps:
Step 1: Identify the given values
- Number of turns (N) = 12
- Current (I) = 15 A
- Area (A) = 0.04 m²
- Magnetic field (B) = 0.2 T
Step 2: Calculate the magnetic moment (m)
The magnetic moment (m) of the coil can be calculated using the formula:
m=N⋅I⋅A
Substituting the values:
m=12⋅15⋅0.04
Step 3: Perform the multiplication
Calculating the above expression:
m=12⋅15=180
m=180⋅0.04=7.2A m2
Step 4: Calculate the potential energy (U)
The potential energy (U) of the coil in the magnetic field is given by the formula:
U=−m⋅B⋅cos(θ)
Since the coil is oriented such that the area vector is in the same direction as the magnetic field, the angle θ=0∘. Thus, cos(0)=1.
So, the formula simplifies to:
U=−m⋅B
Step 5: Substitute the values into the potential energy formula
Substituting the values we have:
U=−7.2⋅0.2
Step 6: Calculate the potential energy
Calculating the above expression:
U=−1.44J
Final Answer
The potential energy of the coil in the given orientation is:
U=−1.44J
---
- Number of turns (N) = 12
- Current (I) = 15 A
- Area (A) = 0.04 m²
- Magnetic field (B) = 0.2 T
The magnetic moment (m) of the coil can be calculated using the formula:
m=N⋅I⋅A
Substituting the values:
m=12⋅15⋅0.04
Calculating the above expression:
m=12⋅15=180
m=180⋅0.04=7.2A m2
The potential energy (U) of the coil in the magnetic field is given by the formula:
U=−m⋅B⋅cos(θ)
Since the coil is oriented such that the area vector is in the same direction as the magnetic field, the angle θ=0∘. Thus, cos(0)=1.
So, the formula simplifies to:
U=−m⋅B
Substituting the values we have:
U=−7.2⋅0.2
Calculating the above expression:
U=−1.44J
The potential energy of the coil in the given orientation is:
U=−1.44J
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Match the following
4 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
Similar Questions
A planar coil having 15turns carries 20 A currennt . The coil is oriented with respect to the unifrom magnetic field B = 0.5 T such that its direction area is A=−0.04ˆim2. The potenial energy of the coil in the given orientation is
View SolutionA current carrying coil is subjected to a uniform magnetic field. The coil will orient so that its plane become
View Solution
Knowledge Check
A circular coil of radius 10 cm having 100 turns carries a current of 3.2 A. The magnetic field at the center of the coil is
A2.01×10−3TB5.64×10−3TC2.64×10−3TD5.64×10−3T
A current carrying coil is subjected to a uniform magnetic field. The coil will orient so that its plane become
View SolutionA coil having N turns carry a current I as shown in the figure. The magnetic field intensity at point P is
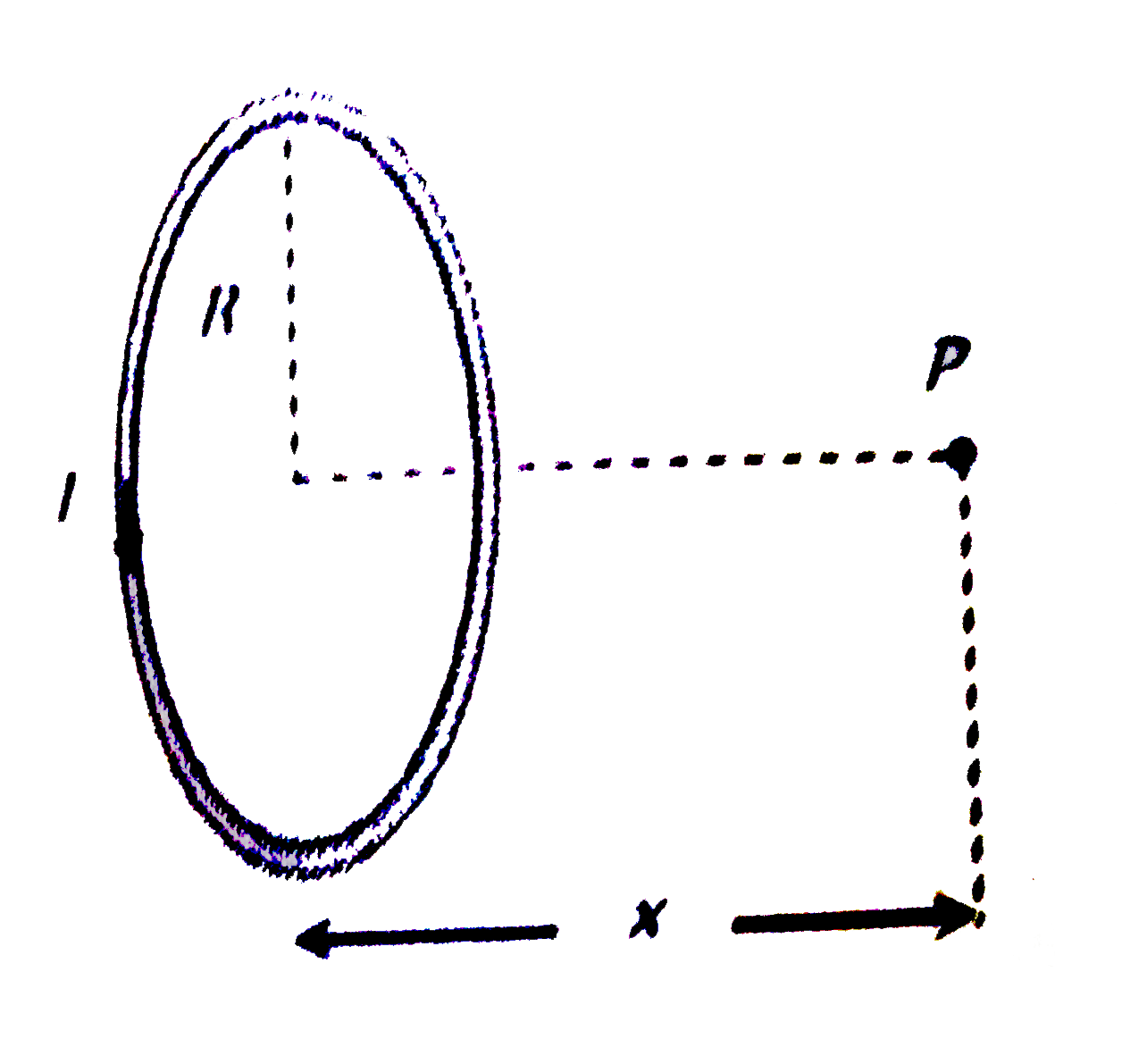
View SolutionA circular coil having N turns and radius r carries a current I. It is held in the XZ plane in a magnetic field Bˆi. The torque on the coil due to the magnetic field is :
View SolutionA circular coil having N turns and radius r carries a current I. It is held in the XZ plane in a magnetic field Bˆi. The torque on the coil due to the magnetic field is :
View SolutionA rectangular coil 20cm×20cm has 100 turns and carries a current of 1A. It is placed in a uniform magnetic field B=0.5T with the direction of magnetic field parallel to the plane of the coil. The magnitude of the torque required to hold this coil in this position is
View SolutionA rectangular coil 20cm×20cm has 100 turns and carries a current of 1A. It is placed in a uniform magnetic field B=0.5T with the direction of magnetic field parallel to the plane of the coil. The magnitude of the torque required to hold this coil in this position is
View SolutionA small circular coil with a mass of m consists of N turns of fine wire and carries a current of I. The coil is located in a uniform magnetic field of B with the coil axis orginally parallel to the field direction.

a. What is the period of small angle oscilations of the coil axis around its equilibrium position, assuming no friction and no mechanical force?
b. If the coil is rotated through an angle of θ from its equilibrium position and then released, what will be its angular speed when it passes through equilibrium position?
View Solution
