A plane EM wave travelling along z direction is described by
E=E0sin(kz−ωt)ˆiandB=B0sin(kz−ωt)ˆj.
show that
(i) The average energy density of the wave is given by uav=14ε0E20+14B20μ0.
(ii) The time averaged intensity of the wave is given by Iav=12cε0E20.
To solve the problem, we need to find the average energy density and the time-averaged intensity of a plane electromagnetic wave described by the electric field E=E0sin(kz−ωt)^i and the magnetic field B=B0sin(kz−ωt)^j.
Part (i): Average Energy Density
1. Energy Density in Electric Field:
The energy density uE in the electric field is given by:
uE=12ϵ0E2
where E=E0sin(kz−ωt).
2. Average of E2:
The average value of E2 over one complete cycle is:
⟨E2⟩=⟨(E0sin(kz−ωt))2⟩=E20⟨sin2(kz−ωt)⟩
The average value of sin2 over one cycle is 12:
⟨E2⟩=E20⋅12=E202
3. Substituting into Energy Density:
Now substituting this back into the expression for uE:
uE=12ϵ0(E202)=14ϵ0E20
4. Energy Density in Magnetic Field:
The energy density uB in the magnetic field is given by:
uB=12B2μ0
where B=B0sin(kz−ωt).
5. Average of B2:
Similarly, the average value of B2 is:
⟨B2⟩=⟨(B0sin(kz−ωt))2⟩=B20⟨sin2(kz−ωt)⟩=B20⋅12=B202
6. Substituting into Energy Density:
Now substituting this back into the expression for uB:
uB=12(B202)μ0=14B20μ0
7. Total Average Energy Density:
The total average energy density uav is the sum of the electric and magnetic energy densities:
uav=uE+uB=14ϵ0E20+14B20μ0
Part (ii): Time-Averaged Intensity
1. Intensity Definition:
The intensity I of an electromagnetic wave is defined as the average power per unit area. It can be expressed in terms of the average energy density and the speed of light c:
I=cuav
2. Using the Relationship Between E0 and B0:
From electromagnetic wave theory, we know that:
c=E0B0orB0=E0c
3. Substituting B0:
Substitute B0 into the expression for uav:
uav=14ϵ0E20+14(E0c)2μ0
Since μ0=1c2ϵ0, we have:
14E20μ0=14c2ϵ0E20
4. Combining Terms:
Thus, we can write:
uav=14ϵ0E20+14ϵ0E20=12ϵ0E20
5. Calculating Intensity:
Now substituting back into the intensity formula:
Iav=cuav=c(12ϵ0E20)=12cϵ0E20
Final Results:
- (i) The average energy density is:
uav=14ϵ0E20+14B20μ0
- (ii) The time-averaged intensity is:
Iav=12cϵ0E20
The energy density uE in the electric field is given by:
uE=12ϵ0E2
where E=E0sin(kz−ωt).
The average value of E2 over one complete cycle is:
⟨E2⟩=⟨(E0sin(kz−ωt))2⟩=E20⟨sin2(kz−ωt)⟩
The average value of sin2 over one cycle is 12:
⟨E2⟩=E20⋅12=E202
Now substituting this back into the expression for uE:
uE=12ϵ0(E202)=14ϵ0E20
The energy density uB in the magnetic field is given by:
uB=12B2μ0
where B=B0sin(kz−ωt).
Similarly, the average value of B2 is:
⟨B2⟩=⟨(B0sin(kz−ωt))2⟩=B20⟨sin2(kz−ωt)⟩=B20⋅12=B202
Now substituting this back into the expression for uB:
uB=12(B202)μ0=14B20μ0
The total average energy density uav is the sum of the electric and magnetic energy densities:
uav=uE+uB=14ϵ0E20+14B20μ0
The intensity I of an electromagnetic wave is defined as the average power per unit area. It can be expressed in terms of the average energy density and the speed of light c:
I=cuav
From electromagnetic wave theory, we know that:
c=E0B0orB0=E0c
Substitute B0 into the expression for uav:
uav=14ϵ0E20+14(E0c)2μ0
Since μ0=1c2ϵ0, we have:
14E20μ0=14c2ϵ0E20
Thus, we can write:
uav=14ϵ0E20+14ϵ0E20=12ϵ0E20
Now substituting back into the intensity formula:
Iav=cuav=c(12ϵ0E20)=12cϵ0E20
- (i) The average energy density is:
uav=14ϵ0E20+14B20μ0
- (ii) The time-averaged intensity is:
Iav=12cϵ0E20
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - SHORT ANSWER7videos
ELECTROMAGNETIC WAVES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - Long11videos
ELECTROMAGNETIC INDUCTION
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Long Answer Type Question10videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
Similar Questions
An electromagnetic wave going through vacuum is described by
E=E0sin(kx−ωt),B=B0sin(kx−ωt).
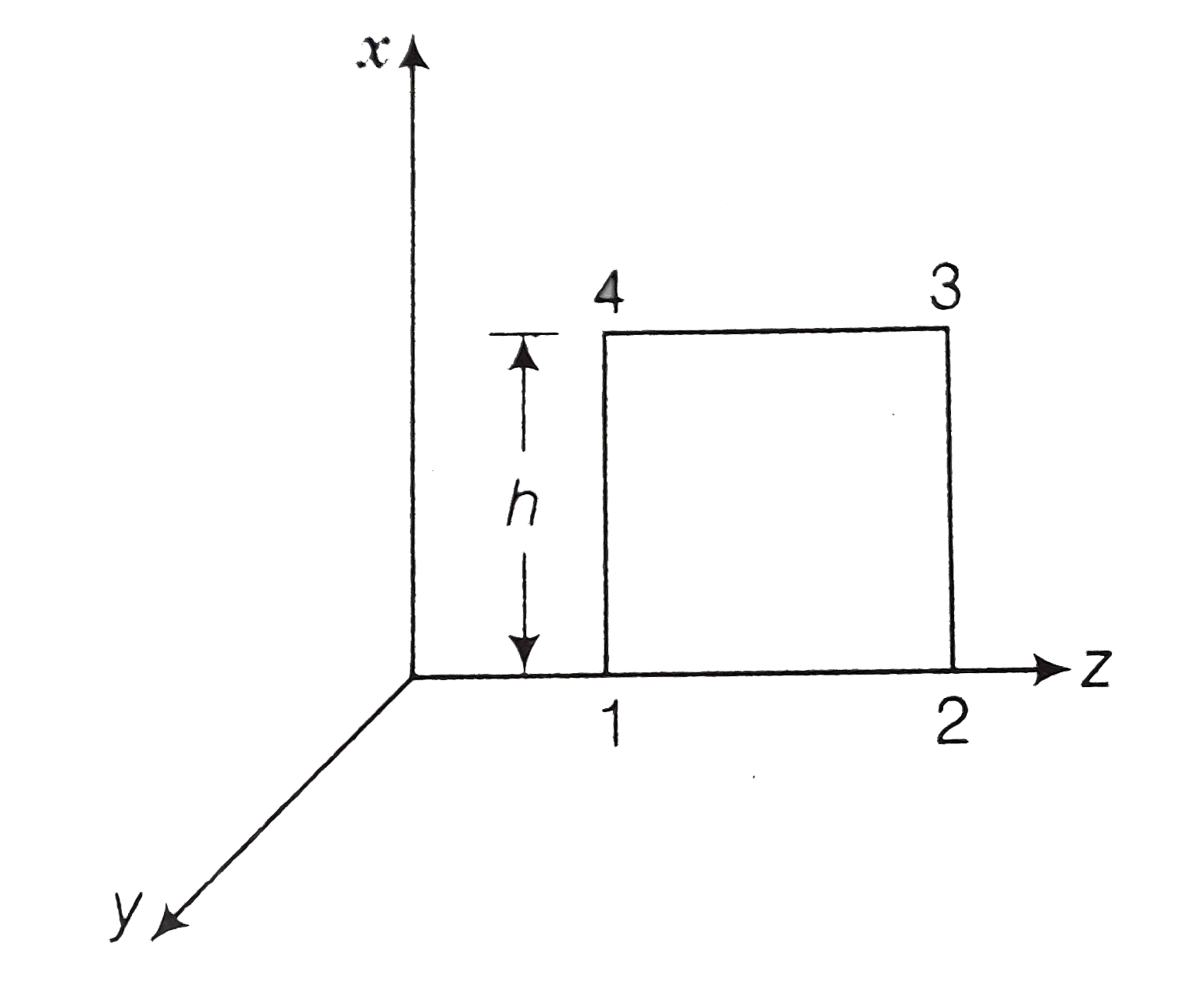
ThenView SolutionA plane EM wave travelling in vacuum along z-direction is given by E=E0 sin (kz−ωt)ˆi and B=B0 sin (kz−ωt)ˆj
(i) Evaluate ∫E.dl over the rectangular loop 1234 shown in figure.
(ii) Evaluate ∫B.ds over the surface bounded by loop 1234.
(iii) Use equation ∫E.dl=−dϕBdt to prove E0B0=c.
(iv) By using similar proces and the equation
∫B.dl=μ0I+ε0dϕEdt, prove that c1√μ0ε0
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
An electromagnetic wave travelling along z-axis is given as E=E0 cos (kz−ωt). Choose the correct options from the following
AThe associated magnetic field is given as →B=1cˆk×→E=1ω(→k×→E)BThe electromagnetic field can be written in terms of the associated magnetic field as →E=c(→B׈j)Cˆk.→E=0,ˆk.→B≠0Dˆk.→E=0,ˆk×→B=0 - Question 2 - Select One
The electric field of an electromagnetic wave travelling through vacuum is given by the equation E=E0sin(kx−ωt) The quantity that is independent of wavelength is
AkωBkωCk2ωDω
An EM wave travels in vacuum along z direction:
→E=(E1ˆi+E2ˆj)cos(kz−ωt). Choose the correct option from the following :View SolutionAn electromagnetic wave travelling along z-axis is given as E=E0 cos (kz−ωt). Choose the correct options from the following
View SolutionShow that average value of radiant flux density S over a single period 'T' is given by S=12cμ0E20.
View SolutionAn electromagnetic wave going through vacuum is described by
E=E0sin(kx−ωt). Which of the following is/are independent of the wavelength?View SolutionAn e.m. wave travels in vacuum along z direction:
→E=(E1ˆi+E2ˆj)cos(kz−ω). Choose the correct option from the following :View SolutionElectric field in EM waves is E=E0sin(kz−ωt)(ˆi+ˆj), then equation of magnetic field is:
View Solution

