A platinum resistance thermometer is constructed which reads ,00 at ice point and 1000 at steam point. Let tp denote temperature on this scale and let t denote the temperature on a mercury on a mercury thermometer scale. The resistance of the platinum coil varies with t as R1=R0(1+αt+βt2). Derive an expression for the resistance as a function of Tp.
To derive the expression for the resistance of a platinum resistance thermometer as a function of the temperature Tp on its scale, we start with the given information and relationships.
Step 1: Define the relationship between Tp and resistance RTP
We know that the temperature Tp on the platinum thermometer scale can be defined in terms of its resistance RTP as follows:
Tp=RTP−R0R100−R0×100
Where:
- RTP is the resistance at temperature Tp
- R0 is the resistance at 0°C (ice point)
- R100 is the resistance at 100°C (steam point)
Step 2: Rearranging the equation to express RTP
From the above equation, we can rearrange it to express RTP:
RTP=Tp100(R100−R0)+R0
Step 3: Substitute R100 using the resistance-temperature relationship
The resistance of the platinum coil varies with temperature t (on the mercury scale) as follows:
R100=R0(1+αt+βt2)
Substituting t=100 into this equation gives:
R100=R0(1+100α+1002β)
Step 4: Substitute R100 back into the equation for RTP
Now we substitute R100 back into the equation for RTP:
RTP=Tp100(R0(1+100α+1002β)−R0)+R0
Step 5: Simplifying the equation
This simplifies to:
RTP=Tp100(R0(100α+1002β))+R0
RTP=R0+R0Tp100(100α+1002β)
RTP=R0(1+αTp+βT2p)
Final Expression
Thus, the expression for the resistance RTP as a function of the platinum thermometer temperature Tp is:
RTP=R0(1+αTp+βT2p)
- RTP is the resistance at temperature Tp
- R0 is the resistance at 0°C (ice point)
- R100 is the resistance at 100°C (steam point)
Topper's Solved these Questions
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 1
12 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Exercise
34 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 2
6 Videos
- GRAVITATIONBOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - Question for short Answers
18 Videos
- HEAT TRANSFERBOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - QUESTIONS FOR SHORT ANSWER
11 Videos
Similar Questions
A platinum resistance thermometer reads 0∘ when its resistance is 80Ω and 100∘ when its resistance is 90Ω. Find the temperature at the platinum scale at which the resistance is 86Ω.
View SolutionA platinum resistance thermometer reads 0∘C when its resistance is 80Ωand100∘C when its resistance is 90Ω. Find the temperature at which the resistance is 86Ω.
View SolutionThe steam point and the ice point of a Mercury thermometer are marked as 800and200. What will be the temperature in centigrade mercury scale when this thermometer reads 320?
View SolutionA platinum resistance thermometer reads 00 and 1000 at the ice point and boiling point of water respectively. The resistance of a platinum wire varies with Celsius temperature θ as Rt=R0(1+αθ+βθ2), where α=3.8×10−3^0C−1 and β=−5.6×10−7^0C−2. What will be the reading of this thermometer if it is placed in a liquid bath maintained at 500C?
View SolutionA constant volume gas thermometer shows pressure readings of 60 cm and 90 cm of mercury at 0∘C and 100∘C respectively. What is the temperature on gas scale, when pressure reading is 70 cm of mercury?
View SolutionIn a platinum resistance thermometer resitance of the platinum wire at 0∘C,100∘C and in hot bath are 8Ω,12Ω and 11Ω respectively. Temperature of hot bath is
View SolutionThe resistance R of a conductor varies with temperature t as shown in the figure. If the variation is represented by Rt=R0[1+αt+βt2], then
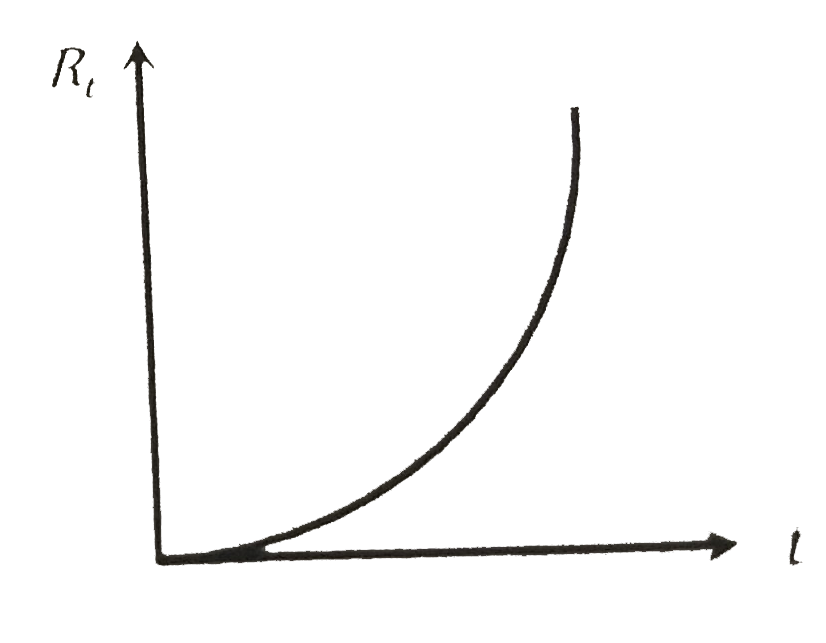
View SolutionA resistance thermometer reads R=20.0Ω,27.5Ω, and 50.0Ω at the ice point (0∘C), the steam point (100∘C) and the zinc point (420∘C) respectively. Assuming that the resistance varies with temperature as RΘ=R0(1+αΘ+βΘ2) , find the values of R0, α and β. Here Θ represents the temperature on Celsius scale.
View SolutionThe current in the inner coil is I=2t2. Find the heat developed in the outer coil between t =0 and t seconds. The resistance of the outer coil is R and take b>>a.

View SolutionResistance of a resistor at temperature t∘C is Rt=R0(1+αt+βt2), where R0 is the resistance at 0∘C. The temperature coefficient of resistance at temperature t∘C is
View Solution
