A point A is located on the rim of a wheel of radius which rolls without slipping along a horizontal surface with velocity . Find:
(a) the modulus and the direction of the acceleration vector of the point A,
(b) the total distance s traveresed by the point A between the two successive moments at which it touches the surface.
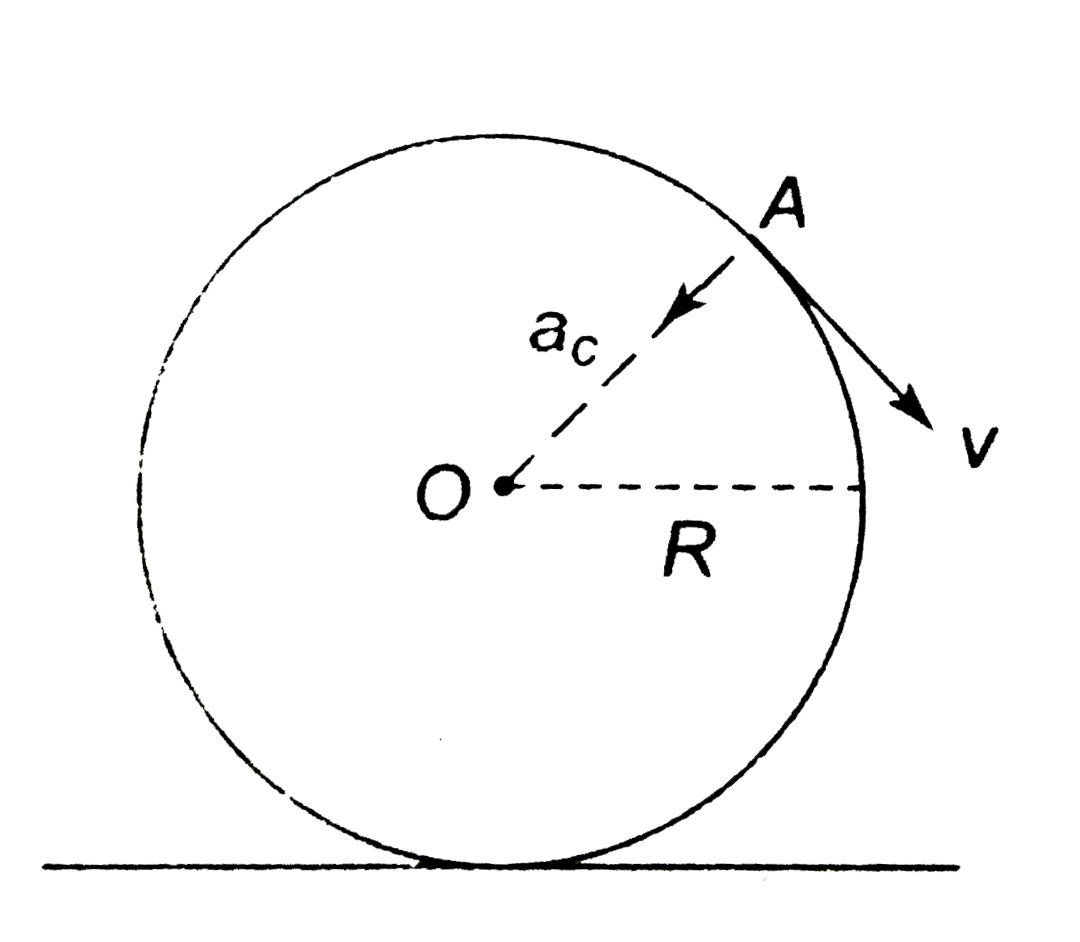
() Since the speed of wheel is constant, acceleration will be due to rotation (in the form of centripetal acceleration, because the direction of velocity is changing)
, always directed towards the center of wheel.
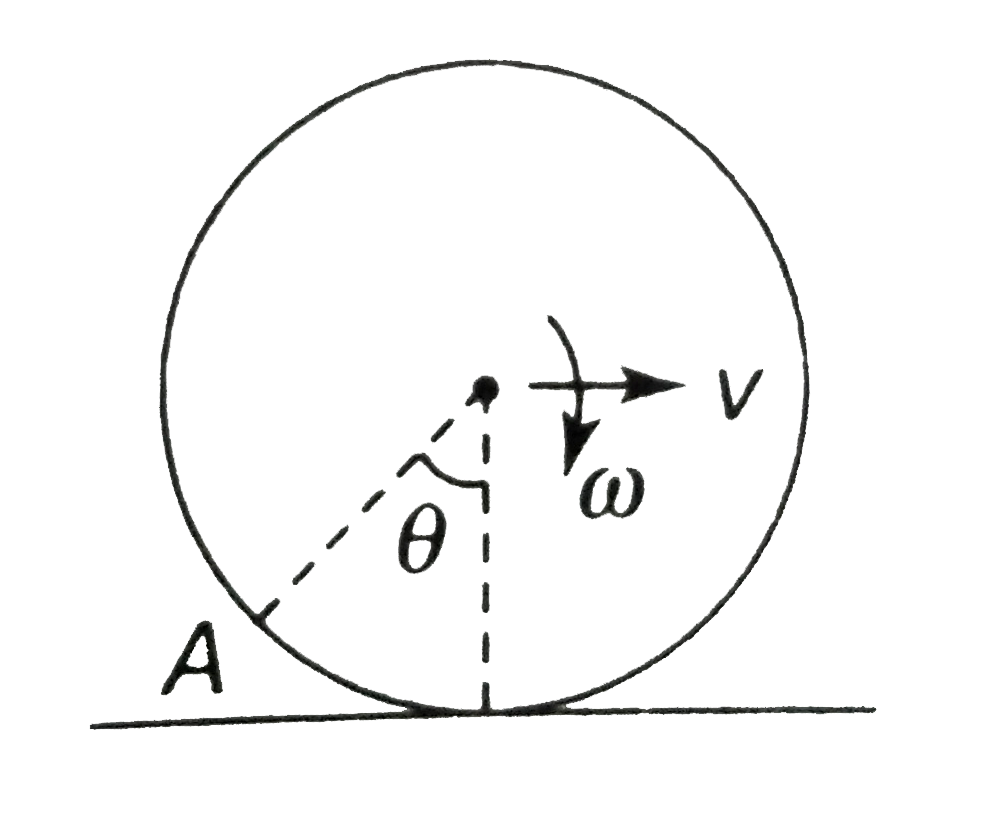
() When the point has rotated an angle , its velocity can be calculated in the following manner:

() Assuming rolling without slipping about the center of mass
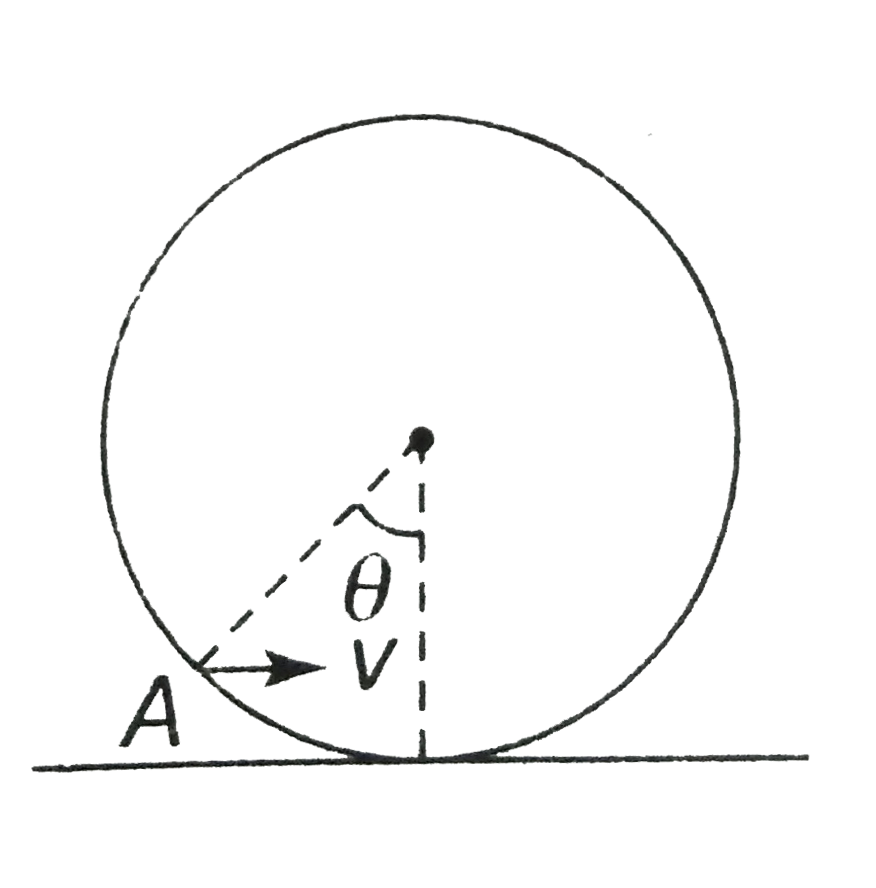


Alternatively the velocity of point can be calculated as follows.
() Rolling without slipping about the center of mass is equivalent to pure rotation about the contact point of wheel and surface

By the sine rule
Distance traveled in small time
Total distance travelved in one rotation, i.e.
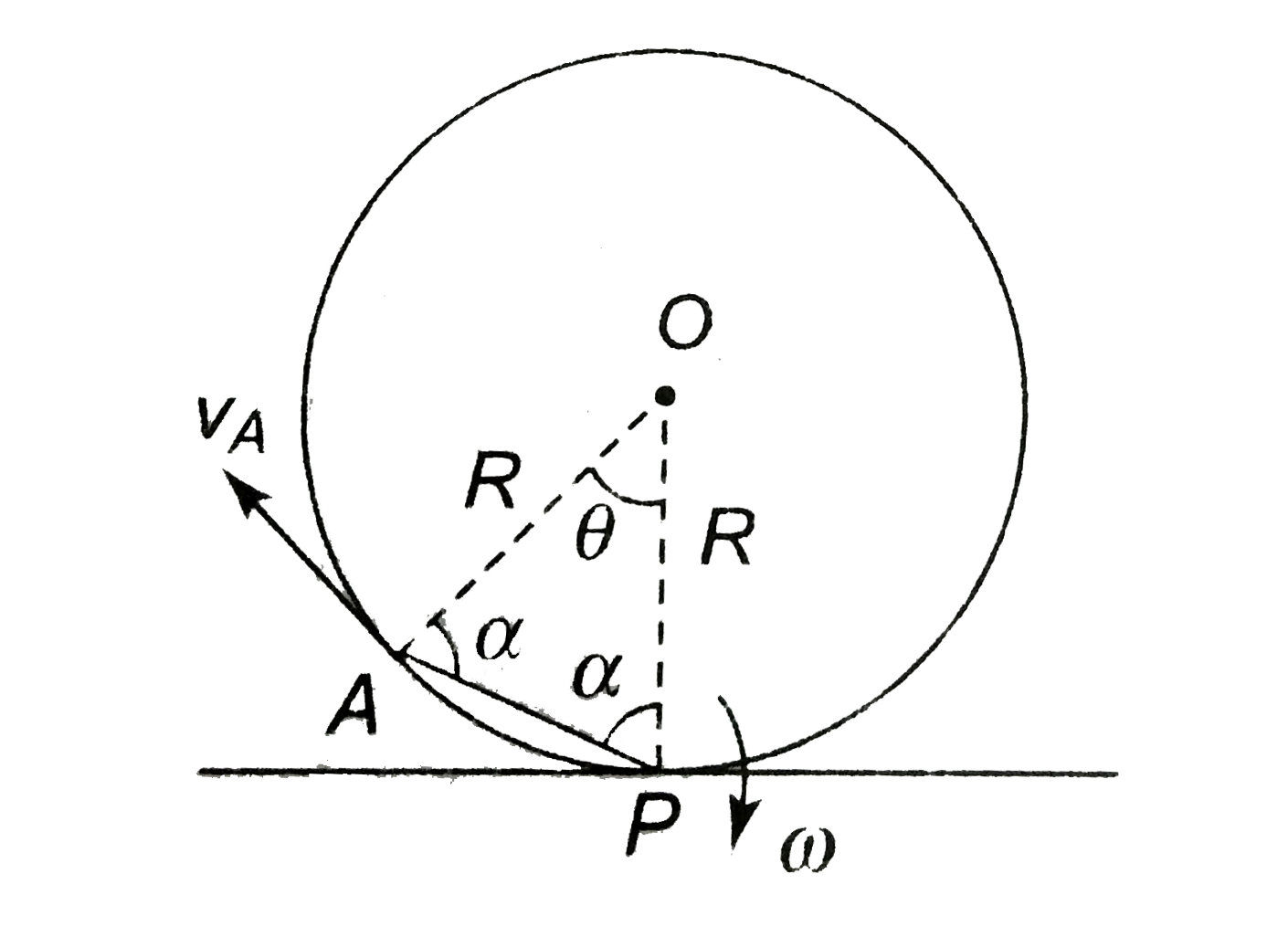
Distance

Topper's Solved these Questions
Similar Questions
A point A is located on the rim of a wheel of radius R which rolls witout slipping along a horizontal surface witih velocity V. Find the total distance traversed by the point A between successive moments at which it touches the surface.
View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0. We consider a point A on the surface of the disc. Then the acceleration of the point A is:
View Solution
Knowledge Check
- Question 1 - Select One
A points is A located on the rim of a wheel of radius R which rolls without slipping along a horizontal surface with velocity v. The total distance travelled by the point A between successive moments at which it touches the surface is :
A4RB2RC8RD√8R - Question 2 - Select One
A solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
AThe kinetic energy of rotation is 15mv20.BThe total kinetic energy is 710mv20.CThe mechanical energy (assume the ground as reference) is mgR+710mv20.DAll options are correct. - Question 3 - Select One
A solid sphere of mass 1 kg and radius 10 cm rolls without slipping on a horizontal surface, with a velocity of 20 cm/s. The total kinetic energy of the sphere is
A0.014 JB0.028 JC14 JD28 J
A circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0. We consider a point A on the surface of the disc. Then the acceleration of the point A is:
View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0 . We consider a point A on the surface of the disc. Then, the acceleration of point A is
View SolutionA disc rolls without slipping on a horizontal surface such that its velocity of center of the mass is v. Find the velocity of points A,B,C and D.
 View Solution
View SolutionA solid sphere of mass 1 kg and radius 10 cm rolls without slipping on a horizontal surface, with a velocity of 20 cm/s. The total kinetic energy of the sphere is
View SolutionA wheel rolls without slipping on a horizontal surface such that its velocity of center of mass is v. The velocity of a particle at the highest point of the rim is
View Solution

