A point charge Q is placed at the centre of circular disc of radius r . Calculate the electric flux associated with circular disc.
To solve the problem of calculating the electric flux associated with a circular disc when a point charge Q is placed at its center, we can follow these steps:
1. Understanding Electric Flux:
Electric flux (ΦE) through a surface is defined as the product of the electric field (E) and the area (A) of the surface, integrated over the surface. Mathematically, it is given by:
ΦE=∫→E⋅d→A
2. Identify the Geometry:
We have a circular disc of radius r with a point charge Q located at its center. The electric field produced by a point charge radiates outward in all directions.
3. Direction of Electric Field:
The electric field (→E) due to the point charge points radially outward from the charge. At the center of the disc, the electric field will be perpendicular to the surface of the disc.
4. Area Vector:
The area vector (d→A) for the circular disc points perpendicular to the surface of the disc.
5. Angle Between Electric Field and Area Vector:
Since the electric field lines are perpendicular to the area vector of the disc, the angle θ between the electric field vector and the area vector is 90∘.
6. Calculating the Electric Flux:
The electric flux can be calculated using the formula:
ΦE=E⋅A⋅cos(θ)
where θ=90∘. Thus, cos(90∘)=0.
7. Conclusion:
Since the cosine of 90∘ is zero, the electric flux through the circular disc is:
ΦE=E⋅A⋅0=0
Final Answer:
The electric flux associated with the circular disc is ΦE=0.
---
Electric flux (ΦE) through a surface is defined as the product of the electric field (E) and the area (A) of the surface, integrated over the surface. Mathematically, it is given by:
ΦE=∫→E⋅d→A
We have a circular disc of radius r with a point charge Q located at its center. The electric field produced by a point charge radiates outward in all directions.
The electric field (→E) due to the point charge points radially outward from the charge. At the center of the disc, the electric field will be perpendicular to the surface of the disc.
The area vector (d→A) for the circular disc points perpendicular to the surface of the disc.
Since the electric field lines are perpendicular to the area vector of the disc, the angle θ between the electric field vector and the area vector is 90∘.
The electric flux can be calculated using the formula:
ΦE=E⋅A⋅cos(θ)
where θ=90∘. Thus, cos(90∘)=0.
Since the cosine of 90∘ is zero, the electric flux through the circular disc is:
ΦE=E⋅A⋅0=0
The electric flux associated with the circular disc is ΦE=0.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Practice Problems
88 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Conceptual Questions
51 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
14 Videos
Similar Questions
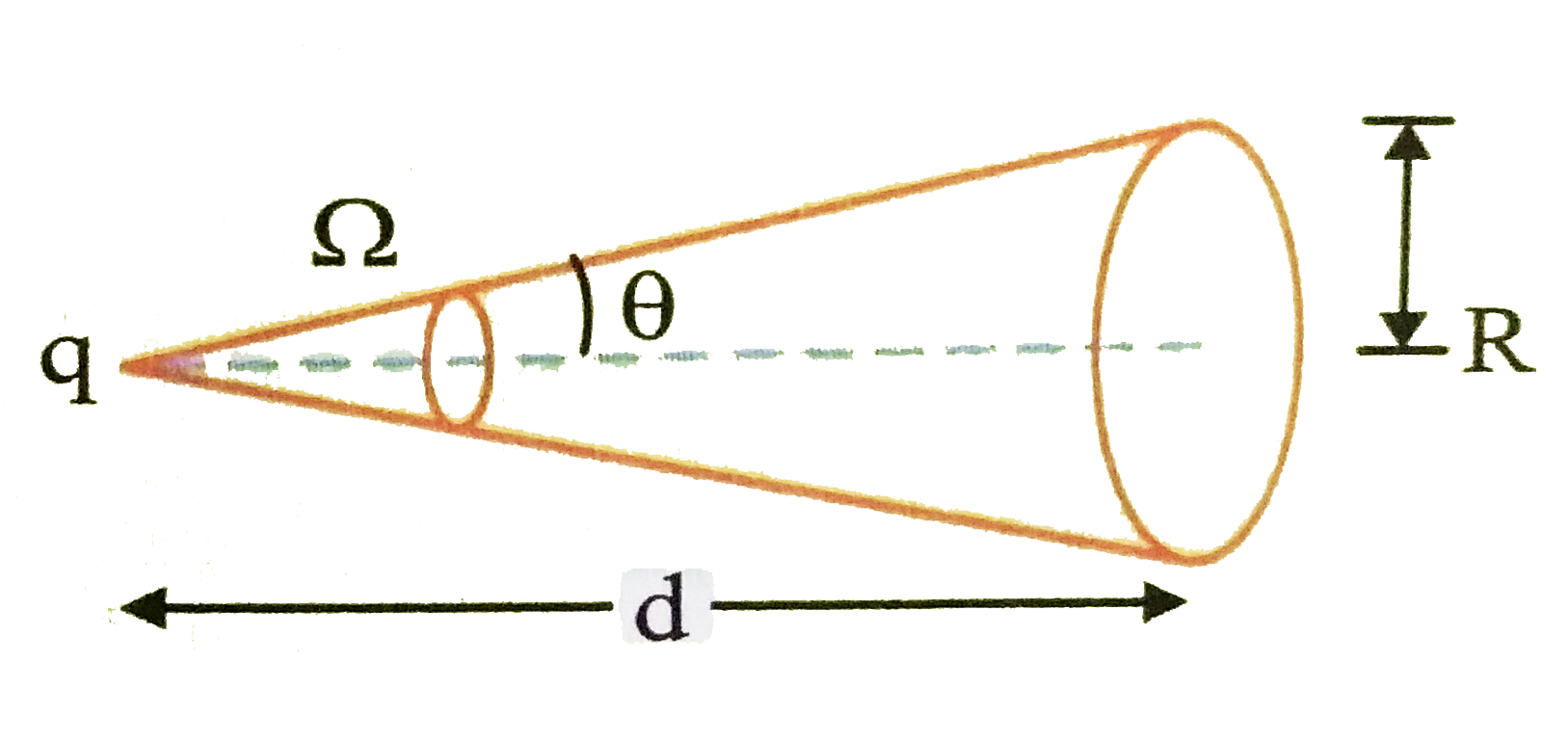
A point charge q is placed at a distance d form the center of circular disc of radius R. Find electric flux through the disc due to that charge
View SolutionA point charge Q is placed at the centre of a circular wire of radius R having charge q. Find the force of electrostatic interaction between point charge and the wire.
View Solution
Knowledge Check
a point charge q is placed at the centre of a cylinder of length L and radius R the electric flux through the curved surface of the cylinder is
Aqε0L√L2+R2Bqε0L√L2+2R2Cqε0L√L2+4R2Dq2ε0A charge 'Q' is placed at the centre of a hemispherical surface of radius 'R'. The flux of electric field due to charge 'Q' through the surface of hemisphere is
AQ/4ε0BQ/4πε0CQ/2ε0DQ/2πε0A position charge Q is placed at a distance of 4R above the centre of a disc of radius R. The magnitude of flux through the disc is ϕ. Now a hemispherical shell of radius R is placed over the disc such that it forms a closed surface. The flux through the curved surface (taking direction of area vector along outward normal as positive), is -
 AzeroBϕC−ϕD2ϕ
AzeroBϕC−ϕD2ϕ
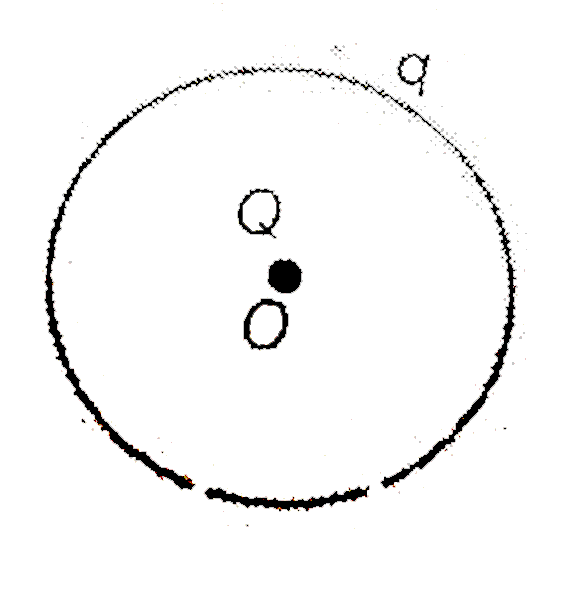
Point charge Q is placed at point P in the plane of circular face of sphere. The electric flux passing through the spherical part shown in the figure is:-
View SolutionA point charge +Q is placed at a point. Calculate the electric flux associated with one sphere of radius r , which the given point charge at its centre.
View SolutionA charge q is placed at the centre of a hollow sphere of radius r, Total electric flux passing through the spherical surface is __________
View SolutionA charge q is placed at the centre of a cylinder of radius R and length 2R. Then electric flux through the curved surface of the cylinder is
View SolutionThe angular velocity of circular disc of radius 2cm is 20 rad s−1. Calculate the linear velocity of the disc.
View Solution
