A point initially at rest moves along x-axis. Its acceleration varies with time as a=(6t+5)m/s2. If it starts from origin, the distance covered in 2 s is:
20m
18m
16m
25m
The correct Answer is:B
To solve the problem step by step, we will follow the process of integrating the acceleration to find the velocity and then integrating the velocity to find the distance.
Step 1: Write down the acceleration equation
The acceleration of the point is given by:
a(t)=6t+5m/s2
Step 2: Relate acceleration to velocity
We know that acceleration is the derivative of velocity with respect to time:
a=dvdt
Thus, we can write:
dvdt=6t+5
Step 3: Integrate to find velocity
To find the velocity, we integrate both sides with respect to time t:
∫dv=∫(6t+5)dt
This gives us:
v=3t2+5t+C
Since the point starts from rest, the initial velocity v(0)=0. Therefore, we can find the constant C:
0=3(0)2+5(0)+C⇒C=0
Thus, the velocity equation simplifies to:
v(t)=3t2+5t
Step 4: Relate velocity to distance
Now, we know that velocity is the derivative of distance with respect to time:
v=dsdt
So we can write:
dsdt=3t2+5t
Step 5: Integrate to find distance
We integrate both sides with respect to time t:
∫ds=∫(3t2+5t)dt
This gives us:
s=t3+52t2+C′
Again, since the point starts from the origin, the initial distance s(0)=0. Therefore, we find the constant C′:
0=(0)3+52(0)2+C′⇒C′=0
Thus, the distance equation simplifies to:
s(t)=t3+52t2
Step 6: Calculate distance at t=2 seconds
Now, we substitute t=2 seconds into the distance equation:
s(2)=(2)3+52(2)2
Calculating this gives:
s(2)=8+52⋅4
s(2)=8+10=18meters
Final Answer
The distance covered in 2 seconds is:
18meters
---
The acceleration of the point is given by:
a(t)=6t+5m/s2
We know that acceleration is the derivative of velocity with respect to time:
a=dvdt
Thus, we can write:
dvdt=6t+5
To find the velocity, we integrate both sides with respect to time t:
∫dv=∫(6t+5)dt
v=3t2+5t+C
Since the point starts from rest, the initial velocity v(0)=0. Therefore, we can find the constant C:
0=3(0)2+5(0)+C⇒C=0
Thus, the velocity equation simplifies to:
v(t)=3t2+5t
Now, we know that velocity is the derivative of distance with respect to time:
v=dsdt
So we can write:
dsdt=3t2+5t
We integrate both sides with respect to time t:
∫ds=∫(3t2+5t)dt
s=t3+52t2+C′
Again, since the point starts from the origin, the initial distance s(0)=0. Therefore, we find the constant C′:
0=(0)3+52(0)2+C′⇒C′=0
Thus, the distance equation simplifies to:
s(t)=t3+52t2
Now, we substitute t=2 seconds into the distance equation:
s(2)=(2)3+52(2)2
Calculating this gives:
s(2)=8+52⋅4
s(2)=8+10=18meters
The distance covered in 2 seconds is:
18meters
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Assertion and reason)19videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Mathch the columns)6videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.715videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrances gallery19videos
MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective10videos
PROJECTILE MOTION
Similar Questions
A particle of mass 200gm is moving in a circular path of radius 10cm, such that its tangential acceleration varies with time as at=6t (m/s2) . The average power delivered to the particle by force acting on it in the first 10sec is 100K watt. The particle starts from rest. Find K.
View SolutionA particle moves along x-axis such that its position veries with time as x=50t−5t2. Select the correct alternative (s).
View Solution
Knowledge Check
- Question 1 - Select One
A body starts from rest and moves with a uniform acceleration. The ratio of the distance covered in the nth sec to the distance covered in n sec is
A2n−1n2B1n2−1nC2n2−1n2D2n+1n2
A particle starts from rest. Its acceleration is varying with time as shown in the figure. When the particle comes to rest, its distance from its starting point is
 View Solution
View SolutionA particle moves along the x-axis in such a way that its x-co-ordinate varies with time as x=2–5t+6t2.
The initial velocity and acceleration of particle will respectively be-View SolutionA body, initially at rest, starts moving with a constant acceleration 2 ms−2. Calculate : (i) the velocity acquired and (ii) the distance travelled in 5 s.
View SolutionA particle, initially at rest, starts moving in a straight line with an acceleration a=6t+4m/s2. The distance covered by it in 3 s is
View SolutionA particle moves aling x-axis with an initial speed v0=5ms−1. If its acceleration varies with with time asshown in a−t graph in .
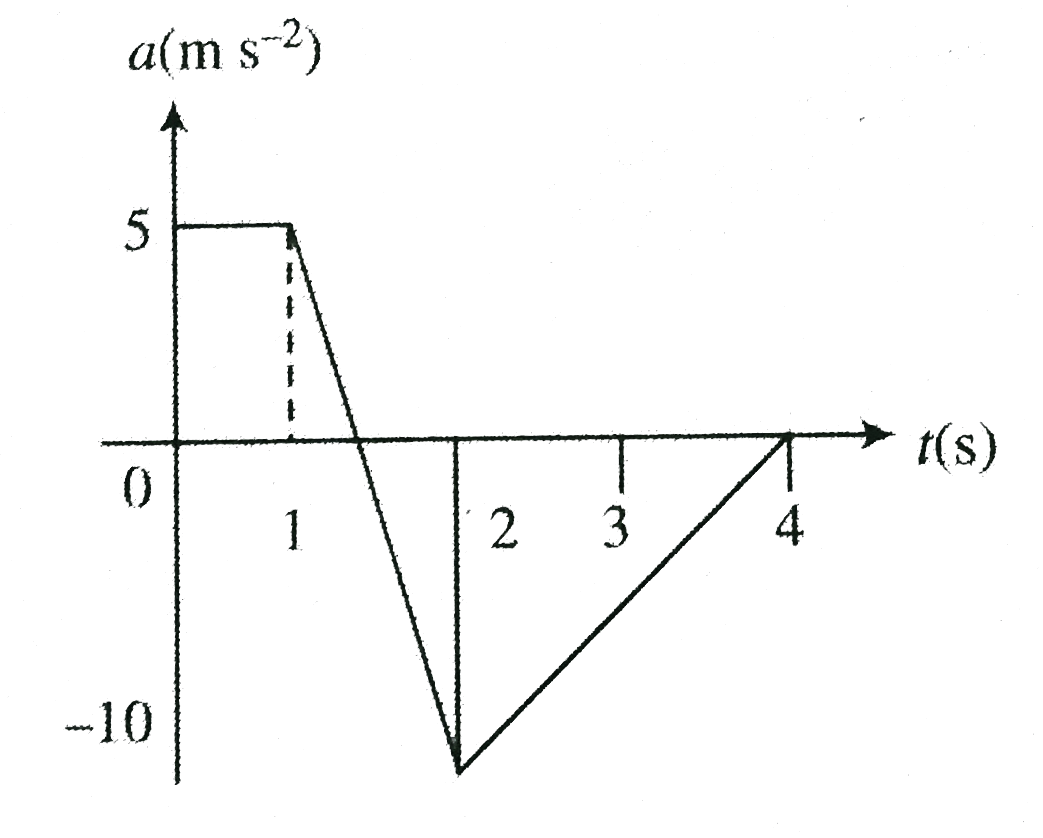 .
.
a. Find the time when the particle starts moving along - x directionView SolutionA particle is moving along the x-axis with an acceleration a = 2x where a is in ms–2andx is in metre. If the particle starts from rest at x=1 m, find its velocity when it reaches the position x = 3.
View SolutionA particle is moving along x-axis. Its X-coordinate varies with time as, X=2t2+4t−6 Here, X is in metres and t in seconds. Find average velocity between the time interval t=0→t=2s.
View Solution
